Mathematical modeling - linear programming

Catalog

Basic concepts

Model solving and application

Solver based solution method

Problem based solution

other  

---

Basic concepts

An important branch of operations research is mathematical programming , Linear programming is an important branch of mathematical programming .

Variables are called The decision variables , The goal of the plan is called Objective function , The restriction is called constraint condition ,s.t. yes “ Bound ” It means .

The general steps of establishing a linear programming model are ：① To analyze problems , Find out the decision variables .② Find equality or inequality constraints .③ Construct a linear function about decision variables .

General form of linear programming model ：

or ：

Is the coefficient vector of the objective function , Also called value vector ; Is the decision vector ; Is the coefficient matrix of the constrained equations ; Is the constant vector of the constrained equations .

And standard ：

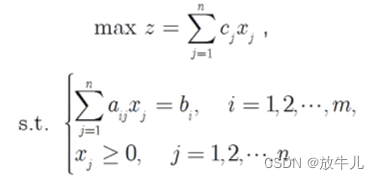
The objective function is very large , The constraints are equality constraints . The solution satisfying the constraint conditions is a feasible solution , Making the objective function reach the maximum value is called the optimal solution . The set of all feasible solutions is called feasible region , Write it down as R.

In the process of solving mathematical programming problems , Be sure to calculate Sensitivity analysis . Sensitivity analysis refers to the analysis of the sensitivity of the system due to changes in surrounding conditions . For linear programming problems a、b、c Are set to constant , But in practice , These coefficients will change a little .

Model solving and application

MATLAB There are two models for solving mathematical programming problems in ： Solver based solution method and Problem based solution ,

Solver based solution method

It is necessary to convert linear programming into standard form ：

The objective function must be minimized , Constraints are divided into less than or equal to constraints and equal sign constraints ,lb and ub Is the upper and lower bounds of decision variables .

MATLAB The function call format is ：

[x,fval] = linprog(f,A,b)

[x,fval] = linprog(f,A,b,Aeq,beq)

[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub)

x Returns the value of the decision variable ,fval It returns the optimal value of the objective function ,f It's the value vector ,A,b Corresponding to the linear inequality constraint ,Aeq and beq Corresponding to the constraints of linear equality ,lb and ub Corresponding to the lower bound vector and the upper bound vector of the decision vector respectively .

This method can only be applied to The decision vector is one-dimensional The situation of .

Problem based solution

First, the optimization problem is constructed with variables and expressions , And then use solve Function solving , It can be used doc optimproblem view help .

①prob=optimproblem('ObjectiveSense','max');

ObjectiveSense It can be max and min, Represents the maximum or minimum value of optimization , The default is min

② Definition f,A,b（ ditto ,f Can be defined as a row vector , In this way, the objective function is different and then transposed ）

③x=optimvar('x',2,1,'TYPE','integer','LowerBound',0,'UpperBound',inf);

first ‘x’ Inside is the variable name , Column vector , Then there are several rows and columns .

‘TYPE’, What is defined later is the type of the function , for instance integer Integer type ,double Double precision models

‘LowerBound' And 'UpperBound' Indicates what the lower and upper bounds follow 0,inf They are the scope

④prob.Objective=f * x;% Objective function , The objective function needs to get a scalar value , Not a matrix vector

⑤prob.Constraints.con=A*x<=b;% constraint condition , There is only one constraint , Or you can skip it .con,.con Is the label , You can name it yourself , When there are multiple constraints , Must label cannot be the same .

⑥[sol fval flag out]=solve(prob);%fval It's the best value ,sol.x Is the value of the decision variable , When there are multiple decision variables , Sure sol.y,flag Don't worry about in linear programming , Note that it cannot be negative in nonlinear programming .

for example ：

  Use solver to solve ：

clc,clear
f = [-2;-3;5];% To find the minimum 
A = [-2,5,-1;1,3,1];
b = [-10;12];
Aeq = [1,1,1];
beq = [7];
lb = zeros(3,1);
[x,fval] = linprog(f,A,b,Aeq,beq,lb,[]);
x
-fval

x =

    6.4286
    0.5714
         0
ans =

   14.5714

Use problem-based solutions

clc,clear
prob=optimproblem('ObjectiveSense','max');
x=optimvar('x',3,'LowerBound',0);
prob.Objective=2*x(1) + 3*x(2) - 5*x(3);
prob.Constraints.con1=2*x(1) - 5*x(2) + x(3)>=10;
prob.Constraints.con2=x(1) + 3*x(2) + x(3)<=12;
prob.Constraints.con3=x(1) + x(2) + x(3)==7;
[sol fval flag out]=solve(prob);
sol.x
fval

ans =

    6.4286
    0.5714
         0
fval =

   14.5714

other  

• MATLAB in , Load existing txt Matrix of documents , If use load function , Then the number of rows and columns of the matrix should be equal . If individual numbers are missing , You can use readmatrix function .writematrix(a,'data.xlsx') Can write Excel in . 
• Matrix index a(1:end,1),end It is automatically the last column of the row
• sum(a,'all') According to matrix a The sum of all the elements of