15 -- 最接近原点的 K 个点

题目

Github链接
最接近原点的 K 个点

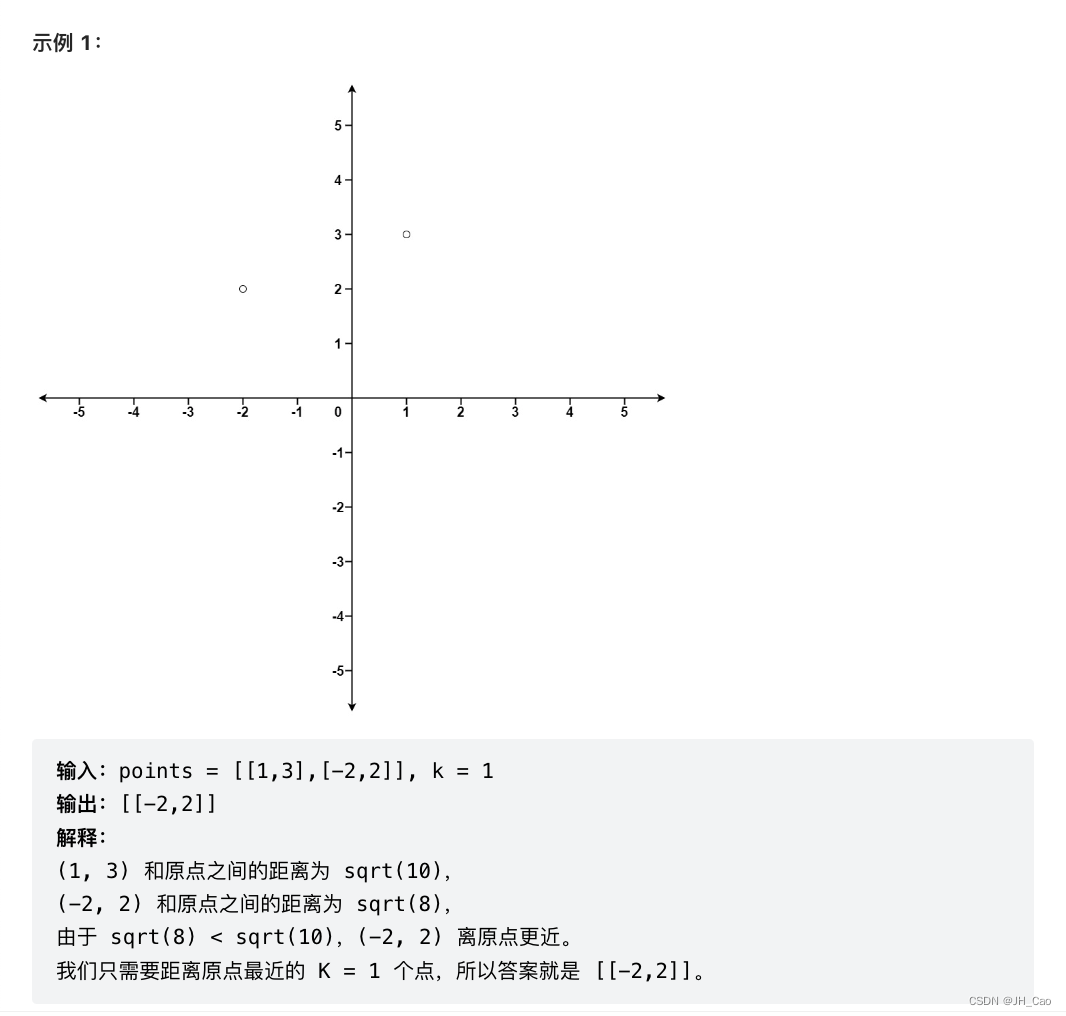
给定一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点，并且是一个整数 k ，返回离原点 (0,0) 最近的 k 个点。

这里，平面上两点之间的距离是 欧几里德距离（ √(x1 - x2)2 + (y1 - y2)2 ）。

你可以按 任何顺序 返回答案。除了点坐标的顺序之外，答案 确保 是 唯一 的。

• 思路

1. 当然你可以进行排序，再求前面K个数
2. 但是这题考察的主要是建堆，这是经典的topK问题，一想到topK问题，就要想到建堆
3. 那么问题来了，建小顶堆还是大顶堆呢？
4. 先记住口诀：

topK小，大顶堆；topK大，小顶堆

5. 为什么会是这样呢？
   （1）因为求topK小的时候，建大顶堆，堆顶元素的是这个topK小里面的最大元素，这样方便后面的元素来进行比较；

   比如说，[2,4,6,5,1]中，求前top3小的值
   建大顶堆，堆的长度为3
   容易得出：堆顶为6，左为2， 右为4,
   当前堆即为 :[6,2,4]
   当新的元素5进来建堆，比较的时候
   先拿出堆顶元素6来比较，发现6比5大，
   （a）那么添加到数组中得到: [6,2,4,5]
   （b）然后交换数组首尾元素，得到: [5,2,4,6]
   （c）再删除最后一个元素,得到: [5,2,4]
   这就是最新的堆，以此类推
   （d）当1来进行建堆的时候，得到: [1,2,4]
   到此结束，得出top3小的元素就是 [1,2,4]

(2)求topK大，建小顶堆，原理和上述类似。

• 答案
• 本题的代码：

class facebook03 {
    // 求距离最小的topK,建大顶堆
    // 堆的堆顶元素,是topK的最后一个,也就是说,后面的值,比较,只需要和最顶端的元素进行比较
    // 这就是为什么说,求topK小,建大顶堆
    // 反过来说,如果求topK大,就建小顶堆
    // 总结记忆口诀: topK大,小顶堆;topK小,大顶堆
    
    var lock = NSLock()
    func kClosest(_ points: [[Int]], _ k: Int) -> [[Int]] {
        let heap = MyHeap(k)
        
        for i in 0..<points.count {
            let curPoint = points[i]
            lock.lock()
            let val = helper(curPoint) //[[6,10],[-3,3],[-2,5],[0,2]]
            print(i,"--",val)
            heap.createHeap([i: val])
            lock.unlock()
        }
        
        var res = [[Int]]()
        
        for i in 0..<k {
            let ele = heap.heapArr[i]
            let index = ele.first!.key
            res.append(points[index])
        }
        
        return res
    }
    
    func helper(_ p:[Int]) -> Int {
        return p[0] * p[0] + p[1] * p[1]
    }
}

class MyHeap {
    var heapArr = [[Int: Int]]()
    var topK: Int!
    init(_ top: Int) {
        topK = top
    }
    

    func createHeap(_ dict: [Int: Int]) {
        if heapArr.count < topK {
            heapArr.append(dict)
            siftUp(heapArr.count - 1)
        } else {
            if !compare(dict, heapArr[0]) {
                heapArr.append(dict)
                heapArr.swapAt(0, heapArr.count - 1)
                heapArr.removeLast()
                siftDown(0)
            }
        }
    }
    
    private func siftUp(_ index: Int) {
        if index < 1 {
            return
        }
        let parent = (index - 1) / 2
        if compare(heapArr[index], heapArr[parent]) {
            heapArr.swapAt(parent, index)
            siftUp(parent)
        }
        
    }
    
    private func siftDown(_ index: Int) {
        var left = index * 2 + 1
        var right = index * 2 + 2
        var parent = index
        
        if left < heapArr.count && !compare(heapArr[parent], heapArr[left]) {
            swap(&parent, &left)
        }
        
        if right < heapArr.count && !compare(heapArr[parent], heapArr[right]) {
            swap(&parent, &right)
        }
        
        if parent != index {
            heapArr.swapAt(parent, index)
            siftDown(parent)
        }
    }
    
    private func compare(_ ele1: [Int: Int], _ ele2: [Int: Int]) -> Bool {
        
        if ele1.first!.value > ele2.first!.value {
            return true
        } else {
            return false
        }
    }
    
}