当前位置:网站首页>[training Day8] [luogu_p6335] staza [tarjan]
[training Day8] [luogu_p6335] staza [tarjan]
2022-07-24 20:10:00 【VL——MOESR】

Ideas :
We set up fi Indicates the current downward link , Walk back i Maximum path to
gi It means going down at the current point , Don't walk back i Maximum path to
set up w=gi-fi, that gi=fi+w
If i To j The side of is not in the ring , That obviously won't be right fi Contribute to , So let's finish everything first fi, Then go down gj, therefore w=gi+fi+1-fi, Take all the maximum
Then if i To j It's in the ring , Then go through every point in the ring first , Put their f All finished ( This is obviously the biggest ), Contribution: u. Then set v It means that you go to a certain point in the process of walking and don't continue , Instead, it's the one who walks it g, be v=max(dis(i,j)+ ∑ k f k + g j \sum_{k}f_k+g_j ∑kfk+gj),j At which point do you stay ,k yes i Go to the j All passing points . Attention from i To j There are two directions , So we have to calculate . therefore w=max(v-u).
The final answer is g1
c o d e code code
#include<iostream>
#include<cstdio>
using namespace std;
const int MAXN = 1e5 + 10;
int n, m;
int cnt, dfn[MAXN], low[MAXN], f[MAXN], g[MAXN], fa[MAXN];
int tot, head[MAXN];
struct node {
int to, next;
}b[MAXN * 2];
void add(int x, int y) {
b[++ tot] = (node) {
y, head[x] };
head[x] = tot;
}
void tarjan(int x) {
dfn[x] = low[x] = ++ cnt;
int w = 0;
for(int i = head[x]; i; i = b[i].next) {
int y = b[i].to;
if(y == fa[x]) continue;
if(!dfn[y]) {
fa[y] = x;
tarjan(y);
low[x] = min(low[y], low[x]);
if(low[y] > dfn[x]) w = max(w, g[y] + 1);
}
else low[x] = min(low[x], dfn[y]);
}
for(int i = head[x]; i; i = b[i].next) {
int y = b[i].to;
if(dfn[y] > dfn[x] && fa[y] != x) {
int u = 1, v = 0;
for(int k = y; k != x; k = fa[k])
v = max(v, u + g[k]), u += f[k] + 1;
f[x] += u;
int tmp = u;
for(int k = y; k != x; k = fa[k])
tmp -= f[k] + 1, v = max(v, tmp + g[k]);
w = max(w, v - u);
}
}
g[x] = w + f[x];
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; i ++) {
int x, y;
scanf("%d%d", &x, &y);
add(x, y), add(y, x);
}
tarjan(1);
printf("%d", g[1]);
return 0;
}
边栏推荐
- Sql164 next day retention rate of new users per day in November 2021
- What is IDE (integrated development environment)
- Detailed explanation of ELF format (I)
- Valdo2021 - vascular space segmentation in vascular disease detection challenge (2)
- Virtual machine win7 system installation vmtool
- (posted) differences and connections between beanfactory and factorybean
- Richview table table alignment
- 02 | environment preparation: how to install and configure a basic PHP development environment under windows?
- Setting up a dual machine debugging environment for drive development (vs2017)
- VLAN Technology
猜你喜欢

How to use the interface control telerik UI for WinForms development step progress bar?

Istio二之流量劫持过程

English grammar_ Demonstrative pronoun this / these / that / those

C form application treeview control use
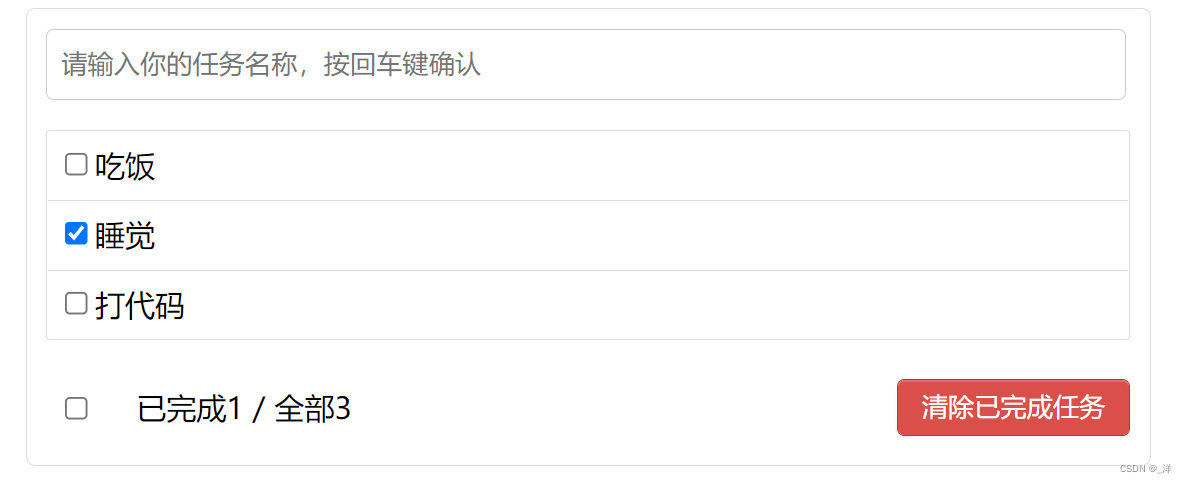
Todolist case

The U.S. economy continues to be weak, and Microsoft has frozen recruitment: the cloud business and security software departments have become the hardest hit

Substr and substring function usage in SQL

Look at the interface control devaxpress WinForms - how to customize auxiliary function properties (Part 2)
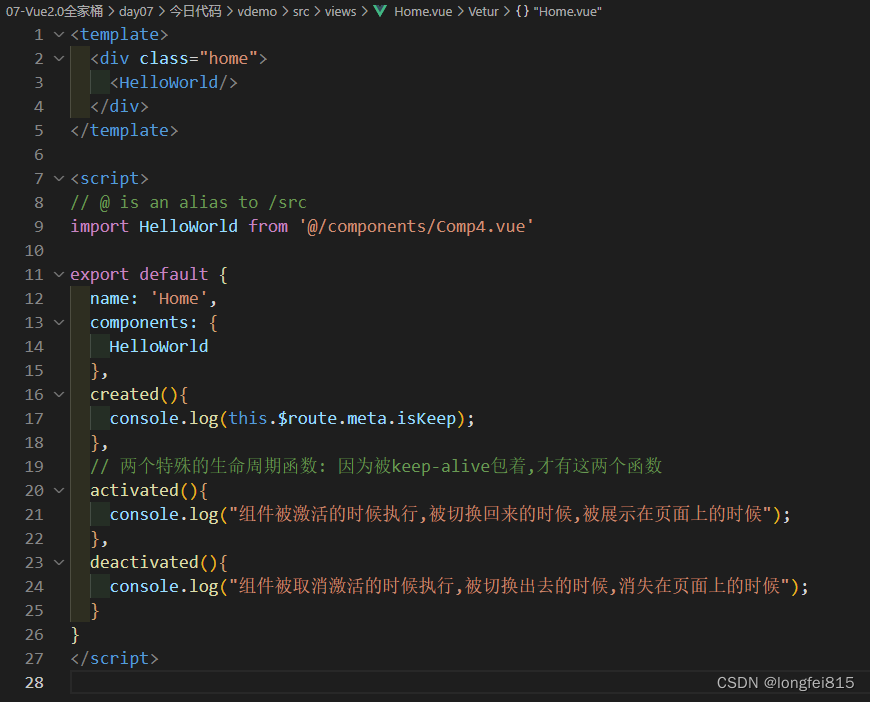
147 set whether to cache by using the routing meta information - use of include and exclude - use of activated and deactivated

Are network security and data security indistinguishable? Why is data security important?
随机推荐
VLAN Technology
Lights of thousands of families in the year of xinchou
Create a life cycle aware MVP architecture
Redisgraph graphic database multi activity design scheme
C # shelling tool for code encryption protection
Guys, I have no problem running locally in diea, running on the server. What's wrong with the lack of CDC connection? The database IP can be pinged
The beginning of winter in the year of bitterness and ugliness
Connect the smart WiFi remote control in the home assistant
Using videoview to realize video playback in turns
Actual measurement of Qunhui 71000 Gigabit Network
01 | 开篇词:手把手教你搭建一个博客网站
Maya coffee machine modeling
Expression evaluation (stack)
Thymeleaf application notes
MySQL advanced
Framework API online viewing source code
Make Huawei router into FTP server (realize upload and download function)
Solve the problem that gd32f207 serial port can receive but send 00
Classic interview questions of interface testing: what is the difference between session, cookie and token?
Implementation of OA office system based on JSP