【贝叶斯分类4】贝叶斯网

1. 半朴素贝叶斯分类器知识回顾

  半朴素贝叶斯分类器的原理就是适当考虑一部分属性间的依赖信息。考虑策略最常用的是独依赖估计，有超夫独依赖估计（SPODE）,平均独依赖估计（AODE）,树增广朴素贝叶斯（TAN）。
  
  超夫独依赖估计就是直接让所有属性都依赖同一个属性，这个被其他属性共同依赖的叫“超夫”，超夫选择不是一直是它，可以用交叉验证的方法，我们选择最好训练效果的模型。
  
  平均独依赖估计是把每个属性当作一个SPODE模型，但$P(c)$ 变为了$P(c,x_i)$，但这个模型要求训练集足够大，定义一个阈值$m^{\prime }$，要求$|D_{x_i}|\ge m^{\prime }$。
  
  树增广朴素贝叶斯，基于最大带权生成树算法，算两两属性间的条件互信息，$I(x_i,x_j|y)$ 越大，代表依赖越强。

2. 贝叶斯网学习笔记

2.1 引言

  贝叶斯网亦称“信念网”，它借助有向无环图来刻画属性之间的依赖关系，并使用条件概率表来描述属性的联合概率分布，是一种概率图模型，帮助人们将概率统计应用于复杂领域，进行不确定推理和数值分析的工具。

  贝叶斯网络是从条件概率的角度描述变量之间依赖关系的有向无环图（DAG）。揭示变量之间的依赖关系，也作因果关系（是贝叶斯网的特点），它模拟了人类推理过程中因果关系的不确定性。

2.2 知识卡片

	1. 贝叶斯网络：Bayesian Network，简称BN
	2. 信念网：belief network
	3. 条件概率表：Conditional Probability Table，简称CPT
	4. 因果关系
	5. 有向无环图：Directed Acyclic Graph，简称DAG

2.3 概率图模型(PGM)

2.3.1 引言

  概率图模型（Probabilistic Graphical Model），结合概率论和图论，是指一种用图结构来描述多元随机变量之间条件独立性的概率模型（注意条件独立性），从而给研究高维空间的概率模型带来了很大的便捷性。分为贝叶斯网络和马尔可夫网络两大类。
  
  我们希望能够挖掘隐含在数据中的知识，概率图构建了这样一个图。概率图直观地表示随机变量间条件独立性的关系。

2.3.2 为什么引入概率图?

  高阶变量（k 维随机变量），$Y=[X_1,X_2,...,X_k]$，假设每个随机变量为离散型，取值有$m$ 个。那么在不作任何独立性条件下，则需要$m^k-1$ 个参数才能表示其概率分布，参数是指数级的。
  
  而一种有效减少参数量的方法就是独立性假设。首先将k维随机变量的联合概率分解为k个条件概率的乘积，那么$P(y)={\prod }_{k=1}^{k}P(x_k|x_1,x_2,...,x_{k-1})$。如果两个变量独立，则条件概率的条件将减少。
  
  例：已知$X_1$ 时，$X_2$ 和$X_3$ 独立，$X_1$ 和$X_4$ 独立. 则$P(x_2|x_1,x_3)=P(x_2|x_1)$，$P(x_3|x_1,x_2)=P(x_3|x_1)$。则联合概率$P(y)=P(x_1)P(x_2|x_1)P(x_3|x_1)P(x_4|x_2,x_3)$。

2.3.3 概率图的三个基本问题（表示，学习，推断）

1. 表示问题：对于一个概率模型，如何通过图结构来描述变量之间的依赖关系。
2. 学习问题：图模型的学习包括图结构的学习和参数的学习。
3. 推断问题：在已知部分变量时，计算其他变量的条件概率分布。

2.4 贝叶斯网

2.4.1 贝叶斯网的表达

• 组成

  一个贝叶斯网$B$ 由结构$G$ 和参数$\theta$ 两部分构成，即$B=<G,\theta >$. 网络结构$G$ 是一个有向无环图，其每个节点对应于一个属性。若两个属性有直接依赖关系，则它们由一条边连接起来；参数$\theta$ 定量描述这种依赖关系。假设属性$x_i$ 在$G$ 中的父节点集为${\pi }_i$，则$\theta$ 包含了每个属性的条件概率表${\theta }_{x_i|{\pi }_i}=P_B(x_i|{\pi }_i)$

• 例子

  从图中网络结构可看出，“色泽” 直接依赖于 “好瓜 “和"甜度”，而"根蒂"则直接依赖于"甜度”，“敲声"直接依赖于"好瓜”。进一步从条件概率表能得到"根蒂"对"甜度"量化依赖关系，如P(根蒂=蜷缩|甜度=高)=0.9.

2.4.2 结构

2.4.2.1 联合概率分布

  离散性随机变量的联合概率分布，贝叶斯网结构有效地表达了属性间的条件独立性。给定父节点集${\pi }_i$，贝叶斯网假设每个属性与它的非后裔属性独立，于是$B=<D,\theta >$ 将属性$x_1,x_2,...,x_d$ 的联合概率分布定义为：
$$P_B(x_1,x_2,...,x_d)=\prod _{i=1}^d{P}_B(x_i|{\pi }_i)=\prod _{i=1}^d{\theta }_{x_i|{\pi }_i}$$

2.4.2.2 属性独立的记法

$$x_3和x_4在给定x_1的取值时独立:x_3\perp x_4|x_1$$

2.4.2.3 贝叶斯网中三个变量典型的依赖关系

1. 同父结构
   给定父结点$x_1$ 的取值，则$x_3$ 与$x_4$ 条件独立。

2. V型结构
   给定子结点$x_4$ 的取值，$x_1$ 与$x_2$ 必不独立。
   若$x_4$ 的取值完全未知，但$x_1$ 与$x_2$ 却是相互独立的。

3. 顺序结构
   给定$x$ 的值，则$y$ 与$z$ 条件独立。

2.4.2.4 道德图

【引言】
  "道德化"的蕴义:孩子的父母应建立牢靠的关系，否则是不道德的。

  为了分析有向图中变量间的条件独立性，可使用“有向分离”，把有向图转变为一个无向图，此时产生的无向图称为道德图。基于道德图能直观、迅速地找到变量间的条件独立性。

【步骤】

1. 找出有向图中的所有V型结构，在V型结构的两个父结点之间加上一条无向边;
2. 将所有有向边改为无向边。

【原理】
  假定道德图中有变量$x,y$ 和变量集合$z=\{z_i\}$，若变量$x$ 和$y$ 能够在图上被$z$ 分开，即从道德图中将变量集合$z$ 去除后（删除结点及关联边），$x$ 和$y$ 分属两个连通分支，则称变量$x$ 和$y$ 被$z$ 有向分离，$x\perp y|z$ 成立。

【例子】

道德化

$x_3\perp x_2|x_1$

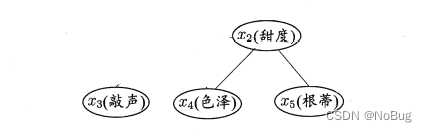
2.4.3 学习

2.4.3.1 任务

  若网络结构己知，即属性间的依赖关系己知，则贝叶斯网的学习过程相对简单，只需通过对训练样本"计数"，估计出每个结点的条件概率表即可。

  但在现实应用中我们往往并不知晓网络结构。于是，贝叶斯网学习的首要任务就是根据训练数据集来找出结构最"恰当"的贝叶斯网。

2.4.3.2 评分搜索

  "评分搜索"是求解这一问题的常用办法。具体来说，我们先定义一个评分函数(score function) ，以此来评估贝叶斯网与训练数据的契合程度，然后基于这个评分函数来寻找结构最优的贝叶斯网。

2.4.3.3 评分函数

• 准则一：最小描述长度准则

  最小描述长度准则（Minimal Description Length, 简称MDL准则），学习的目标是找到一个能以最短编码长度描述训练数据的模型，此时编码的长度包括了描述模型自身所需的字节长度和使用该模型描述数据所需的字节长度（编码的长度=描述模型自身所需的字节长度+使用该模型描述数据所需的字节长度）。

• 准则一的应用，贝叶斯网

  给定训练集$D=\{x_1,x_2,...,x_m\}$，贝叶斯网$B=<G,\theta >$ 在$D$ 上的评分函数可写为：
$$s(B|D)=f(\theta )|B|-LL(B|D)$$
【其中】，

• |B| 是贝叶斯网的参数个数；
• $f(\theta )$ 是描述每个参数$\theta$ 所需的字节数；
• LL(B|D) 是贝叶斯网$B$ 的对数似然，$LL(B|D)={\sum }_{j=1}^{m}log{P}_B(x_j)$.

【显然】，

• $f(\theta )|B|$: 计算编码贝叶斯网$B$ 所需的字节数；
• $LL(B|D)$: 计算$B$ 所对应的概率分布$P_B$ 需要多少字节来描述D.

【因此】，

• 学习任务转化为一个优化任务。
• 寻找一个贝叶斯网$B$ 使评分函数$s(B|D)$ 最小。

【$f(\theta )$】，

• $f(\theta )=1$，即每个参数用1字节描述，得到AIC评分函数。
• $f(\theta )=\frac{1}{2}logm$，即每个参数用$\frac{1}{2}logm$字节描述，得到BIC评分函数。
• $f(\theta )=0$，则评分函数退化为负对数似然，相应的，学习任务退化为极大似然估计。

2.4.3.4 G固定，对参数$\theta$ 的极大似然估计

• 对偶转化

  $s(B|D)=f(\theta )|B|-LL(B|D)$，不难发现，若贝叶斯网$B=<G,\theta >$ 的网络结构$G$ 固定，则评分函数$s(B|D)$ 的第一项为常数，此时，最小化$s(B|D)$ 等价于对参数$\theta$ 的极大似然估计。$argmaxLL(B|D)$，因为$LL(B|D)={\sum }_{j=1}^{m}log{P}_B(x_j)$，$P_B(x_1,x_2,...,x_d)={\prod }_{i=1}^d{P}_B(x_i|{\pi }_i)={\prod }_{i=1}^d{\theta }_{x_i|{\pi }_i}$

• 参数计算公式

  这样参数${\theta }_{x_i|{\pi }_i}$能直接在训练数据D 上通过经验估计获得，即
$${\theta }_{x_i|{\pi }_i}={\hat{P}}_D(x_i|{\pi }_i)$$

• NP难问题

  因此，为了最小化评分函数$s(BID)$，只需对网络结构进行搜索，而候选结构的最优参数可直接在训练集上计算得到。不幸的是，从所有可能的网络结构空间搜索最优贝叶斯网结构是一个 NP难问题，难以快速求解。

• 解决

1. 第一种是贪心法，例如从某个网络结构出发，每次调整一条边(增加、删除或调整方向)，直到评分函数值不再降低为止。

2. 第二种是通过给网络结构施加约束来削减搜索空间，例如将网络结构限定为树形结构等。

2.4.4 推断

2.4.4.1 引言

  贝叶斯网训练好之后就能用来回答"查询" (query)，即通过一些属性变量的观测值来推测其他属性变量的取值。例如在西瓜问题中，若我们观测到西瓜色泽青绿、敲声烛响、根蒂蜷缩，想知道它是否成熟、甜度如何.这样通过已知变量观测值来推测待查询变量的过程称为"推断" (inference) ，己知变量观测值称为"证据" (evidence)。

  最理想的是直接根据贝叶斯网定义的联合概率分布来精确计算后验概率，不幸的是，这样的"精确推断"己被证明是 NP 难的。换言之，当网络结点较多、连接稠密时，难以进行精确推断，此时需借助"近似推断"，通过降低精度要求，在有限时间内求得近似解。

  在现实应用中，贝叶斯网的近似推断常使用吉布斯采样（Gibbs sampling），这是一种随机采样方法。

2.4.4.2 吉布斯采样

【知识卡片】

	1. 吉布斯采样：Gibbs sampling
	2. 吉布斯采样是一种随机采样方法。
	3. 吉布斯采样，用于在难以直接采样时，从某一多变量概率分布中近似抽取样本序列。
	4. 该序列可用于近似联合分布。
	5. Gibbs采样是一种迭代算法。
	6. Gibbs采样的核心是贝叶斯理论，围绕先验知识和观测数据，以观测值作为条件从而推断出后验分布。
	7. 吉布斯采样是一种马尔可夫链蒙特卡洛（MCMC）算法，可以看作是MetropolisHastings算法的一个特例。
	8. 吉布斯采样，每一步仅依赖于前一步的状态，，这是一个"马尔可夫链"。
	9. "马尔可夫链"在步数T 趋于无穷时，一定收敛（一定是一个平稳分布）。
	10. 吉布斯采样是马尔可夫链的一个特例。
	11. 马尔可夫链通常需很长时间才能趋于平稳分布，所以吉布斯采样算法的收敛速度较慢。

【原理】

  吉布斯采样算法的基本原理是通过随机采样，不断更新模型及其在各条输入序列中出现的位置，优化目标函数，当满足一定的迭代终止条件或者达到最大迭代次数时就得到了最终所求的模体。

【变量】

• 令$Q=\{Q_1,Q_2,...,Q_n\}$ 表示待查询变量
• $E=\{E_1,E_2,...,E_k\}$ 为证据变量
• 其取值为$e=\{e_1,e_2,...,e_k\}$
• 目标是计算后验概率$P(Q=q|E=e)$
• 其中$q=\{q_1,q_2,...,q_n\}$ 是待查询变量的一组取值

【例子】

• $Q=\{好瓜，甜度\}$
• $E=\{色泽，敲声，根蒂\}$
• $e=\{青绿，浊响，蜷缩\}$
• $P(Q=q|E=e)$
• $q=\{是，高\}$
• 【求这是好瓜且甜度高的概率？】

【过程】

1. 吉布斯采样算法先随机产生一个与证据$E=e$ 一致的样本$q^0$ 作为初始点；
2. 然后每步从当前样本出发产生下一个样本。
3. 算法先假设$q^t=q^{t-1}$；
4. 然后对非证据变量逐个进行采样改变其取值；
5. 怎么改变？根据贝叶斯网$B$ 和其他变量的当前取值(即$Z=z$) 计算获得;
6. 经过$T$ 次采样得到的于$q$ 一致的样本共有$n_q$ 个，则
   $$P(Q=q|E=e)\simeq \frac{n_q}{T}$$
7. T很大时，由马尔可夫链性质，吉布斯采样相当于根据$P(Q|E=e)$ 采样，从而保证了概率收敛于P(Q=q|E=e)

【算法】

3. 贝叶斯网梳理

3.1 贝叶斯网理解

	1. 贝叶斯网络是从条件概率的角度描述变量之间依赖关系的有向无环图（DAG）。
	2. 用G=(V,E) 来表示一个贝叶斯网络，其中V 表示变量，E 表示变量之间的条件概率，也作权重。
	3. 贝叶斯网揭示了变量之间的依赖关系，可以预测缺失值。
	4. 贝叶斯网络：Bayesian Network，简称BN
	5. 概率图模型（两大类）=贝叶斯网络+马尔可夫网络
	6. 特点：变量之间的因果关系

3.2 资料收集

• 简述贝叶斯网与其他概率图模型的区别

  贝叶斯网只是概率图模型的一种，它与其它概率图模型的特点之一就是，它描述变量之间的因果关系。如果给模型加上时间概念，则可以有马尔科夫链和高斯过程等。从空间上，如果随机变量是连续的，则有如高斯贝叶斯网络这样的模型。混合模型加上时间序列，则有隐马尔科夫模型、卡尔曼滤波、粒子滤波等模型。

• 马尔可夫链

马尔可夫链

3.3 贝叶斯网回顾

	1. 贝叶斯网，有向无环图
	2. 结点（参数独立性怎么解决），边（依赖，怎么构造，三种基本依赖），权值（参数的计算）
	3. 怎么构造B 的结构
	4. 查询，吉布斯采样-->马尔可夫链