哈夫曼树的构建

【哈夫曼树】当用 n 个结点（都做叶子结点且都有各自的权值）试图构建一棵树时，如果构建的这棵树的带权路径长度最小，称这棵树为“最优二叉树”，有时也叫“赫夫曼树”或者“哈夫曼树”。

【构建原则】权值大的节点离根近，权值小的节点离根远。

【预备知识】哈夫曼树是二叉树，只有0度节点和2度节点。

                      对于有n0个叶子节点的哈夫曼树，共有2*n0-1个节点。

【算法步骤】

1.初始化，ht数组的前n个weight成员变量赋值为权重，所有的双亲和左右儿子赋值为-1。

2.在前n个节点点构成的森林中选取权值最小的两个节点构成一棵新的二叉树代替原来的两个节点。

3.重复2直到森林中只剩一棵二叉树。

【案例】

输入：

7
5 2 9 11 8 3 7

输出：

请输入节点个数：7
请输入节点的权值：5 2 9 11 8 3 7
最小下标：1     次小下标：5
最小下标：0     次小下标：7
最小下标：6     次小下标：4
最小下标：2     次小下标：8
最小下标：3     次小下标：9
最小下标：10    次小下标：11
打印构建好的哈夫曼数组内容：
weiht  parent  lchild  rchild
5       8       -1      -1
2       7       -1      -1
9       10      -1      -1
11      11      -1      -1
8       9       -1      -1
3       7       -1      -1
7       9       -1      -1
5       8       1       5
10      10      0       7
15      11      6       4
19      12      2       8
26      12      3       9
45      -1      10      11

手动建树如下：

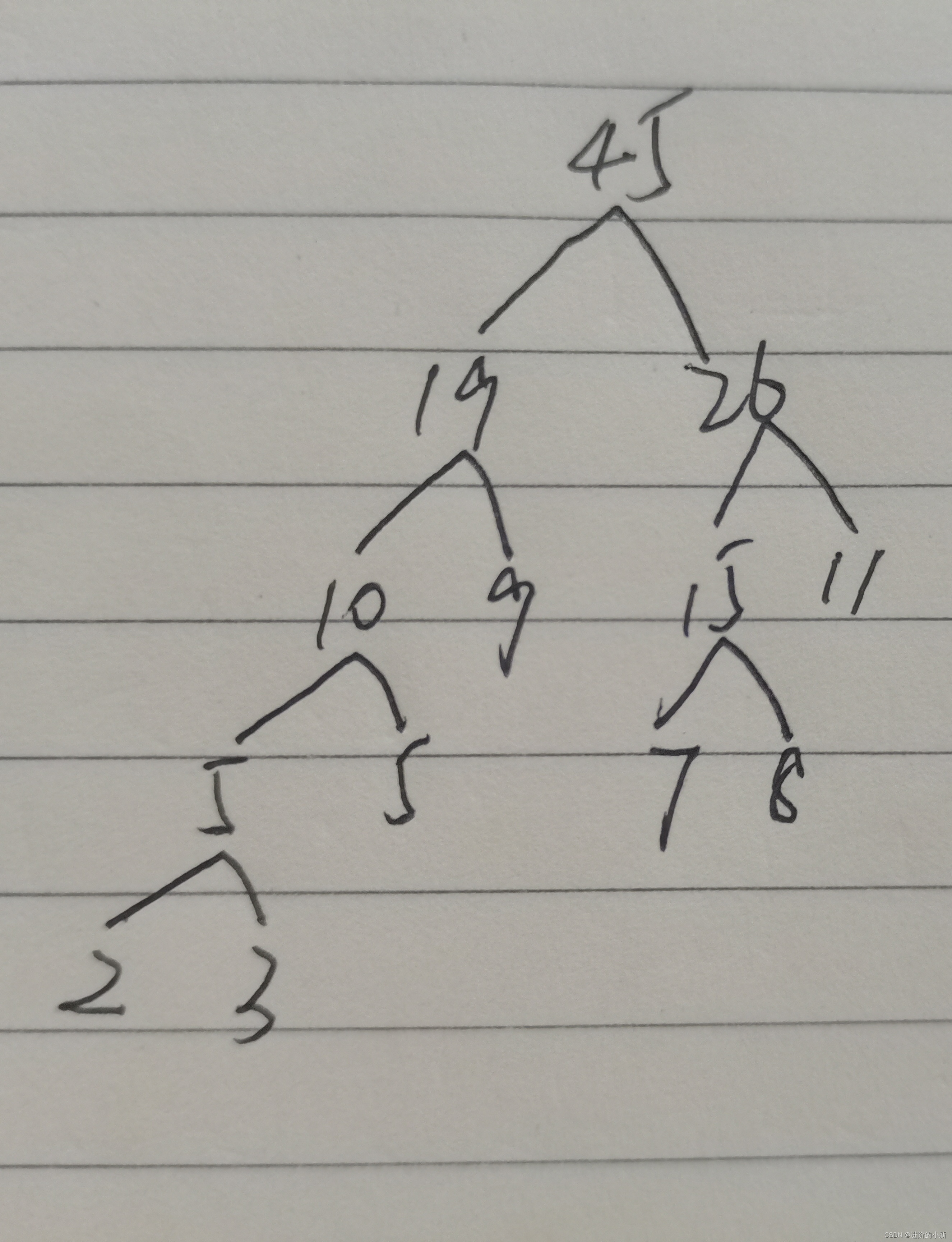
 注：代码严格按照左儿子的权值大于右儿子的权值执行，手动可能产生不同结果，但根节点的长度是一样的，最短带权路径长度也是一样的。

话不多说，上代码：

#include <stdio.h>

typedef struct node {
	int weight;
	int parent, lchild, rchild;
}HTNode;

void print(HTNode *ht, int n) {
	printf("打印构建好的哈夫曼数组内容：\n");
	printf("weiht  parent  lchild  rchild\n");
	for(int i=0;i<2*n-1;i++) 
		printf("%d\t%d\t%d\t%d\n",ht[i].weight,ht[i].parent,ht[i].lchild,ht[i].rchild);
}

void creatht(HTNode* ht, int n) {
	int min1, min2;
	int lnode, rnode;
	for(int i=n;i<2*n-1;i++) {
		min1 = min2 = 0x7fffffff;
		lnode = rnode = -1;
		for(int k=0;k<i;k++) { //在双亲还未被赋值的节点中找到权值最小的两个节点即对应下标
			if(ht[k].parent == -1) {
				if(ht[k].weight < min1) {
					min2 = min1, rnode = lnode;
					min1 = ht[k].weight, lnode = k;
				} else if(ht[k].weight < min2) {
					min2 = ht[k].weight, rnode = k;
				}
			}
		}
		printf("最小下标：%d\t",lnode);
		printf("次小下标：%d\n",rnode);
		ht[i].weight = ht[lnode].weight + ht[rnode].weight; //创建下标为i的新节点
		ht[i].lchild = lnode, ht[i].rchild = rnode;
		ht[lnode].parent = ht[rnode].parent = i; //左右儿子的双亲赋值为新节点 
	}
	print(ht, n);
}

int main() {
	int n;
	printf("请输入节点个数："); //初始化 
	scanf("%d",&n);
	printf("请输入节点的权值：");
	HTNode ht[2*n-1];
	for(int i=0;i<n;i++)
		scanf("%d",&ht[i].weight);
	for(int i=0;i<2*n-1;i++) 
		ht[i].parent = ht[i].lchild = ht[i].rchild = -1;
	creatht(ht, n);
	return 0;
}