当前位置:网站首页>[LOJ 6718] nine suns' weakened version (cyclic convolution, arbitrary modulus NTT)
[LOJ 6718] nine suns' weakened version (cyclic convolution, arbitrary modulus NTT)
2022-06-26 03:47:00 【DD(XYX)】
Topic
Given n , K n,K n,K , Satisfy K K K yes 2 2 2 The power of , seek
∑ K ∣ i , 0 ≤ i ≤ n ( n i ) \sum_{K|i,0\leq i\leq n} {n\choose i} K∣i,0≤i≤n∑(in)
Yes 998244 998244 998244 8 8 8 53 53 53 modulus .
1 ≤ n ≤ 1 0 15 , 1 ≤ K ≤ 2 15 1\leq n\leq10^{15},1\leq K\leq2^{15} 1≤n≤1015,1≤K≤215 .
Answer key
There seem to be few solutions to this problem on the Internet .
LOJ The unit root inversion method with very large constant is given in the discussion area , But just like 4 Lou said 
It is not difficult to find that the answer to this question is ( 1 + x ) n (1+x)^{n} (1+x)n Run length K K K The constant term of the cyclic convolution of . We directly cycle convolution to speed up the power of speed solution .
But the module is very grave , Don't do it NTT modulus , So we have to use Arbitrary modulus NTT / MTT( Universal convolution method to power of the five at that point is not good , can't make a good living ).
This time I finally Learned , no need __int128 了 ,
We get three congruence formulas :
{ x ≡ c 1 m o d m 1 x ≡ c 2 m o d m 2 x ≡ c 3 m o d m 3 \begin{cases} x\equiv c_1 &\mod m_1\\ x\equiv c_2 &\mod m_2\\ x\equiv c_3 &\mod m_3 \end{cases} ⎩⎪⎨⎪⎧x≡c1x≡c2x≡c3modm1modm2modm3
Let's merge the first two to get x ≡ k m o d m 1 m 2 x\equiv k\mod m_1m_2 x≡kmodm1m2 .
We make m 1 ′ m_1' m1′ by m 1 m_1 m1 modulus m 2 m_2 m2 Inverse element , m 2 ′ m_2' m2′ by m 2 m_2 m2 modulus m 1 m_1 m1 Inverse element ,
You can get : k = ( ( c 1 ⋅ m 2 ′ ) % m 1 ⋅ m 2 + ( c 2 ⋅ m 1 ′ ) % m 2 ⋅ m 1 ) % ( m 1 m 2 ) k=\left( (c_1\cdot m_2')\%m_1\cdot m_2 +(c_2\cdot m_1')\%m_2\cdot m_1\right)\%(m_1m_2) k=((c1⋅m2′)%m1⋅m2+(c2⋅m1′)%m2⋅m1)%(m1m2) ,
This process will not explode l o n g l o n g \rm long~long long long Of .
Then make x = t m 1 m 2 + k x=tm_1m_2+k x=tm1m2+k , that
t m 1 m 2 + k ≡ c 3 m o d m 3 ⇒ t ≡ ( c 3 − k ) ( m 1 m 2 ) − 1 m o d m 3 tm_1m_2+k\equiv c_3\mod m_3\\ \Rightarrow t\equiv(c_3-k)(m_1m_2)^{-1}\mod m_3 tm1m2+k≡c3modm3⇒t≡(c3−k)(m1m2)−1modm3
We want to know t m 1 m 2 m o d m 1 m 2 m 3 tm_1m_2\mod m_1m_2m_3 tm1m2modm1m2m3 Result , Just need to know t m o d m 3 t\mod m_3 tmodm3 Just the result of . Calculation t t t The process is not explosive l o n g l o n g \rm long~long long long Of , You don't need a turtle to ride .
At this time, we just need to guarantee the truth x < m 1 m 2 m 3 − m 1 m 2 x<m_1m_2m_3-m_1m_2 x<m1m2m3−m1m2 , Then calculate t m 1 m 2 + k tm_1m_2+k tm1m2+k What you get is real x x x Specify m o d \rm mod mod The result of taking the mold .
Time complexity O ( K log K log n ) O(K\log K\log n) O(KlogKlogn) .
CODE
#include<map>
#include<set>
#include<cmath>
#include<ctime>
#include<queue>
#include<stack>
#include<random>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<unordered_map>
#pragma GCC optimize(2)
using namespace std;
#define MAXN (1<<16|5)
#define LL long long
#define ULL unsigned long long
#define ENDL putchar('\n')
#define DB double
#define lowbit(x) (-(x) & (x))
#define FI first
#define SE second
#define PR pair<int,int>
#define UIN unsigned int
int xchar() {
static const int maxn = 1000000;
static char b[maxn];
static int pos = 0,len = 0;
if(pos == len) pos = 0,len = fread(b,1,maxn,stdin);
if(pos == len) return -1;
return b[pos ++];
}
// #define getchar() xchar()
LL read() {
LL f = 1,x = 0;int s = getchar();
while(s < '0' || s > '9') {
if(s<0)return -1;if(s=='-')f=-f;s = getchar();}
while(s >= '0' && s <= '9') {
x = (x<<1) + (x<<3) + (s^48);s = getchar();}
return f*x;
}
void putpos(LL x) {
if(!x)return ;putpos(x/10);putchar((x%10)^48);}
void putnum(LL x) {
if(!x) {
putchar('0');return ;}
if(x<0) putchar('-'),x = -x;
return putpos(x);
}
void AIput(LL x,int c) {
putnum(x);putchar(c);}
const int MOD = 998244853;
const int M1 = 1012924417,R1 = 5;
const int M2 = 1007681537,R2 = 3;
const int M3 = 1004535809,R3 = 3;
int n,m,s,o,k;
inline void MD(int &x) {
if(x>=MOD)x-=MOD;}
int qkpow(int a,LL b) {
int res = 1;
while(b > 0) {
if(b & 1) res = res *1ll* a % MOD;
a = a *1ll* a % MOD; b >>= 1;
}return res;
}
int qkpow(int a,int b,int MOD) {
int res = 1;
while(b > 0) {
if(b & 1) res = res *1ll* a % MOD;
a = a *1ll* a % MOD; b >>= 1;
}return res;
}
int om,xm[MAXN<<2];
int rev[MAXN<<2];
void NTT(int *s,int n,int op,int MOD,int R) {
for(int i = 1;i < n;i ++) {
rev[i] = (rev[i>>1]>>1) | ((i&1) ? (n>>1):0);
if(rev[i] < i) swap(s[i],s[rev[i]]);
}
om = qkpow(R,(MOD-1)/n,MOD); xm[0] = 1;
if(op < 0) om = qkpow(om,MOD-2,MOD);
for(int i = 1;i < n;i ++) xm[i] = xm[i-1] *1ll* om % MOD;
for(int k = 2,t = n>>1;k <= n;k <<= 1,t >>= 1) {
for(int j = 0;j < n;j += k) {
for(int i = j,l = 0;i < j+(k>>1);i ++,l += t) {
int A = s[i],B = s[i+(k>>1)];
s[i] = (A + xm[l]*1ll*B) % MOD;
s[i+(k>>1)] = (A +MOD- xm[l]*1ll*B%MOD) % MOD;
}
}
}
if(op < 0) {
int invn = qkpow(n,MOD-2,MOD);
for(int i = 0;i < n;i ++) s[i] = s[i]*1ll*invn % MOD;
}return ;
}
int a[MAXN<<1],b[MAXN<<1],c[MAXN<<1];
int a_[MAXN<<1],b_[MAXN<<1];
void polymul(int *A,int *B,int le) {
for(int i = 0;i < le;i ++) a_[i] = A[i],b_[i] = B[i];
NTT(A,le,1,M1,R1); NTT(B,le,1,M1,R1);
for(int i = 0;i < le;i ++) a[i] = A[i]*1ll*B[i] % M1;
for(int i = 0;i < le;i ++) A[i] = a_[i],B[i] = b_[i];
NTT(a,le,-1,M1,R1);
NTT(A,le,1,M2,R2); NTT(B,le,1,M2,R2);
for(int i = 0;i < le;i ++) b[i] = A[i]*1ll*B[i] % M2;
for(int i = 0;i < le;i ++) A[i] = a_[i],B[i] = b_[i];
NTT(b,le,-1,M2,R2);
NTT(A,le,1,M3,R3); NTT(B,le,1,M3,R3);
for(int i = 0;i < le;i ++) c[i] = A[i]*1ll*B[i] % M3;
for(int i = 0;i < le;i ++) A[i] = a_[i],B[i] = b_[i];
NTT(c,le,-1,M3,R3);
int v1 = qkpow(M2,M1-2,M1);
int v2 = qkpow(M1,M2-2,M2);
int v3 = qkpow(M1*1ll*M2%M3,M3-2,M3);
LL MD = M1*1ll*M2;
for(int i = 0;i < le;i ++) {
LL k = (v1*1ll*a[i]%M1*M2 + v2*1ll*b[i]%M2*M1) % MD;
int t = (c[i]+M3-k%M3) % M3 *1ll* v3 % M3;
A[i] = (MD % MOD * t % MOD + k) % MOD;
}
return ;
}
void polymuls(int *A,int le) {
for(int i = 0;i < le;i ++) a_[i] = A[i];
NTT(A,le,1,M1,R1);
for(int i = 0;i < le;i ++) a[i] = A[i]*1ll*A[i] % M1;
for(int i = 0;i < le;i ++) A[i] = a_[i];
NTT(a,le,-1,M1,R1);
NTT(A,le,1,M2,R2);
for(int i = 0;i < le;i ++) b[i] = A[i]*1ll*A[i] % M2;
for(int i = 0;i < le;i ++) A[i] = a_[i];
NTT(b,le,-1,M2,R2);
NTT(A,le,1,M3,R3);
for(int i = 0;i < le;i ++) c[i] = A[i]*1ll*A[i] % M3;
for(int i = 0;i < le;i ++) A[i] = a_[i];
NTT(c,le,-1,M3,R3);
int v1 = qkpow(M2,M1-2,M1);
int v2 = qkpow(M1,M2-2,M2);
int v3 = qkpow(M1*1ll*M2%M3,M3-2,M3);
LL MD = M1*1ll*M2;
for(int i = 0;i < le;i ++) {
LL k = (v1*1ll*a[i]%M1*M2 + v2*1ll*b[i]%M2*M1) % MD;
int t = (c[i]+M3-k%M3) % M3 *1ll* v3 % M3;
A[i] = (MD % MOD * t % MOD + k) % MOD;
}
return ;
}
int A[MAXN],B[MAXN],C[MAXN];
int main() {
LL N = read(); m = read();
if(m == 1) {
return AIput(qkpow(2,N),'\n'),0;
}
C[0] = 1; A[0] = 1; A[1] = 1;
while(N > 0) {
if(N & 1) {
polymul(C,A,m);
}
for(int i = 0;i < m;i ++) B[i] = A[i];
polymuls(A,m);
N >>= 1;
}
AIput(C[0],'\n');
return 0;
}
边栏推荐
- When the tiflash function is pushed down, it must be known that it will become a tiflash contributor in ten minutes
- The kotlin project is running normally and the R file cannot be found
- IEDA 突然找不到了compact middle packages
- Digital twin intelligent water service, breaking through the development dilemma of sponge City
- 2022.6.25 - leetcode. Un doigt d'épée. 091.
- Concept and implementation of QPS
- Redux thunk simple case, advantages, disadvantages and thinking
- Kotlin quick start
- Oracle技术分享 oracle 19.14升级19.15
- String到底能不能改变?
猜你喜欢

Request object, send request

Uni app QR code scanning and identification function

“再谈”协议
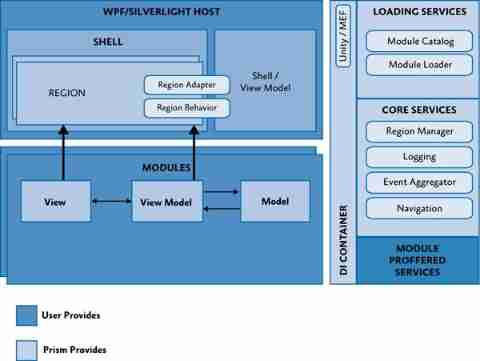
Prism framework

MapReduce执行原理记录

ABP framework Practice Series (III) - domain layer in depth
After Ali failed to start his job in the interview, he was roast by the interviewer in the circle of friends (plug)

Click event

Uni app custom selection date 2 (September 16, 2021)

Uni app custom drop-down selection list
随机推荐
Is Guoxin golden sun reliable? Is it safe to open a securities account?
Request object, send request
"Renegotiation" agreement
Introduction of mybatis invalid
redux-thunk 简单案例,优缺点和思考
Various errors in kitti2bag installation
169. most elements
You cannot call Glide. get() in registerComponents(), use the provided Glide instance instead
Kotlin uses viewpager2+fragment+bottomnavigationview to implement the style of the switching module of the bottom menu bar.
Slide the menu of uni app custom components left and right and click switch to select and display in the middle
MySQL高级部分( 四: 锁机制、SQL优化 )
Qixia fire department carries out fire safety training on construction site
816. 模糊坐标
js实现文字跑马灯效果
JS to achieve the effect of text marquee
Is it safe to open a fund account? How to apply
When the tiflash function is pushed down, it must be known that it will become a tiflash contributor in ten minutes
Binary search
Evaluation - analytic hierarchy process
[paper notes] supersizing self supervision: learning to grasp from 50K tries and 700 robot hours