当前位置:网站首页>WBC learning notes (II): practical application of WBC control
WBC learning notes (II): practical application of WBC control
2022-06-26 08:33:00 【Yu Getou】
This article mainly refers to the following articles , The purpose is to deepen my understanding of WBC Formula and understanding of multi priority task application .
Based on the null space method (NUB) Full body control of (WBC) Simple implementation of 
Control system input : The position of the slider on the track y h y_h yh, Position of each joint of the manipulator θ = [ θ 1 θ 2 θ 3 ] T \boldsymbol{\theta}=[\theta_1\ \theta_2\ \theta_3]^T θ=[θ1 θ2 θ3]T.
Control system output : The speed of each joint of the manipulator θ ˙ \boldsymbol{\dot{\theta}} θ˙.
Control the mission 1: Keep the end position of the manipulator at the point under the world coordinate system A = [ 2 0 ] T A=[2 \ 0]^T A=[2 0]T.
Control the mission 2: Make the end of the mechanical arm face x Axis .
1. Control scheme without priority
(1) Desired coordinates at the end
x d = [ 2 − y h 0 ] \boldsymbol{x}_{d}=\left[\begin{array}{c} 2 \\ -y_h \\ 0 \end{array}\right] xd=⎣⎡2−yh0⎦⎤
(2) Forward kinematics solution ( The end is relative to the origin )
x = [ x y θ ] = [ l 1 c 1 + l 2 c 12 + l 3 c 123 l 1 s 1 + l 2 s 12 + l 3 s 123 θ 1 + θ 2 + θ 3 ] \boldsymbol{x}=\left[\begin{array}{l} x \\ y \\ \theta \end{array}\right]=\left[\begin{array}{c} l_{1} c_{1}+l_{2} c_{12}+l_{3} c_{123} \\ l_{1} s_{1}+l_{2} s_{12}+l_{3} s_{123} \\ \theta_{1}+\theta_{2}+\theta_{3} \end{array}\right] x=⎣⎡xyθ⎦⎤=⎣⎡l1c1+l2c12+l3c123l1s1+l2s12+l3s123θ1+θ2+θ3⎦⎤
(3) Seeking inverse
take l 1 = l 2 = l 3 = 1 m l_1=l_2=l_3=1m l1=l2=l3=1m Plug in
x ˙ = J θ ˙ ↓ J = [ − s 1 − s 12 − s 123 − s 12 − s 123 − s 123 c 1 + c 12 + c 123 c 12 + c 123 c 123 1 1 1 ] ↓ θ ˙ = J † x ˙ \dot{\boldsymbol{x}}=J\boldsymbol{\dot{\theta}}\\ \downarrow\\ J=\left[\begin{array}{ccc} -s_{1}-s_{12}-s_{123} & -s_{12}-s_{123} & -s_{123} \\ c_{1}+c_{12}+c_{123} & c_{12}+c_{123} & c_{123} \\ 1 & 1 & 1 \end{array}\right]\\ \downarrow\\ \dot{\theta}=J^{\dagger} \dot{\boldsymbol{x}} x˙=Jθ˙↓J=⎣⎡−s1−s12−s123c1+c12+c1231−s12−s123c12+c1231−s123c1231⎦⎤↓θ˙=J†x˙
Properties of pseudo inverse : if J J J Inverse , be J † J^{\dagger} J† yes J J J The inverse of ; if J J J No inverse , be J † J^{\dagger} J† Satisfy θ ˙ = J † x ˙ \dot{\theta}=J^{\dagger} \dot{\boldsymbol{x}} θ˙=J†x˙ The least square solution of .
2. Control scheme with priority
For example, the position priority is higher than the direction priority
(1) Task breakdown
{ r 1 = [ x y ] T r 2 = θ ↓ { r 1 d = [ 2 − y h ] T r 2 d = 0 \left\{\begin{array}{l} \mathbf{r}_{1}=\left[\begin{array}{ll} x & y \end{array}\right]^{T} \\ \mathbf{r}_{2}=\theta \end{array}\right.\\ \downarrow\\ \left\{\begin{array}{l} \mathbf{r}_{1 d}=\left[\begin{array}{ll} 2 & -y_{h} \end{array}\right]^{T} \\ \mathbf{r}_{2 d}=0 \end{array}\right. { r1=[xy]Tr2=θ↓{ r1d=[2−yh]Tr2d=0
(2) Jacobian matrix solution
The specific parameter values of the matrix have been obtained above , Just break it down
{ J 1 = [ − s 1 − s 12 − s 123 − s 12 − s 123 − s 123 c 1 + c 12 + c 123 c 12 + c 123 c 123 ] J 2 = [ 1 1 1 ] \left\{\begin{array}{l} J_{1}=\left[\begin{array}{ccc} -s_{1}-s_{12}-s_{123} & -s_{12}-s_{123} & -s_{123} \\ c_{1}+c_{12}+c_{123} & c_{12}+c_{123} & c_{123} \end{array}\right] \\ J_{2}=\left[\begin{array}{lll} 1 & 1 & 1 \end{array}\right] \end{array}\right. ⎩⎨⎧J1=[−s1−s12−s123c1+c12+c123−s12−s123c12+c123−s123c123]J2=[111]
(3) Plug in WBC The formula
θ ˙ = J 1 † r ˙ 1 + ( I − J 1 † J 1 ) J 2 † r ˙ 2 \dot{\theta}=J_{1}^{\dagger} \dot{\mathbf{r}}_{1}+\left(I-J_{1}^{\dagger} J_{1}\right) J_{2}^{\dagger} \dot{\mathbf{r}}_{2} θ˙=J1†r˙1+(I−J1†J1)J2†r˙2
In actual control , Input the obtained velocity value into the controller of the joint ( Such as PID controller ) Control the joint motor
边栏推荐
- Intra class data member initialization of static const and static constexpr
- 你为什么会浮躁
- 2020-10-17
- Apple motherboard decoding chip, lightning Apple motherboard decoding I.C
- Compiling owncloud client on win10
- Design of reverse five times voltage amplifier circuit
- Recognize the interruption of 80s51
- xxl-job配置告警邮件通知
- 监听iPad键盘显示和隐藏事件
- Recyclerview item gets the current position according to the X and Y coordinates
猜你喜欢

Method of measuring ripple of switching power supply
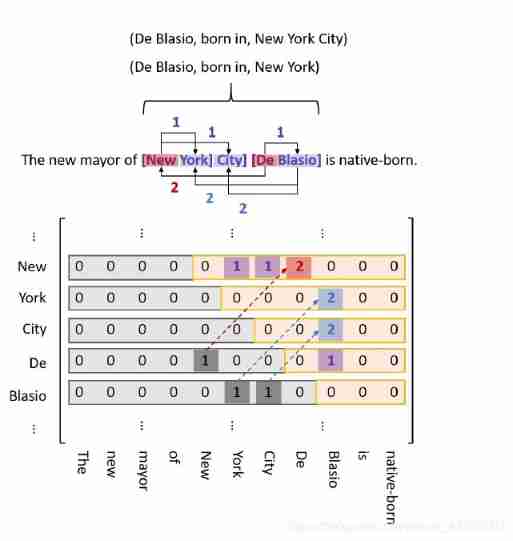
Relationship extraction --tplinker

The difference between push-pull circuit drive and totem pole drive

Transformers loading Roberta to implement sequence annotation task

加密的JS代码,变量名能破解还原吗?

What are the conditions for Mitsubishi PLC to realize Ethernet wireless communication?

Comparison between Apple Wireless charging scheme and 5W wireless charging scheme

Learning signal integrity from scratch (SIPI) -- 3 challenges faced by Si and Si based design methods

Relationship extraction --r-bert

(vs2019 MFC connects to MySQL) make a simple login interface (detailed)
随机推荐
JS file message invalid character error
Comparison between Apple Wireless charging scheme and 5W wireless charging scheme
STM32 project design: smart home system design based on stm32
STM32 encountered problems using encoder module (library function version)
SOC wireless charging scheme
STM32 project design: an e-reader making tutorial based on stm32f4
Diode voltage doubling circuit
在同花顺开户证券安全吗,
STM32 based d18s20 (one wire)
leetcode2022年度刷题分类型总结(十二)并查集
[postgraduate entrance examination] group planning exercises: memory
FFmpeg音视频播放器实现
Compiling owncloud client on win10
Whale conference provides digital upgrade scheme for the event site
Learning signal integrity from scratch (SIPI) -- 3 challenges faced by Si and Si based design methods
Batch execute SQL file
Relationship extraction -- casrel
2020-10-20
(1) Turn on the LED
(5) Matrix key