300. longest increasing subsequence ●●

300. The longest increasing subsequence ●●

describe

Give you an array of integers nums , Find one of them The length of the longest strictly increasing subsequence .

Subsequence Is a sequence derived from an array , Delete （ Or do not delete ） Elements in an array without changing the order of the rest . for example ,[3,6,2,7] It's an array [0,3,1,6,2,2,7] The subsequence .

Example

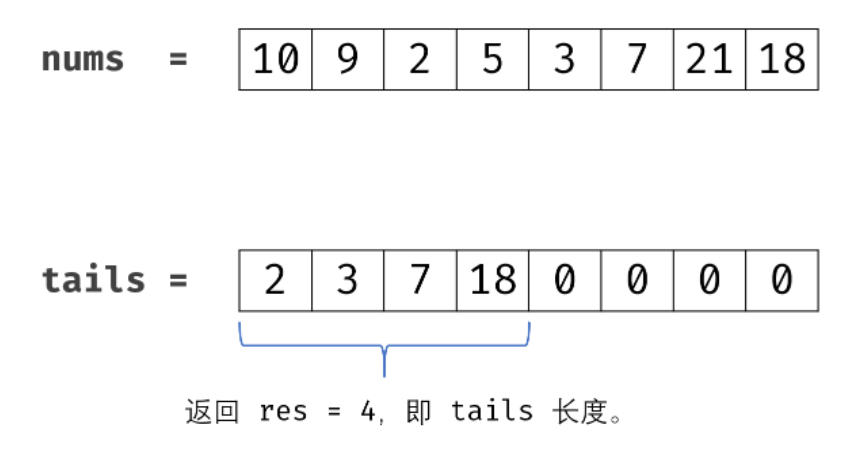
Input ：nums = [10,9,2,5,3,7,101,18]
Output ：4
explain ： The longest increasing subsequence is [2,3,7,101], So the length is 4 .

Answer key

1. Dynamic programming

1. dp[i] Says to the first i A digital nums[i] Increment the sequence length for the longest ending ;
2. if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
   Location i The longest ascending subsequence of is equal to j from 0 To i-1 The longest ascending subsequence at each position + 1 The maximum of .
   Note that this is not to dp[i] And dp[j] + 1 Compare , But we need take dp[j] + 1 The maximum of .
3. every last i, Corresponding dp[i]（ That is, the longest ascending subsequence ） Starting size is at least 1;
4. Double loop , Traversing from front to back .

• Time complexity ：$O(n^2)$, among n Is an array nums The length of . The number of states of dynamic programming is n, Calculation state dp[i] when , need O(n) Time traversal dp[0…i−1] All states .
• Spatial complexity ：O(n), Additional length required is n Of dp Array .

class Solution {
    
public:
    int lengthOfLIS(vector<int>& nums) {
    
        int n = nums.size();
        int ans = 1;
        vector<int> dp(n, 1);   	// dp[i]  Says to the first i The longest increment sequence length ending with a number 
        for(int i = 1; i < n; ++i){
    	// nums[i] ending 
            for(int j = 0; j < i; ++j){
    
                if(nums[i] > nums[j]){
    
                    dp[i] = max(dp[i], dp[j] + 1);	//  Ascending time ,0 To i-1 The longest ascending subsequence at each position  + 1
                }
            }  
            ans = max(ans, dp[i]);	//  Taking the maximum 
        }
        return ans;
    }
};

2. DP + Two points search

By redesigning State definition , Make the whole dp For one Sort list ; In this way, every dp[k] when , You can go through Dichotomy Traverse [0,k) Interval elements , Change the complexity of this part from O(N) Down to O(logN).

Definition dp[i] Express The longest increment sequence length is i+1 Minimum ending number of , Such as {1, 2, 4, 3} in , The longest increment sequence length is 3 Minimum ending number of dp[2] = 3;

here dp Arrays must be strictly incremented , namely k < n From time to tome dp[ k ] < dp[ n ], When the value of the tail element of each subsequence is minimized as much as possible , The longer the subsequence , The element value at the end of the sequence must be larger .（ It can be proved to the contrary ）.

The steps are ：

1. newly build dp Array , It is used to store the longest incremental sequence with a length of i+1 Minimum ending number of , initialization dp[0] = nums[0];
2. Traversal array nums, Compare and insert each element ,
   1） If dp All the elements in the are smaller than it , Then a new element is inserted at the end ;
   2） otherwise , Find the first greater than or equal to by dichotomy nums[i] The location of , Replace .

All in all , Thought is to let dp[i] The storage sequence length is i+1 Of Minimum trailing number . such ,dp It may not be the real longest ascending subsequence , But its length is the final subsequence length . such as {1, 2, 9, 10, 3, 4, 5} The replacement process of .

• Time complexity $O(NlogN)$ ： Traverse nums List needs O(N), At every nums[i] Dichotomy requires O(logN).
• Spatial complexity O(N) ： tails The list takes up extra space of linear size .

class Solution {
    
public:
    int lengthOfLIS(vector<int>& nums) {
    
        vector<int> dp;                 // dp[i]  Indicates that the longest increment sequence length is i+1 Minimum ending number of 
        dp.emplace_back(nums[0]);		// dp initialization 
        for(int i = 1; i < n; ++i){
    
            int l = 0;
            int r = dp.size()-1;
            if(dp[r] < nums[i]){
            // dp The maximum number of arrays is less than nums[i], Tail-insert element 
                dp.emplace_back(nums[i]);
                continue;
            }                           // nums[i] stay dp Array range 
            while(l <= r){
                  //  Binary search for the first greater than or equal to nums[i] The location of , Replace 
                int m = l + (r-l) / 2;
                if(dp[m] >= nums[i]){
       //  If it is not required to increase strictly , Take this trip >= Change it to >, That's ok 10 Of < Change it to <=
                    r = m - 1;
                }else{
    
                    l = m + 1;
                }
            }
            dp[l] = nums[i];            //  Element substitution 
        }
        return dp.size();
    }
};