当前位置:网站首页>Basics of Probability Theory - 13 - Poisson Distribution (Poisson Distribution)
Basics of Probability Theory - 13 - Poisson Distribution (Poisson Distribution)
2022-08-05 14:33:00 【why why】
This paper records the Poisson distribution.
泊松分布
- 假设已知events in unit time (或者单位面积) 内发生的平均次数为 \lambda, Then the Poisson distribution describes:events in unit time (或者单位面积) The specific number of occurrences within is k 的概率.
- 概率质量函数: p(X=k | \lambda)=\frac{e^{-\lambda} \lambda^{k}}{k !} .
- 期望: \mathbb{E}[X]=\lambda
- 方差: \operatorname{Var}[X]=\lambda
The source of the Poisson distribution
- The number of occurrences per unit time of the Poisson distribution is X,平均次数为\lambda
- Let the observed time period be [0,1),Take a large natural numbern,put the time period[0,1)divided into equal lengthsn段:
- We make the following two assumptions:
- 在每段 l_{i} 内, The probability of exactly one accident,Approximate the length of this time \frac{1}{n} 成正比,可设为 \frac{\lambda}{n} .当n很大时, \frac{1}{n} 很小时,在 l_{i} in such a short period of time,It is impossible to have two or more accidents.因此在 l_{i} The probability of no accident during this time period is 1-\frac{\lambda}{n} .
- l_{i}, \ldots, l_{n} Whether an accident occurs in each segment is independent 把在 [0,1) The number of accidents that occurred during the time period Xregarded as innA small period after the division l_{i}, \ldots, l_{n} The number of time periods in which the accident occurred,According to the above two assumptions, X should be served 从二项分布 B\left(n, \frac{\lambda}{n}\right) .于是,我们有
- 注意到当 n \rightarrow \infty 取极限时,我们有
- 因此
从上述推导可以看出:The Poisson distribution can be obtained as the limit of the binomial distribution.一般的说,若 X \sim B(n, p) ,其中n很大, p很小,因而 n p=\lambda 不太大时, XThe distribution is close to the Poisson distribution P(\lambda) .This fact can sometimes convert the more difficult binomial distribution into a Poisson distribution to calculate.
Python 实现
scipyThe package supports modeling Poisson distributions
查表
Check the cumulative probability.查询 \lambda =100,The number of occurrences is less than or equal to120的概率:
from scipy import stats
p = stats.poisson.cdf(120, 100)
print(p)
>>>
0.9773306709216473随机数生成
生成服从
=50的泊松分布随机数100个:
from scipy import stats
# 设置random_state时,The random number generated each time is the same.不设置或为None时,The random numbers generated multiple times are different
sample = stats.poisson.rvs(mu=50, size=100, random_state=3)
print(sample)
>>>
[51 45 60 40 34 53 54 45 45 49 51 46 48 61 47 53 47 48 45 49 52 45 43 50
50 54 54 47 47 46 36 72 54 55 52 37 42 41 54 54 55 58 53 53 51 43 58 38
63 50 44 53 48 43 53 45 67 37 51 42 54 47 59 55 54 55 55 46 60 43 54 45
59 44 58 45 51 58 56 47 54 33 55 50 58 49 60 37 51 43 50 52 52 45 42 44
49 54 52 48]
参考资料
边栏推荐
- The actual use of EOSJS in China Mobile Chain
- 获取淘宝/天猫购买到商品的订单详情——buyer_order_detail
- 自媒体人必看的9个网站,每一个都很实用,值得收藏
- The operation process of uploading pictures to Taobao - upload_img
- LeetCode Question of the Day (1706. Where Will the Ball Fall)
- Oracle数据迁移实用入门
- 高效会议纪要重点
- 中金财富炒股怎样线上开户?有没有安全上的问题??
- Do wealth management products only see the principal but not the income?
- ‘proxy‘ config is set properly,see“npm help config“
猜你喜欢

OneNote 教程,如何在 OneNote 中插入表格并设置其格式?

day14·私有化属性

ES6解构详解

C#员工考勤管理系统源码 考勤工资管理系统源码

An in-depth long article discusses the simplification and speedup of JOIN operations
自媒体人必看的9个网站,每一个都很实用,值得收藏

Use Redis source code to compile and release Redis For Windows distribution package for Windows

顺序表(上)
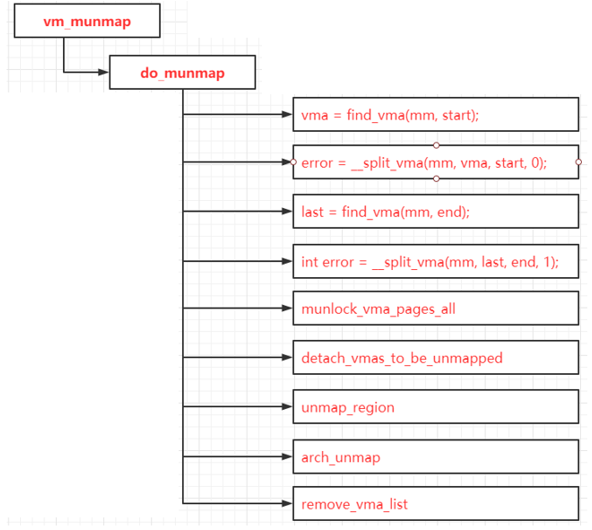
mmap kernel implementation and physical memory organization

NFT卡牌游戏系统Dapp开发(NFT链游)
随机推荐
2022最新综述 | 面向大规模场景的小目标检测:综述和 benchmark
C#员工考勤管理系统源码 考勤工资管理系统源码
神经网络的原理和应用,神经网络理论及应用
HDD Hangzhou Station • ArkUI makes development more flexible
获取淘宝/天猫购买到商品的订单详情——buyer_order_detail
内存问题难定位,那是因为你没用ASAN
day8·函数封装
目前民生期货这家期货公司怎么样?安全吗?
map 和 forEach 的区别
-ST表模板
JSCH 简单使用
Steps to update data to database and cache
使用 Redis 源码编译发布 Windows 版 Redis For Windows 发行包
[CUDA study notes] What is GPU computing
shell实现加密压缩文件自动解压
20款短视频自媒体必备工具,让你的运营效率翻倍
'proxy' config is set properly, see "npm help config"
抖音自媒体账号被限流?这3种方法教你如何鉴别
ES6解构详解
cookie、session、tooken