Visual explanation of clockwise inner curve in Green's formula hole digging method

Video Explanation ： An intuitive explanation of the clockwise inner curve in Green's formula hole digging method
When using Green's formula , Take the curve counterclockwise as the positive direction , But if there are singularities in the region surrounded by the curve , Green's formula cannot be used directly , You need to use the hole digging method first , The inner curve is clockwise , The mantra that people remember is usually “ External inversion and internal smoothness ”, As shown in the figure ,A Is the singular point on the plane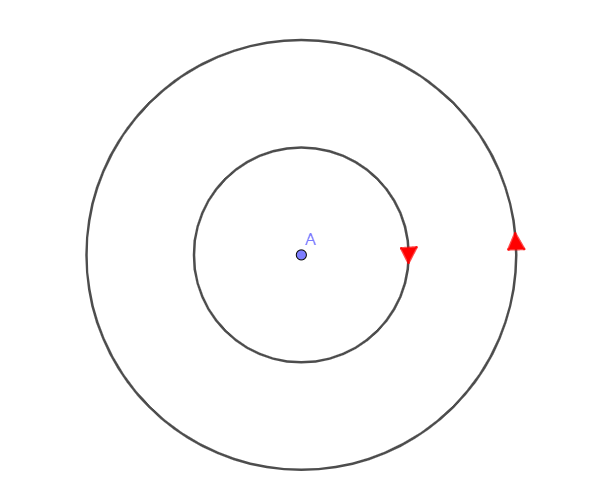
Of course, the curve may not be as smooth as the diagram , It may be uneven , Such as this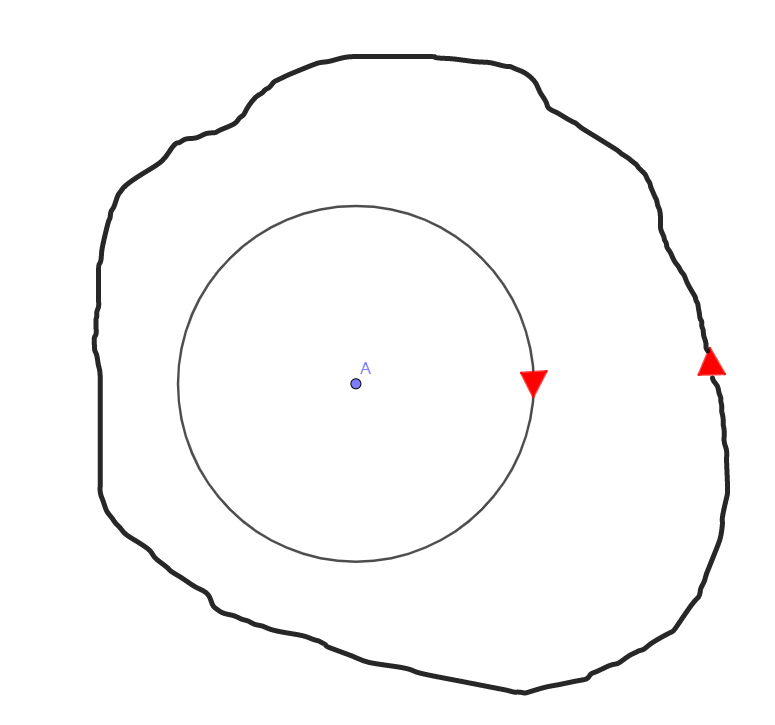

To make the drawing simple , This article will use simpler surfaces

So why is the inner curve clockwise , This article gives you an intuitive explanation .

Let's start with a surface like this , The enclosed area is yellow , As shown in the figure

This region does not contain singularities , So you can safely use Green's formula
$${\oint }_C={\int }_{C1}+{\int }_{l1}+{\int }_{C2}+{\int }_{l2}={\iint }_D$$

We're going to make a point B and C, spot D and E Gradually approach , Until it coincides , As shown in the figure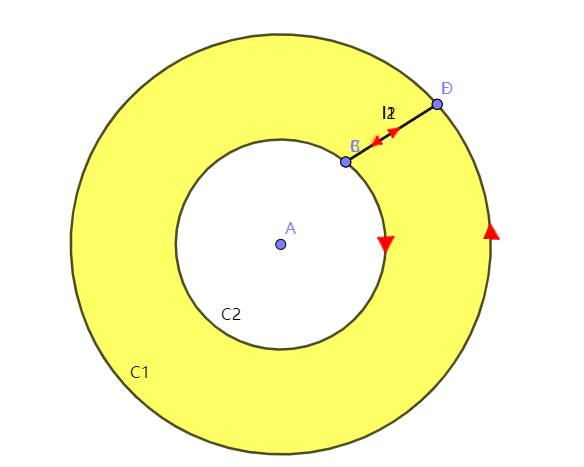

here $l1$ and $l2$ coincidence , In the opposite direction , be
$${\int }_{l1}+{\int }_{l2}=0$$
therefore
$${\oint }_C={\int }_{C1}+{\int }_{l1}+{\int }_{C2}+{\int }_{l2}={\int }_{C1}+{\int }_{C2}={\iint }_D$$
So we can put $l1$ and $l2$ Get rid of

So in the end, we can get
$${\oint }_{C1+C2}={\iint }_D$$