当前位置:网站首页>1259. 不相交的握手 动态规划
1259. 不相交的握手 动态规划
2022-07-23 16:33:00 【钰娘娘】
1259. 不相交的握手
偶数 个人站成一个圆,总人数为
num_people。每个人与除自己外的一个人握手,所以总共会有num_people / 2次握手。将握手的人之间连线,请你返回连线不会相交的握手方案数。
由于结果可能会很大,请你返回答案 模
10^9+7后的结果。示例 1:
输入:num_people = 2 输出:1示例 2:
输入:num_people = 4 输出:2 解释:总共有两种方案,第一种方案是 [(1,2),(3,4)] ,第二种方案是 [(2,3),(4,1)] 。示例 3:
输入:num_people = 6 输出:5示例 4:
输入:num_people = 8 输出:14提示:
2 <= num_people <= 1000num_people % 2 == 0
做题结果
成功,这题大概属于困难题中特别简单的
方法:动态规划
- 假设有 x 个人,我们从中任选了一个人 a,这个 a和一个人握手,要保证后续有解,则分割出的两部分必须都为偶数
- a 握手以后,还剩下,x-2个人没握手,x 握手以后,把剩余人员通过握手的连线分割为两部分,假设其中一个部分为 y 个人,则剩余部分为 x-2-y 个人
- 这个 y 人握手问题,就化解为了 x 人握手的子问题,枚举 所有可行的 y 和 x-2-y 握手可能性,两者互不干涉,可相乘处理
优化
- 由于都是偶数,我们只关心有多少对握手,可将空间范围缩减为 n/2
- 一边分割为 y 人,一边分割为 x-2-y 人,与反过来的结果是相同的,那么对于两边数目不同的情况,可以乘以2,从而减少一半循环次数,特别注意的是,当 y=x-2-y时,只有一种可能性,
class Solution {
public int numberOfWays(int numPeople) {
int half = numPeople/2;
long[] dp = new long[half+1];
long MOD = (long) (1e9+7);
dp[0]=1;
for(int i = 1; i <= half; i++){
for(int j = 0; j < i-j-1; j++){
dp[i]+=dp[j]*dp[i-j-1]*2;
dp[i] = dp[i]%MOD;
}
if(i%2!=0){
dp[i]+=dp[i/2]*dp[i-i/2-1];
dp[i] = dp[i]%MOD;
}
}
return (int) dp[half];
}
}时间复杂度:O(n)
空间复杂度:O(n)
边栏推荐
猜你喜欢

How to realize the digital transformation of the banking industry

入门学习3D建模一般会遇到哪些问题?实在是太多了
错误“ Failed to fetch “xxx”Temporary failure resolvingW: Some index files failed to download“解决办法

Deep learning learning record - update of learning rate of optimizer

Three things programmers want to do most | comics

【2020】【论文笔记】基于Rydberg原子的——
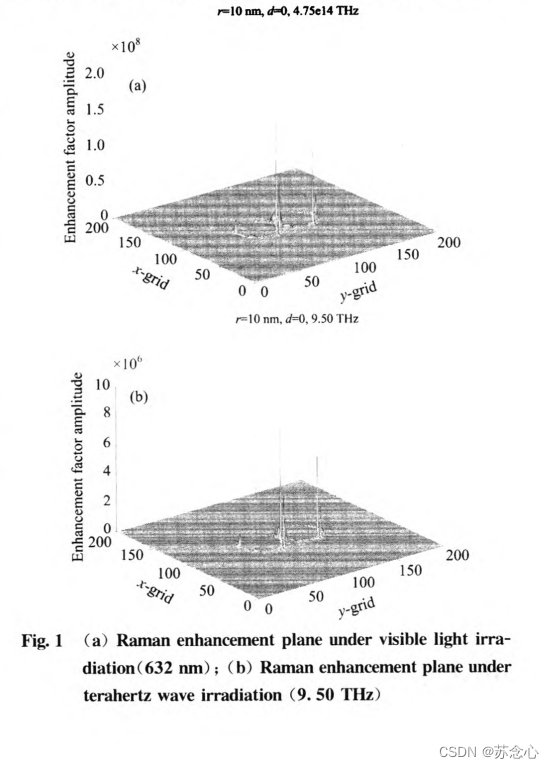
【2013】【论文笔记】太赫兹波段纳米颗粒表面增强拉曼——

Rhcsa notes 3
![[jzoof] 13 plage de mouvement du robot](/img/c3/56ae78f19578ff8ad8d9b824b7d99f.png)
[jzoof] 13 plage de mouvement du robot
![[whole process of game modeling model production] 3ds Max and ZBrush produce radio receivers](/img/c9/302a52d2c9f6fc3b5971e9a0ea55e6.png)
[whole process of game modeling model production] 3ds Max and ZBrush produce radio receivers
随机推荐
Where should we start to learn modeling from zero foundation? How to learn game modeling well?
Common problems of sklearn classifier
Have a safe summer vacation, no holidays! Please keep these summer safety tips
【JZOF】13機器人的運動範圍
UAV circumnavigating an unknown target under a GPS-deniedenvironment with range-only measurements翻译
Awk from introduction to earth (16) comprehensive case of awk
Huawei fat thin AP switching method
【2018】【论文笔记】石墨烯场效应管及【2】——石墨烯的制备、转移
DDD: how to use domain driven design to avoid writing journal code
接口测试概述
The great heat of the twenty-four solar terms
How to become a modeler? Which is more popular, industrial modeling or game modeling?
integer 和==比较
自学3D建模能不能成功?自学能就业吗?
大佬在线复盘:我在训练 DALL·E 时犯过的错
How does the NiO mechanism of jetty server cause out of heap memory overflow
SQLZOO——SELECT from Nobel Tutorial
怎么将word中的times new roman的双引号替换成宋体双引号
Is it suitable for learning 3D modeling? You can't lose one of these five points
Jetty 服务器的 NIO 机制是如何导致堆外内存溢出的

