牛客编程题--必刷101之动态规划(一文彻底了解动态规划)

补充知识

基础概念：动态规划（Dynamic Programming，DP）是运筹学的一个分支，是求解决策过程最优化的过程。

目的：动态规划问题的⼀般形式就是求最值。

解题思想：
1、将大问题进行拆分
2、以这个最小的结构为基础向上推导，进而得到一种不同层级解之间的关系 。这有点像数学归纳法。就是把你拆分的一步步之间的关系使用数学的推导公式来表示出来，这个公式用递归是很容易实现的。
3、考虑边界：要使用到递归，那么就不得不考虑边界问题了。

动态规划三要素：

• 最优子结构，上文提到的拆分到的最小的那一步。
• 边界 ，涉及到递归必须考虑的问题。
• 状态转移方程 ，拆分过程中不同步之间的关系。【重点】

思维框架：明确「状态」 -> 定义 dp 数组/函数的含义 -> 明确「选择」-> 明确 base
case。

基本思想：将待求解的问题分解成若干个相互联系的子问题，先求解子问题，然后从这些子问题的解得到原问题的解；对于重复出现的子问题，只在第一次遇到的时候对它进行求解，并把答案保存起来，让以后再次遇到时直接引用答案，不必重新求解。动态规划算法将问题的解决方案视为一系列决策的结果

1、斐波那契数列

直接递归方法即可

public class Solution {
    
    public int Fibonacci(int n) {
    
        if(n <=2){
    
            return 1;
        }else
            return Fibonacci(n-1)+ Fibonacci(n-2); 
    }
}

写代码虽然简洁易懂，但是⼗分低效，低效在哪⾥？假设 n = 20，请画出递归树。

这个递归树怎么理解？就是说想要计算原问题 f(20) ，我就得先计算出⼦问题 f(19) 和 f(18) ，然后要计算 f(19) ，我就要先算出⼦问题 f(18)和 f(17) ，以此类推。最后遇到 f(1) 或者 f(2) 的时候，结果已知，就能直接返回结果，递归树不再向下⽣⻓了。

算法的时间复杂度： 子问题个数 * （单个子问题时间）= O(2^n)
这个算法的时间复杂度为 ，指数级别，爆炸。

算法低效的原因：存在⼤量重复计算，⽐如f(18) 被计算了两次，⽽且你可以看到，以 f(18) 为根的这个递归树体量巨⼤，多算⼀遍，会耗费巨⼤的时间。

动态规划问题性质：重叠⼦问题

优化过程1（数组）

思想：其实思想也很简单，将每一轮计算的结果保存到数组中，然后再返回结果，每次遇到一个子问题先在数组中查找一下，如果已经计算，直接进行使用即可。

int fib(int N) {
    
	if (N < 1) return 0;
	// 数组全初始化为 0
	vector<int> memo(N + 1, 0);
	// 初始化最简情况
	return helper(memo, N);
}
int helper(vector<int>& memo, int n) {
    
	// base case
	if (n == 1 || n == 2) return 1;
	// 已经计算过
	if (memo[n] != 0) return memo[n];
		memo[n] = helper(memo, n - 1) + helper(memo, n - 2);
	return memo[n];
}

将把⼀棵存在巨量冗余的递归树通过「剪枝」，改造成了⼀幅不存在冗余的递归图，极⼤减少了⼦问题（即递归图中节点）的个数。

本算法的时间复杂度是 O(n)
这种解法和迭代的动态规划已经差不多了，只不过这种⽅法叫做「⾃顶向下」，动态规划叫做「⾃底向上」

啥叫「⾃顶向下」？
是从上向下延伸，都是从⼀个规模较⼤的原问题⽐如说 f(20) ，向下逐渐分解规模，直
到 f(1) 和 f(2) 触底，然后逐层返回答案，这就叫「⾃顶向下」。

啥叫「⾃底向上」？
反过来，我们直接从最底下，最简单，问题规模最⼩的 f(1) 和 f(2) 开始往上推，直到推到我们想要的答案 f(20)，这就是动态规划的思路，这也是为什么动态规划⼀般都脱离了递归，⽽是由循环迭代 完成计算。

优化过程2（dp表）

其实思路跟优化过程1是一样的，从这张表进行自底向上

int fib(int N) {
    
	vector<int> dp(N + 1, 0);
	// base case
	dp[1] = dp[2] = 1;
	for (int i = 3; i <= N; i++)
		dp[i] = dp[i - 1] + dp[i - 2];
	return dp[N];
}

优化过程3

根据斐波那契数列的状态转移⽅程，当前状态只和之前的两个状态有关，其实并不需要那么⻓
的⼀个 DP table 来存储所有的状态，只要想办法存储之前的两个状态就⾏了。所以，可以进⼀步优化，把空间复杂度降为 O(1)：

int fib(int n) {
    
	if (n == 2 || n == 1)
		return 1;
	int prev = 1, curr = 1;
	for (int i = 3; i <= n; i++) {
    
		int sum = prev + curr;
		prev = curr;
		curr = sum;
	}
	return curr;
}

2、凑零钱问题

题目描述：给你 k 种⾯值的硬币，⾯值分别为 c1, c2 … ck ，每种硬币的数量⽆限，再给⼀个总⾦额 amount ，问你最少需要⼏枚硬币凑出这个⾦额，如果不可能凑出，算法返回 -1

⽐如说 k = 3 ，⾯值分别为 1，2，5，总⾦额 amount = 11 。那么最少需要 3 枚硬币凑出，即 11 = 5 + 5 + 1。

暴力递归：

1、找到最优子结构

补充内容：要符合「最优⼦结构」，⼦问题间必须互相独⽴
举例说明：原问题是考出最⾼的总成绩，那么你的⼦问题就是要把语⽂考到最⾼，数学考到最⾼……
为了每门课考到最⾼，你要把每门课相应的选择题分数拿到最⾼，填空题分数拿到最⾼…… 当然，最终就是你每门课都是满分，这就是最⾼的总成绩。
得到了正确的结果：最⾼的总成绩就是总分。因为这个过程符合最优⼦结构，“每门科⽬考到最⾼”这些⼦问题是互相独⽴，互不⼲扰的。

当前问题：回到凑零钱问题，为什么说它符合最优⼦结构呢？⽐如你想求 amount =11 时的最少硬币数（原问题），如果你知道凑出 amount = 10 的最少硬币数（⼦问题），你只需要把⼦问题的答案加⼀（再选⼀枚⾯值为 1 的硬币）就是原问题的答案，因为硬币的数量是没有限制的，⼦问题之间没有相互制约，是互相独⽴的。

2、如何列出正确的状态转移⽅程？

• 先确定「状态」，也就是原问题和⼦问题中变化的变量。由于硬币数量⽆限，所以唯⼀的状态就是⽬标⾦额 amount 。
• 然后确定 dp 函数的定义：当前的⽬标⾦额是 n ，⾄少需要 dp(n) 个硬币凑出该⾦额。
• 然后确定「选择」并择优，也就是对于每个状态，可以做出什么选择改变当前状态。

当前问题：⽆论当的⽬标⾦额是多少，选择就是从⾯额列表coins 中选择⼀个硬币，然后⽬标⾦额就会减少：

# 伪码框架
def coinChange(coins: List[int], amount: int):
	# 定义：要凑出⾦额 n，⾄少要 dp(n) 个硬币
	def dp(n):
	# 做选择，选择需要硬币最少的那个结果
		for coin in coins:
			res = min(res, 1 + dp(n - coin))
		return res
	# 我们要求的问题是 dp(amount)
	return dp(amount)

• 最后明确 base case，显然⽬标⾦额为 0 时，所需硬币数量为 0；当⽬标⾦额 ⼩于 0 时，⽆解，返回 -1：

def coinChange(coins: List[int], amount: int):
	def dp(n):
		# base case
		if n == 0: return 0
		if n < 0: return -1
		# 求最⼩值，所以初始化为正⽆穷
		res = float('INF')
		for coin in coins:
			subproblem = dp(n - coin)
			# ⼦问题⽆解，跳过
			if subproblem == -1: continue
			res = min(res, 1 + subproblem)
		return res if res != float('INF') else -1
	return dp(amount)

状态转移⽅程其实已经完成了，以上算法已经是暴⼒解法了，以上代码的数学形式就是状态转移⽅程：
$$dp(n)=\{\begin{array}{l}0,n=0\\ -1,n<0\\ \min \{dp(n-\mathrm{coin})+1\mid \mathrm{coin}\in \text{ coins }\},n>0\end{array}$$

继续优化：消除重叠子问题【⽐如amount = 11, coins = {1,2,5} 时画出递归树看看：】

使用数组消除重叠子问题

def coinChange(coins: List[int], amount: int):
	memo = dict()
	def dp(n):
		# 查字典，避免重复计算
		if n in memo: return memo[n]
		if n == 0: return 0
		if n < 0: return -1
		res = float('INF')
		for coin in coins:
			subproblem = dp(n - coin)
			if subproblem == -1: continue
			res = min(res, 1 + subproblem)
		# 记⼊字典中
		memo[n] = res if res != float('INF') else -1
		return memo[n]
	return dp(amount)

使用dp表来消除重叠子问题

dp[i] = x 表⽰，当⽬标⾦额为 i 时，⾄少需要 x 枚硬币。
int coinChange(vector<int>& coins, int amount) {
    
	// 数组⼤⼩为 amount + 1，初始值也为 amount + 1
	vector<int> dp(amount + 1, amount + 1);
	// base case
	dp[0] = 0;
	for (int i = 0; i < dp.size(); i++) {
    
		// 内层 for 在求所有⼦问题 + 1 的最⼩值
		for (int coin : coins) {
    
			// ⼦问题⽆解，跳过
			if (i - coin < 0) continue;
			dp[i] = min(dp[i], 1 + dp[i - coin]);
		}
	}
	return (dp[amount] == amount + 1) ? -1 : dp[amount];
	}

具体题目：

兑换零钱(一)

题目描述：

• 给定数组arr, arr中所有的值都为正整数环重复
• arr中每个值代表- -种面 值的货币，每种面值的货币可以使用任意
• 组成aim的最少货币数
• 如果无解，请返回-1

就是上述凑零钱问题，具体解决方案：动态规划
具体步骤：
step1: 可以用dp[i]表示要凑出元钱需要最小的货币数。
step2:一开始都设置为最大值aim + 1,因此货币最小1元，即货币数不会超过aim.
step3:初始化dp[0]= 0。
step 4:后续遍历1元到aim元，枚举每种面值的货币都可能组成的情况，取每次的最小值即可，转移方程为dp[i] = min(dp[i],dp[i - arr[]] + 1).
step 5:最后比较dp[aim]的值是否超过aim,如果超过说明无解，否则返回即可。

 public int minMoney (int[] arr, int aim) {
    
        // write code here
        if(aim < 1) return 0; 
        // 设置最大值aim+1，货币数不会超过aim
        int [] dp = new int[aim+1];
        // dp[i]表示凑齐i元需要多少货币数
        Arrays.fill(dp,aim+1);
        // 初始化
        dp[0] = 0;
        for(int i=1; i<= aim;i++){
    
            for(int j =0 ; j< arr.length; j++){
    
                if(arr[j] <= i) // 如果面值不超过要凑的钱才能用
                    dp[i] = Math.min(dp[i],dp[i-arr[j]]+1);
            }
        }
        return dp[aim] > aim ? -1:dp[aim];   
    }

复杂度分析:
●时间复杂度: O(n.aim), 第一层遍历枚举1元到aim元，第二层遍历枚举n种货币面值
●空间复杂度: O(aim), 辅助数组dp的大小

3、最小花费爬楼梯

题目描述：给定一个整数数组 cost ，其中 cost[i] 是从楼梯第i 个台阶向上爬需要支付的费用，下标从0开始。一旦你支付此费用，即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。

示例
输入：[1,100,1,1,1,90,1,1,80,1]
返回值：6
说明：
你将从下标为 0 的台阶开始。
1.支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
2.支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
3.支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
4.支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
5.支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
6.支付 1 ，向上爬一个台阶，到达楼梯顶部。
总花费为 6 。

思路：动态规划
题目同样考察斐波那契数列的动态规划实现，不同的是题目要求了最小的花费，因此我们将方案统计进行递推的时候只记录最小的开销方案即可。

具体步骤：
step 1：可以用一个数组记录每次爬到第i阶楼梯的最小花费，然后每增加一级台阶就转移一次状态，最终得到结果。
step 2：（初始状态） 因为可以直接从第0级或是第1级台阶开始，因此这两级的花费都直接为0.
step 3：（状态转移） 每次到一个台阶，只有两种情况，要么是它前一级台阶向上一步，要么是它前两级的台阶向上两步，因为在前面的台阶花费我们都得到了，因此每次更新最小值即可，转移方程为：dp[i]=min(dp[i−1]+cost[i−1],dp[i−2]+cost[i−2])

public int minCostClimbingStairs (int[] cost) {
    
        // 总楼梯数,dp[i]表示爬到第i阶需要最小花费
        int[] dp = new int[cost.length+1];
        for(int i = 2; i<= cost.length;i++){
    
            dp[i] = Math.min(dp[i-1] + cost[i-1],dp[i-2]+cost[i-2]);
        }
        return dp[cost.length];
    }

4、最长公共子序列(二)

给定两个字符串str1和str2，输出两个字符串的最长公共子序列。如果最长公共子序列为空，则返回"-1"。目前给出的数据，仅仅会存在一个最长的公共子序列

输入：“1A2C3D4B56”,“B1D23A456A”
返回值：“123456”

解题思路：动态规划

1、思路分析

公共序列
要找s1和s2的公共序列,如果有字符相等s1[i] == s2[j],那么s1[0…i-1]和s2[0…j-1]的公共序列加上相等的字符,就能得到一个更长的公共序列, 所以有, 令s[i][j]表示分别匹配到i,j的一个公共序列

for(int i = 0; i < s1.length();i++){
    
    for(int j = 0;j < s2.length();j++){
    
        if(s1[i] == s2[j]){
     // 匹配字符
            s[i][j] = s[i-1][j-1] + s1[i]; // 上一个拼接 新字符
        }else{
     // 不匹配时
            s[i][j] = s[i][j-1] or s[i-1][j]; // 两个中任选一个
        }
    }
}

最长
上述的方案中,保证了是公共的序列,但是没有控制最长

考虑增加长度的比较,来选择更优长度的s

for(int i = 0; i < s1.length();i++){
    
    for(int j = 0;j < s2.length();j++){
    
        if(s1[i] == s2[j]){
     // 匹配字符
            if(s[i-1][j-1].length() + 1 > s[i][j].length()){
     // 更长
            	s[i][j] = s[i-1][j-1] + s1[i]; // 上一个拼接 新字符
            }
        }else{
     // 不匹配时
            if(s[i][j-1].length() > s[i][j].length()){
     // 更长
                s[i][j] = s[i][j-1];
            }
            if(s[i-1][j].length() > s[i][j].length()){
     // 更长
                s[i][j] = s[i-1][j];
            }
        }
    }
}

空间优化
上述方案的缺点是,把字符串复制了一次又一次,总复杂度达到了O(n3)

既然只有在s1[i]==s2[j]时才增加字符, 所以考虑, 记录上述每个s的上一个s的坐标, 这样最终需要答案时,直接沿着坐标关系,相等时输出即可

边界处理

这里主要的边界是运算时的边界,所以初始化其中一个长度为0时的dp为零

for(int i = 0;i<=s1.size();i++){
     
    dp[i][0] = 0;
}
for(int i = 0;i<=s2.size();i++){
    
    dp[0][i] = 0;
}

=========================================================================
如果已经给定A和B，我们可以用LCS(x, y)表示A和B的LCS长度，下面我们求递归关系式.
1、

2、如果A和B尾部字符相同

3、如果不相同

4.递推公式的边界

5.完整的递推公式

具体步骤：
step 1：优先检查特殊情况。
step 2：获取最长公共子序列的长度可以使用动态规划，我们以dp[i][j]dp[i][j]dp[i][j]表示在s1中以iii结尾，s2中以jjj结尾的字符串的最长公共子序列长度。
step 3：遍历两个字符串的所有位置，开始状态转移：若是iii位与jjj位的字符相等，则该问题可以变成1+dp[i−1][j−1]1+dp[i-1][j-1]1+dp[i−1][j−1]，即到此处为止最长公共子序列长度由前面的结果加1。
step 4：若是不相等，说明到此处为止的子串，最后一位不可能同时属于最长公共子序列，毕竟它们都不相同，因此我们考虑换成两个子问题，dp[i][j−1]dp[i][j-1]dp[i][j−1]或者dp[i−1][j]dp[i-1][j]dp[i−1][j]，我们取较大的一个就可以了，由此感觉可以用递归解决。
step 5：但是递归的复杂度过高，重复计算了很多低层次的部分，因此可以用动态规划，从前往后加，由此形成一个表，表从位置1开始往后相加，正好符合动态规划的转移特征。
step 6：因为最后要返回该序列，而不是长度，所以在构造表的同时要以另一个二维矩阵记录上面状态转移时选择的方向，我们用1表示来自左上方，2表示来自左边，3表示来自上边。
step 7：获取这个序列的时候，根据从最后一位开始，根据记录的方向，不断递归往前组装字符，只有来自左上的时候才添加本级字符，因为这种情况是动态规划中两个字符相等的情况，字符相等才可用。

import java.util.*;

public class Solution {
    
    /** * longest common subsequence * @param s1 string字符串 the string * @param s2 string字符串 the string * @return string字符串 */
    private String x = "";
    private String y = "";
    
    // 获取最长子序列
    private String ans(int i,int j,int[][] b){
    
        String res = "";
        // 递归终止条件
        if(i==0 || j==0)
            return res;
        // 根据方向，向前递归，添加字符
        if(b[i][j] == 1){
    
            res += ans(i - 1, j - 1, b);
            res += x.charAt(i - 1);
        }
        else if(b[i][j] == 2)
            res += ans(i - 1, j, b);
        else if(b[i][j] == 3)
            res += ans(i,j - 1, b);
        return res;
    }
    
    
    public String LCS (String s1, String s2) {
    
        // write code here
        if(s1.length() == 0 || s2.length() == 0)
            return "-1";
        int len1 = s1.length();
        int len2 = s2.length();
        x = s1;
        y = s2;
        // dp[i][j]表示第一个字符串第i位，第二个字符串第j位表示最长公共子序列长度
        int [][] dp = new int[len1 + 1][len2 + 1];
        // 动态规划相加的方向
        int [][] b = new int[len1 + 1][len2 + 1];
        // 遍历两个位置求的最长长度
        for(int i = 1; i<=len1; i++){
    
            for(int j = 1;j <=len2; j++){
    
                if(s1.charAt(i-1) == s2.charAt(j - 1)){
    
                    // 考虑二者向前进一位
                    dp[i][j] = dp[i -1][j-1]+1;
                    b[i][j] = 1;
                }
                // 两个字符不同
                else{
    
                    // 左边的选择更大,即第一个字符串后退一位
                    if(dp[i-1][j] > dp[i][j-1]){
    
                        dp[i][j] = dp[i-1][j];
                        // 左边
                        b[i][j] = 2;
                    }
                    // 右边的选择更大,即第二个字符串后退一位
                    else{
    
                        dp[i][j] = dp[i][j-1];
                        // 来自上方
                        b[i][j] = 3;
                    }
                }
            }
        }
        // 获取答案字符串
        String res = ans(len1,len2,b);
        // 检查答案是否为空
        if(res.isEmpty())
            return "-1";
        else
            return res; 
    }
}

5、最长公共子串

题目描述:给定两个字符串str1和str2,输出两个字符串的最长公共子串
题目保证str1和str2的最长公共子串存在且唯一

输入： “1AB2345CD”,“12345EF”
返回值： “2345”

注意区分最长公共子串 和最长公共子序列：子序列可以是不连续的，但子串一定是连续的。

动态规划

定义dp[i][j]表示字符串str1中第i个字符和str2种第j个字符为最后一个元素所构成的最长公共子串。如果要求dp[i][j]，也就是str1的第i个字符和str2的第j个字符为最后一个元素所构成的最长公共子串，我们首先需要判断这两个字符是否相等。

• 如果不相等，那么他们就不能构成公共子串，也就是dp[i][j]=0;
• 如果相等，我们还需要计算前面相等字符的个数，其实就是dp[i-1][j-1]，所以dp[i][j]=dp[i-1][j-1]+1;
  
  有了递推公式，代码就比较简单了，我们使用两个变量，一个记录最长的公共子串，一个记录最长公共子串的结束位置，最后再对字符串进行截取即可，来看下代码

具体步骤：
step 1：我们可以用dp[i][j]表示在str1中以第i个字符结尾在str2中以第j个字符结尾时的公共子串长度，
step 2：遍历两个字符串填充dp数组，转移方程为：如果遍历到的该位两个字符相等，则此时长度等于两个前一位长度+1，dp[i][j]=dp[i−1][j−1]+1，如果遍历到该位时两个字符不相等，则置为0，因为这是子串，必须连续相等，断开要重新开始。
step 3：每次更新dp[i][j]后，我们维护最大值，并更新该子串结束位置。
step 4：最后根据最大值结束位置即可截取出子串。

import java.util.*;


public class Solution {
    
    /** * longest common substring * @param str1 string字符串 the string * @param str2 string字符串 the string * @return string字符串 */
    public String LCS (String str1, String str2) {
    
        // 记录长度
        int maxlength = 0;
        int maxLastIndex = 0;
        int [][] dp = new int[str1.length() + 1][str2.length() + 1];
        for(int i = 0; i< str1.length();i++){
    
            for(int j = 0; j < str2.length();j++){
    
                if(str1.charAt(i) == str2.charAt(j)){
    
                    dp[i+1][j+1] = dp[i][j]+1;
                    //如果遇到了更长的子串，要更新，记录最长子串的长度，
                    //以及最长子串最后一个元素的位置
                    if(dp[i+1][j+1] > maxlength){
    
                        maxlength = dp[i+1][j+1];
                        maxLastIndex = i;
                    }
                } else{
    
                    //递推公式，两个字符不相等的情况
                    dp[i+1][j+1] = 0;
                }
            }
        }
        //最字符串进行截取，substring(a,b)中a和b分别表示截取的开始和结束位置
        return str1.substring(maxLastIndex - maxlength + 1, maxLastIndex + 1);
        
    }
}

6、不同路径的数目(一)

题目描述：一个机器人在m×n大小的地图的左上角（起点）。
机器人每次可以向下或向右移动。机器人要到达地图的右下角（终点）。
可以有多少种不同的路径从起点走到终点？

示例
输入：2,1
返回值：1
输入：2,2
返回值：2

递归

具体做法:
首先我们在左上角第一个格子的时候，有两种行走方式:如果向右走，相当于后面在一个(n - 1) * m的矩阵中查找从左上角到右下角的不同路径数;而如果向下走，相当于后面在一个n * (m - 1)的矩阵中查找从左上角到右下角不同的路径数。而(n - 1) * m的矩阵与n * (m - 1)的矩阵都是n *m矩阵的子问题，因此可以使用递归。
step 1:(终止条件)当矩阵变长n减少到1的时候，很明显只能往下走，没有别的选择了，只有1条路径;同理m减少到1时也是如此。因此此时返回数量为1.
step 2:(返回值)对于每一级都将其两个子问题返回的结果相加返回给上一级。
step 3:(本级任务)每一级都有向下或者向右两种路径选择，分别进入相应分支的子问题。

public int uniquePaths (int m, int n) {
    
        // 递归
        if(m ==1 || n == 1){
    
            return 1;
        }
        // 向下 (m-1) * n 向右 m *(n-1) 
        return uniquePaths(m-1,n) + uniquePaths(m , n-1);
    }

复杂度分析:

• 时间复杂度:O(mn)，其中m、n分别为矩阵的两边长，递归过程对于每个m最多都要经过每一种n
• 空间复杂度:O(mn)，递归栈的最大深度

动态规划

如果我们此时就在右下角的格子，那么能够到达该格子的路径只能是它的上方和它的左方两个格子，因此从左上角到右下角的路径数应该是从左上角到它的左边格子和上边格子的路径数之和，因此可以动态规划。
step 1:用dp [i][j]表示大小为i* j的矩阵的路径数量，下标从1开始。
step 2:(初始条件)当i或者j为1的时候，代表矩阵只有一行或者一列，因此只有一种路径。
step 3:（转移方程)每个格子的路径数只会来自它左边的格子数和上边的格子数，因此状态转移为dp[i][j] = dp[i -1][j]＋dp[i][j-1]。

public int uniquePaths (int m, int n) {
    
        // 动态规划
        //dp[i][j]表示⼤⼩为i*j的矩阵的路径数量
        int[][] dp = new int[m+1][n+1];
        for(int i = 1;i <= m;i++){
    
            for(int j = 1 ; j<=n; j++){
    
                if(i==1 || j ==1){
    
                    dp[i][j]=1;
                    continue;
                }
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m][n];
    }

复杂度分析:

• 时间复杂度:O(n)，计算过程需要从1遍历到n
• 空间复杂度:O(1)，常数级变量，无额外辅助空间

7、矩阵的最小路径和

题目描述：给定一个 n * m 的矩阵 a，从左上角开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，输出所有的路径中最小的路径和。

例如：当输入[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]时，对应的返回值为12，
所选择的最小累加和路径如下图所示：

示例1
输入：[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]
返回值：12
示例2
输入：[[1,2,3],[1,2,3]]
返回值：7

动态规划

设计思想:

定义一个dp大小为n×m矩阵，其中 dp[i][j]的值代表走到(i,j)的最小路径和。
当i = 0, j = 0时，dp[i][j] = matrix [i][j]
当i = 0，j != 0时， dp[i][j] = dp[0][j-1] +matrix[0][j]
当i != 0，j = 0时, dp[i][j] = dp[i-1][0] +matrix[i][0]
当i != 0， j != 0时, dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j]最后返回值为dp[n-1][m-1]。
最后返回值 dp[n-1][m-1]

具体步骤：
step 1:我们可以构造一个与矩阵同样大小的二维辅助数组，其中dp[][j]表示以(i,j)位置为终点的最短路径和，则dp[0][0]= matria[0][0]。
step 2:很容易知道第一行与第一列，只能分别向右或向下，没有第二种选择，因此第一行只能由其左边的累加，第—列只能由其上面的累加。
step 3:边缘状态构造好以后，遍历矩阵，补全矩阵中每个位置的dp数组值:如果当前的位置是(i，j)，上一步要么是(i-1,j)往下，要么就是(i,j一1)往右，那么取其中较小值与当前位置的值相加就是到当前位置的最小路径和，因此状态转移公式为dp[i][j]=min(dp[i -1][j], dp[i][j-1])+matria[i][i]。
step 4:最后移动到(n - 1, m —1)的位置就是到右下角的最短路径和。

public int minPathSum (int[][] matrix) {
    
        // 行、 列
        int n = matrix.length;
        int m = matrix[0].length;
        int[][] dp = new int[n+1][m+1];
        dp[0][0] = matrix[0][0]; // dp[i][j] 表示以i，j位置为终点的最短路径长度
        for(int i =1;i<n;i++) // 处理第一列
            dp[i][0] = matrix[i][0] + dp[i-1][0];
        for(int i =1;i<m;i++) // 处理第一行
            dp[0][i] = matrix[0][i] + dp[0][i-1];
        for(int i = 1; i< n;i++){
    
            for(int j = 1; j<m;j++){
    
                dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + matrix[i][j];
            }
        }
        return dp[n-1][m-1];

8、把数字翻译成字符串

题目描述：有一种将字母编码成数字的方式：‘a’->1, ‘b->2’, … , ‘z->26’。
我们把一个字符串编码成一串数字，再考虑逆向编译成字符串。
由于没有分隔符，数字编码成字母可能有多种编译结果，例如 11 既可以看做是两个 ‘a’ 也可以看做是一个 ‘k’ 。但 10 只可能是 ‘j’ ，因为 0 不能编译成任何结果。
现在给一串数字，返回有多少种可能的译码结果

输入：“12”
返回值：2
说明：2种可能的译码结果（”ab” 或”l”）

输入： “31717126241541717”
返回值： 192
说明： 192种可能的译码结果

动态规划

对于普通数组1-9，译码方式只有一种，但是对于11-19，21-26，译码方式有可选择的两种方案，因此我们使用动态规划将两种方案累计。

具体步骤：
step 1：用辅助数组dp表示前i个数的译码方法有多少种
step 2：对于一个数，我们可以直接译码它，也可以将其与前面的1或者2组合起来译码：如果直接译码，则dp[i]=dp[i−1]；如果组合译码，则dp[i]=dp[i−2]
step 3：对于只有一种译码方式的，选上种dp[i−1]即可，对于满足两种译码方式（10，20不能）则是dp[i−1]+dp[i−2]
step 4：依次相加，最后的dp[length]即为所求答案。

public class Solution {
    
    /** * 解码 * @param nums string字符串 数字串 * @return int整型 */
    public int solve (String nums) {
    
        // 动态规划
        if(nums.equals("0"))
            return 0;
        if(nums.equals("10")|| nums.equals("20"))
            return 1;
        // 当0的前面不是1和2
        for(int i=1;i<nums.length();i++){
    
            if(nums.charAt(i) =='0')
                if(nums.charAt(i-1) !='1' && nums.charAt(i-1) !='2')
                    return 0;
        }
        int [] dp = new int[nums.length()+1];
        //初始化辅助数组1
        Arrays.fill(dp,1);
        for(int i=2; i<=nums.length();i++){
    
            if(nums.charAt(i-2) == '1' && nums.charAt(i-1) !='0' || nums.charAt(i-2) == '2' && nums.charAt(i-1) >'0'&& nums.charAt(i-1) <'7' )
                dp[i] = dp[i-1] + dp[i-2];
            else
                dp[i] = dp[i-1];
            
        }
        return dp[nums.length()];
    }
}

9、最长上升子序列(一)

题目描述：给定一个长度为 n 的数组 arr，求它的最长严格上升子序列的长度。
所谓子序列，指一个数组删掉一些数（也可以不删）之后，形成的新数组。例如 [1,5,3,7,3] 数组，其子序列有：[1,3,3]、[7] 等。但 [1,6]、[1,3,5] 则不是它的子序列。

输入：[6,3,1,5,2,3,7]
返回值：4
说明：该数组最长上升子序列为 [1,2,3,7] ，长度为4

动态规划

要找到最长的递增子序列长度，每当我们找到一个位置，它是继续递增的子序列还是不是，它选择前面哪一处接着才能达到最长的递增子序列，这类有状态转移的问题常用方法是动态规划。
具体步骤：
step 1：用dp[i]表示到元素iii结尾时，最长的子序列的长度，初始化为1，因为只有数组有元素，至少有一个算是递增。
step 2：第一层遍历数组每个位置，得到n个长度的子数组。
step 3：第二层遍历相应子数组求对应到元素iii结尾时的最长递增序列长度，期间维护最大值。
step 4：对于每一个到iii结尾的子数组，如果遍历过程中遇到元素j小于结尾元素，说明以该元素结尾的子序列加上子数组末尾元素也是严格递增的，因此转移方程为dp[i]=dp[j]+1。

public int LIS (int[] arr) {
    
        // 动态规划
        int[] dp = new int[arr.length +1];
        Arrays.fill(dp,1);
        int res = 0;
        for(int i=1;i< arr.length;i++){
    
            for(int j=0;j<i;j++){
    
                if(arr[i]> arr[j] && dp[i]< dp[j]+1){
    
                    dp[i] = dp[j]+1;
                    res = Math.max(res, dp[i]);
                }
            }
        }
        return res;
    }

10、连续子数组的最大和

题目描述：输入一个长度为n的整型数组array，数组中的一个或连续多个整数组成一个子数组，子数组最小长度为1。求所有子数组的和的最大值。

示例
输入：[1,-2,3,10,-4,7,2,-5]
返回值：18
说明：经分析可知，输入数组的子数组[3,10,-4,7,2]可以求得最大和为18

解题思路：因为数组中有正有负有0，因此每次遇到一个数，要不要将其加入我们所求的连续子数组里面，是个问题，有可能加入了会更大，有可能加入了会更小，而且我们要求连续的最大值，因此这类有状态转移的问题可以考虑动态规划。

具体步骤：
step 1：可以用dp数组表示以下标iii为终点的最大连续子数组和。
step 2：遍历数组，每次遇到一个新的数组元素，连续的子数组要么加上变得更大，要么这个元素本身就更大，要么会更小，更小我们就舍弃，因此状态转移为dp[i]=max(dp[i−1]+array[i],array[i])
step 3：因为连续数组可能会断掉，每一段只能得到该段最大值，因此我们需要维护一个最大值。

import java.util.*;

public class Solution {
    
    public int FindGreatestSumOfSubArray(int[] array) {
    
        // 动态规划
        int[] dp = new int[array.length +1];
        int res = array[0];
        dp[0] = array[0];
        for(int i=1;i < array.length;i++){
    
            dp[i] = Math.max(dp[i-1] + array[i], array[i]);
            // 保存出现的最大值
            res = Math.max(res,dp[i]);
        }
        return res;
    }
}

11、最长回文子串

题目描述：对于长度为n的一个字符串A（仅包含数字，大小写英文字母），请设计一个高效算法，计算其中最长回文子串的长度。

示例
输入：“ababc”
返回值：3
说明：最长的回文子串为"aba"与"bab"，长度都为3

贪心思想属于动态规划思想中的一种，其基本原理是找出整体当中给的每个局部子结构的最优解，并且最终将所有的这些局部最优解结合起来形成整体上的一个最优解。

思路：回文串，有着左右对称的特征，从首尾一起访问，遇到的元素都是相同的。但是我们这里正是要找最长的回文串，并不事先知道长度，怎么办？判断回文的过程是从首尾到中间，那我们找最长回文串可以逆着来，从中间延伸到首尾，这就是中心扩展法。

具体步骤：
step 1：遍历字符串每个字符。
step 2：以每次遍历到的字符为中心（分奇数长度和偶数长度两种情况），不断向两边扩展。
step 3：如果两边都是相同的就是回文，不断扩大到最大长度即是以这个字符（或偶数两个）为中心的最长回文子串。
step 4：我们比较完每个字符为中心的最长回文子串，取最大值即可。

import java.util.*;


public class Solution {
    
    /** * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可 * * * @param A string字符串 * @return int整型 */
    
    // 中心点开始扩展
    private int fun(String s, int begin,int end){
    
        while(begin >= 0 && end < s.length() && s.charAt(begin) == s.charAt(end)){
    
            begin--;
            end ++;
        }
        return end - begin -1;
    }
  
    public int getLongestPalindrome (String A) {
    
        // 中心扩展法
        int [] dp = new int[A.length()+1];
        int maxlen = 1;
        // 一开始值都设置为1
        Arrays.fill(dp,1);
        for(int i=0;i<A.length()-1;i++){
    
            //分奇数长度和偶数长度向两边扩展
            dp[i] = Math.max(dp[i],Math.max(fun(A,i,i),fun(A,i,i+1))); 
            // 保存最大值
            maxlen = Math.max(maxlen,dp[i]);
        }
        return maxlen;
    }
}

精简版本---其实不需要dp

```java
import java.util.*;
public class Solution {
    
    public int fun(String s, int begin, int end){
    
        //每个中心点开始扩展
        while(begin >= 0 && end < s.length() && s.charAt(begin) == s.charAt(end)){
     
            begin--;
            end++;
        }
        //返回长度
        return end - begin - 1; 
    } 
    public int getLongestPalindrome (String A) {
    
        int maxlen = 1;
        //以每个点为中心
        for(int i = 0; i < A.length() - 1; i++) 
            //分奇数长度和偶数长度向两边扩展
            maxlen = Math.max(maxlen, Math.max(fun(A, i, i), fun(A, i, i + 1))); 
        return maxlen;
    }
}

12、数字字符串转化成IP地址

题目描述：现在有一个只包含数字的字符串，将该字符串转化成IP地址的形式，返回所有可能的情况。
例如：
给出的字符串为"25525522135",
返回[“255.255.22.135”, “255.255.221.35”]. (顺序没有关系)

枚举

思路：对于IP字符串，如果只有数字，则相当于需要我们将IP地址的三个点插入字符串中，而第一个点的位置只能在第一个字符、第二个字符、第三个字符之后，而第二个点只能在第一个点后1-3个位置之内，第三个点只能在第二个点后1-3个位置之内，且要要求第三个点后的数字数量不能超过3，因为IP地址每位最多3位数字。

具体做法：
step 1：依次枚举这三个点的位置。
step 2：然后截取出四段数字。
step 3：比较截取出来的数字，不能大于255，且除了0以外不能有前导0，然后才能组装成IP地址加入答案中。

 public ArrayList<String> restoreIpAddresses (String s) {
    
        // 暴力解法--枚举
        ArrayList<String> res = new ArrayList<>();
        int n = s.length();
        // 遍历第一个点
        for(int i =1; i<4 && i< n-2; i++){
    
            // 第二个点
            for(int j = i+1; j< i+4 && j < n-1;j++){
    
                //第三个点
                for(int k = j+1; k < j+4 && k < n; k++){
    
                    // 最后一段剩余数字不超过3
                    if(n-k >=4)
                        continue;
                    // 截取
                    String a = s.substring(0,i);
                    String b = s.substring(i,j);
                    String c = s.substring(j,k);
                    String d = s.substring(k);
                    
                    // 判断数字不大于255
                    if(Integer.parseInt(a) > 255 ||Integer.parseInt(b) > 255 ||Integer.parseInt(c) > 255||Integer.parseInt(d) > 255)
                        continue;
                    // 排除前导0
                    if((a.length() != 1 && a.charAt(0) == '0') || (b.length() != 1 && b.charAt(0) == '0') ||  (c.length() != 1 && c.charAt(0) == '0') || (d.length() != 1 && d.charAt(0) == '0'))
                        continue;
                    //组装
                    String temp = a + "." + b + "."+ c + "." + d;
                    res.add(temp);
                }
            }
        }
        return res;
    }

递归+ 回溯

递归是一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。因此递归过程，最重要的就是查看能不能讲原本的问题分解为更小的子问题，这是使用递归的关键。

思路：对于IP地址每次取出一个数字和一个点后，对于剩余的部分可以看成是一个子问题，因此可以使用递归和回溯剪枝将点插入数字中。

import java.util.*;

public class Solution {
    
    /** * * @param s string字符串 * @return string字符串ArrayList */
    ArrayList<String> res = new ArrayList<>();
    ArrayList<String> ip = new ArrayList<>();
   
    public ArrayList<String> restoreIpAddresses (String s) {
    
        // write code here
        dfs(s, 0);
        return res;
    }
    
    public void dfs(String s , int start){
    
        if(ip.size() == 4 && start == s.length()){
    
            // 合法解
            res.add(ip.get(0) + '.' + ip.get(1) + '.' + ip.get(2) + '.'+ ip.get(3));
            return;
        }
        if(s.length() - start > 3 *(4 - ip.size())) // 剪枝，剪去总长度大于12，或者是每小段大于3
            return;
        if(s.length() - start < (4- ip.size())) // 剪枝，剪去总长度小于4，或者是每小段小于0
            return;
        int num = 0;
        for(int i= start; i< start + 3 && i<s.length(); i++){
    
            num = num * 10 + (s.charAt(i) - '0'); // ip每一段的值
            if(num < 0 || num > 255)
                continue;
            ip.add(s.substring(start, i+1));
            
            dfs(s, i+1);
            ip.remove(ip.size() -1);
    
            if(num == 0) // 不允许前缀0
                break;
        }
        
    }
}

13、编辑距离(一)

题目描述：给定两个字符串 str1 和 str2 ，请你算出将 str1 转为 str2 的最少操作数。
你可以对字符串进行3种操作：
1.插入一个字符
2.删除一个字符
3.修改一个字符。

示例1
输入：“nowcoder”,“new”
返回值：6
说明：“nowcoder”=>“newcoder”(将’o’替换为’e’)，修改操作1次"nowcoder"=>“new”(删除"coder")，删除操作5次
示例2
输入：“intention”,“execution”
返回值：5
说明：一种方案为:因为2个长度都是9，后面的4个后缀的长度都为"tion"，于是从"inten"到"execu"逐个修改即可

动态规划

思路：把第一个字符串变成第二个字符串，我们需要逐个将第一个字符串的子串最少操作下变成第二个字符串，这就涉及了第一个字符串增加长度，状态转移，那可以考虑动态规划。用dp[i][j]表示从两个字符串首部各自到str1[i]和str2[j]为止的子串需要的编辑距离，那很明显dp[str1.length][str2.length]就是我们要求的编辑距离。（下标从1开始）

具体步骤：
step 1：初始条件： 假设第二个字符串为空，那很明显第一个字符串子串每增加一个字符，编辑距离就加1，这步操作是删除；同理，假设第一个字符串为空，那第二个字符串每增加一个字符，编剧距离就加1，这步操作是添加。
step 2：状态转移： 状态转移肯定是将dp矩阵填满，那就遍历第一个字符串的每个长度，对应第二个字符串的每个长度。如果遍历到str1[i]和 str2[j]的位置，这两个字符相同，这多出来的字符就不用操作，操作次数与两个子串的前一个相同，因此有dp[i][j]=dp[i−1][j−1]；如果这两个字符不相同，那么这两个字符需要编辑，但是此时的最短的距离不一定是修改这最后一位，也有可能是删除某个字符或者增加某个字符，因此我们选取这三种情况的最小值增加一个编辑距离，即dp[i][j]=min(dp[i−1][j−1],min(dp[i−1][j],dp[i][j−1]))+1。
图示：

 public int editDistance (String str1, String str2) {
    
        // 使用动态规划
        int n1 = str1.length();
        int n2 = str2.length();
        // 设置dp[i][j],表示从两个字符串首部各自到str1[i]和str2[j]为止的子串需要的编辑距离
        int[][] dp = new int[n1+1][n2+1];
        // 判断边界条件，假设第二字符串为空
        for(int i = 1 ; i<= n1;i++)
            dp[i][0] = dp[i-1][0] +1;
        // 判断边界条件，假设第一个字符串为空
        for(int i = 1 ; i<= n2;i++)
            dp[0][i] = dp[0][i-1] +1;
        // 除去初始化边界外
        for(int i=1;i<=n1;i++){
    
            for(int j=1;j<=n2;j++){
    
                // 进行状态转移，判断两个字符串是否相等,如果相等，字符就不用操作
                if(str1.charAt(i-1) == str2.charAt(j-1))
                    dp[i][j] = dp[i-1][j-1];
                else
                    dp[i][j] = Math.min(dp[i-1][j-1],Math.min(dp[i-1][j],dp[i][j-1]))+1; 
            }
        }
        return dp[n1][n2];
    }

14、正则表达式匹配

题目描述：请实现一个函数用来匹配包括’.‘和’‘的正则表达式。
1.模式中的字符’.‘表示任意一个字符
2.模式中的字符’'表示它前面的字符可以出现任意次（包含0次）。
在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与模式"a.a"和"abaca"匹配，但是与"aa.a"和"ab*a"均不匹配

示例：
输入：“aaa”,"aa"
返回值：true
说明：中间的可以出现任意次的a，所以可以出现1次a，能匹配上

思路：
如果是只有小写字母，那么直接比较字符是否相同即可匹配，如果再多一个’.‘，可以用它匹配任意字符，只要对应str中的元素不为空就行了。但是多了’*'字符，它的情况有多种，涉及状态转移，因此我们用动态规划。

具体步骤：
step 1：设dp[i][j]表示str前i个字符和pattern前j个字符是否匹配。（需要注意这里的i，j是长度，比对应的字符串下标要多1）

step 2：（初始条件）首先，毋庸置疑，两个空串是直接匹配，因此dp[0][0]=true。然后我们假设str字符串为空，那么pattern要怎么才能匹配空串呢？答案是利用’‘字符出现0次的特性。遍历pattern字符串，如果遇到’'意味着它前面的字符可以出现0次，要想匹配空串也只能出现0，那就相当于考虑再前一个字符是否能匹配，因此dp[0][i]=dp[0][i−2]。

step 3： （状态转移） 然后分别遍历str与pattern的每个长度，开始寻找状态转移。首先考虑字符不为’‘的简单情况，只要遍历到的两个字符相等，或是pattern串中为’.‘即可匹配，因此最后一位匹配，即查看二者各自前一位是否能完成匹配，即dp[i][j]=dp[i−1][j−1]。然后考虑’'出现的情况：

• pattern[j - 2] == ‘.’ || pattern[j - 2] == str[i -1]：即pattern前一位能够多匹配一位，可以用’*'让它多出现一次或是不出现，因此有转移方程dp[i][j]=dp[i−1][j]∣∣dp[i][j−2]
• 不满足上述条件，只能不匹配，让前一个字符出现0次，dp[i][j]=dp[i][j−2]
  

import java.util.*;
public class Solution {
    
    public boolean match (String str, String pattern) {
    
        int n1 = str.length();
        int n2 = pattern.length();
        //dp[i][j]表示str前i个字符和pattern前j个字符是否匹配
        boolean[][] dp = new boolean[n1 + 1][n2 + 1]; 
        //遍历str每个长度
        for(int i = 0; i <= n1; i++){
      
            //遍历pattern每个长度
            for(int j = 0; j <= n2; j++){
     
                //空正则的情况
                if(j == 0){
     
                    dp[i][j] = (i == 0 ? true : false);
                //非空的情况下 星号、点号、字符
                }else{
     
                    if(pattern.charAt(j - 1) != '*'){
    
                        //当前字符不为*，用.去匹配或者字符直接相同
                        if(i > 0 && (str.charAt(i - 1) == pattern.charAt(j - 1) || pattern.charAt(j - 1) == '.')){
    
                            dp[i][j] = dp[i - 1][j - 1];
                        }
                    }else{
    
                        //碰到*
                        if(j >= 2){
    
                            dp[i][j] |= dp[i][j - 2];
                        }
                        //若是前一位为.或者前一位可以与这个数字匹配
                        if(i >= 1 && j >= 2 && (str.charAt(i - 1) == pattern.charAt(j - 2) || pattern.charAt(j - 2) == '.')){
    
                            dp[i][j] |= dp[i - 1][j];
                        }
                    }
                }
            }
        }
        return dp[n1][n2];
  }
}

15、最长的括号子串

题目描述：给出一个长度为 n 的，仅包含字符 ‘(’ 和 ‘)’ 的字符串，计算最长的格式正确的括号子串的长度。

例1: 对于字符串 “(()” 来说，最长的格式正确的子串是 “()” ，长度为 2 .
例2：对于字符串 “)()())” , 来说, 最长的格式正确的子串是 “()()” ，长度为 4 .

对于括号匹配的问题，可以首选栈，通过先进后出的原则进行分析

栈

思路：因为括号需要一一匹配，而且先来的左括号，只能匹配后面的右括号，因此可以考虑使用栈的先进后出功能，使括号匹配。

具体步骤：
step 1：可以使用栈来记录左括号下标。
step 2：遍历字符串，左括号入栈，每次遇到右括号则弹出左括号的下标。
step 3：然后长度则更新为当前下标与栈顶下标的距离。
step 4：遇到不符合的括号，可能会使栈为空，因此需要使用start记录上一次结束的位置，用当前下标减去start即可获取长度，即得到子串。
step 5：循环中最后维护子串长度最大值。

public int longestValidParentheses (String s) {
    
        // 栈
        int res = 0;
        int start = -1;
        Stack<Integer> st = new Stack<Integer>();
        for(int i=0;i<s.length();i++){
    
            //遇到左括号，直接入栈
            if(s.charAt(i)== '(')
                st.push(i);
            // 遇到右括号
            else{
    
                //如果右括号时栈为空，不合法，设置为结束位置
                if(st.isEmpty())
                    start = i;
                else{
    
                    // 弹出左括号
                    st.pop();
                    if(!st.empty())
                        //栈中还有左括号，说明右括号不够，减去栈顶位置就是长度
                        res = Math.max(res, i - st.peek());
                    else
                        res = Math.max(res, i- start);   
                }
            } 
        }
        return res; 
    }

动态规划

子串长度的问题，涉及状态转移，直接用动态规划的方法
具体做法：
step 1：用dp[i]dp[i]dp[i]表示以下标为i的字符为结束点的最长合法括号长度。
step 2：很明显知道左括号不能做结尾，因此但是左括号都是dp[i]=0dp[i]=0dp[i]=0。
step 3：我们遍历字符串，因为第一位不管是左括号还是右括号dp数组都是0，因此跳过，后续只查看右括号的情况，右括号有两种情况：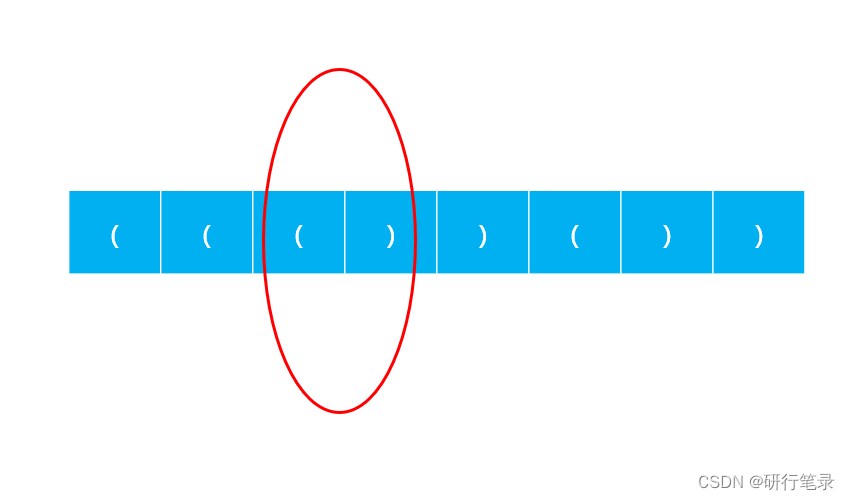

如图所示，左括号隔壁是右括号，那么合法括号需要增加2，可能是这一对括号之前的基础上加，也可能这一对就是起点，因此转移公式为：dp[i]=(i>=2?dp[i−2]:0)+2

如图所示，与该右括号匹配的左括号不在自己旁边，而是它前一个合法序列之前，因此通过下标减去它前一个的合法序列长度即可得到最前面匹配的左括号，因此转移公式为：dp[i]=(i−dp[i−1]>1?dp[i−dp[i−1]−2]:0)+dp[i−1]+2

public int longestValidParentheses (String s) {
    
        // 动态规划
        int res = 0;
        if(s.length() == 0 || s == null)
            return res;
        //dp[i]表示以下标为i的字符为结束点的最长合法括号长度
        int[] dp = new int[s.length()+1];
        //第一位不管是左括号还是右括号都是0，因此不用管
        for(int i=1;i<s.length();i++){
    
            if(s.charAt(i) == ')'){
    
                if(s.charAt(i-1)=='(')
                    dp[i] = (i>=2 ? dp[i-2]:0) +2;
                else if(i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(')
                     dp[i] = (i - dp[i - 1] > 1 ? dp[i - dp[i - 1] - 2] : 0) + dp[i - 1] + 2;
            }
            res = Math.max(res,dp[i]);
        }
        return res;  
    }

16、打家劫舍(一)

题目描述：你是一个经验丰富的小偷，准备偷沿街的一排房间，每个房间都存有一定的现金，为了防止被发现，你不能偷相邻的两家，即，如果偷了第一家，就不能再偷第二家；如果偷了第二家，那么就不能偷第一家和第三家。
给定一个整数数组nums，数组中的元素表示每个房间存有的现金数额，请你计算在不被发现的前提下最多的偷窃金额。

输入： [1,2,3,4]
返回值： 6
说明： 最优方案是偷第 2，4 个房间

思路：或许有人认为利用贪心思想，偷取最多人家的钱就可以了，要么偶数家要么奇数家全部的钱，但是有时候会为了偷取更多的钱，或许可能会连续放弃两家不偷，因此这种方案行不通，我们依旧考虑动态规划。

具体步骤：
step 1：用dp[i]表示长度为i的数组，最多能偷取到多少钱，只要每次转移状态逐渐累加就可以得到整个数组能偷取的钱。
step 2：（初始状态） 如果数组长度为1，只有一家人，肯定是把这家人偷了，收益最大，因此dp[1]=nums[0]。
step 3：（状态转移） 每次对于一个人家，我们选择偷他或者不偷他，如果我们选择偷那么前一家必定不能偷，因此累加的上上级的最多收益，同理如果选择不偷他，那我们最多可以累加上一级的收益。因此转移方程为dp[i]=max(dp[i−1],nums[i−1]+dp[i−2])。这里的i在dp中为数组长度，在nums中为下标。

public int rob (int[] nums) {
    
        // 动态规划
        int [] dp = new int[nums.length+1];
        // 长度为1 ，直接选择第一家
        dp[1] = nums[0];
        for(int i=2;i<=nums.length;i++)
            dp[i] = Math.max(dp[i-1],nums[i-1]+dp[i-2]);
        
        return dp[nums.length];
    }

17、打家劫舍(二)

题目描述：沿湖的房间组成一个闭合的圆形，即第一个房间和最后一个房间视为相邻。
给定一个长度为n的整数数组nums，数组中的元素表示每个房间存有的现金数额，请你计算在不被发现的前提下最多的偷窃金额。
区别：数组是环形的，第一家和最后一家是相邻的，偷了第一家，最后一家就不能偷，反之也是如此。

思路：这道题与打家劫舍(一)比较类似，区别在于这道题是环形，第一家和最后一家是相邻的，既然如此，在原先的方案中第一家和最后一家不能同时取到。

具体步骤：
step 1：使用原先的方案是：用dp[i]表示长度为i的数组，最多能偷取到多少钱，只要每次转移状态逐渐累加就可以得到整个数组能偷取的钱。

step 2：（初始状态） 如果数组长度为1，只有一家人，肯定是把这家人偷了，收益最大，因此dp[1]=nums[0]。

step 3：（状态转移） 每次对于一个人家，我们选择偷他或者不偷他，如果我们选择偷那么前一家必定不能偷，因此累加的上上级的最多收益，同理如果选择不偷他，那我们最多可以累加上一级的收益。因此转移方程为dp[i]=max(dp[i−1],nums[i−1]+dp[i−2])。这里的i在dp中为数组长度，在nums中为下标。

step 4：此时第一家与最后一家不能同时取到，那么我们可以分成两种情况讨论：
情况1：偷第一家的钱，不偷最后一家的钱。初始状态与状态转移不变，只是遍历的时候数组最后一位不去遍历。
情况2：偷最后一家的请，不偷第一家的钱。初始状态就设定了dp[1]=0，第一家就不要了，然后遍历的时候也会遍历到数组最后一位。

step 5：最后取两种情况的较大值即可。

import java.util.*;


public class Solution {
    
    /** * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可 * * * @param nums int整型一维数组 * @return int整型 */
    public int rob (int[] nums) {
    
        // write code here
        int[] dp = new int[nums.length+1];
        // 选择第一家
        dp[1] = nums[0];
        for(int i = 2;i<nums.length;i++){
    
            dp[i] = Math.max(dp[i-1],dp[i-2]+ nums[i-1]);
        }
        int res = dp[nums.length-1];
        // 不选择第一家
        Arrays.fill(dp,0);
        dp[1] = 0;
        for(int i = 2;i<= nums.length;i++){
    
            dp[i] = Math.max(dp[i-1],dp[i-2]+ nums[i-1]);
        }
        return Math.max(res, dp[nums.length]);
        
    }
}

18、买卖股票的最好时机(一)

题目描述：
假设你有一个数组prices，长度为n，其中prices[i]是股票在第i天的价格，请根据这个价格数组，返回买卖股票能获得的最大收益
1.你可以买入一次股票和卖出一次股票，并非每天都可以买入或卖出一次，总共只能买入和卖出一次，且买入必须在卖出的前面的某一天
2.如果不能获取到任何利润，请返回0
3.假设买入卖出均无手续费

示例
输入：[8,9,2,5,4,7,1]
返回值：5
说明：在第3天(股票价格 = 2)的时候买入，在第6天(股票价格 = 7)的时候卖出，最大利润 = 7-2 = 5 ，不能选择在第2天买入，第3天卖出，这样就亏损7了；同时，你也不能在买入前卖出股票

贪心算法

思路：
1、使用变量记录历史最低价格 minprice
2、则在第 i 天卖出股票能得到的利润就是 prices[i] - minprice
3、因此，我们只需要遍历价格数组一遍，记录历史最低点

public int maxProfit (int[] prices) {
    
        // 一次遍历贪心算法
        int res = 0;
        // 特殊情况
        if(prices.length ==0)
            return res;
        // 保持最低价格
        int min = prices[0];
        // 因为min就是第一个位置，所以i直接从1开始
        for(int i=1;i< prices.length;i++){
    
            min = Math.min(min,prices[i]);
            res = Math.max(res, prices[i]- min);
        }
        return res;
    }

动态规划

思路：对于每天有到此为止的最大收益和是否持股两个状态，因此我们可以用动态规划。

具体步骤：
step 1：用dp[i][0]表示第i天不持股到该天为止的最大收益，dp[i][1]表示第i天持股，到该天为止的最大收益。
step 2：（初始状态） 第一天不持股，则总收益为0，dp[0][0]=0；第一天持股，则总收益为买股票的花费，此时为负数，dp[0][1]=−prices[0]。
step 3：（状态转移） 对于之后的每一天，如果当天不持股，有可能是前面的若干天中卖掉了或是还没买，因此到此为止的总收益和前一天相同，也有可能是当天才卖掉，我们选择较大的状态dp[i][0]=max(dp[i−1][0],dp[i−1][1]+prices[i])
step 4：如果当天持股，有可能是前面若干天中买了股票，当天还没卖，因此收益与前一天相同，也有可能是当天买入，此时收益为负的股价，同样是选取最大值：dp[i][1]=max(dp[i−1][1],−prices[i])。

public int maxProfit (int[] prices) {
    
        int n = prices.length;
        //dp[i][0]dp[i][0]dp[i][0]表示第i天不持股到该天为止的最大收益，dp[i][1]dp[i][1]dp[i][1]表示第i天持股，到该天为止的最大收益。
        int [][] dp = new int[n+1][2];
        // 第一天不持股
        dp[0][0] = 0;
        // 第一天持股
        dp[0][1] = -prices[0];
        for(int i=1;i < prices.length;i++){
    
            // 1、前面若干天卖掉，总收益和前一天相同
            // 2、 当天卖掉，总收益为上一天的加上卖掉的
            dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
            // 当天持股:1、还没卖 2、当天买入
            dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
        }
        // 最后一天不持股
        return dp[prices.length-1][0];  
    }

19、买卖股票的最好时机(二)

题目描述：假设你有一个数组prices，长度为n，其中prices[i]是某只股票在第i天的价格，请根据这个价格数组，返回买卖股票能获得的最大收益

1. 你可以多次买卖该只股票，但是再次购买前必须卖出之前的股票
2. 如果不能获取收益，请返回0
3. 假设买入卖出均无手续费

贪心算法

思路：其实我们要想获取最大收益，只需要在低价买入高价卖出就可以了，因为可以买卖多次。利用贪心思想：只要一段区间内价格是递增的，那么这段区间的差值就是我们可以有的收益。
具体步骤:
step 1：遍历数组，只要数组后一个比前一个更大，就可以有收益。
step 2：将收益累加，得到最终结果。

public int maxProfit (int[] prices) {
    
        // write code here
        int res = 0;
        for(int i=1;i < prices.length;i++){
    
            if(prices[i-1] < prices[i])
                res += prices[i] - prices[i-1];
        }
        return res;
    }

动态规划

与上题区别是可以进行多次买入卖出

思路： 但是对于每天还是有到此为止的最大收益和是否持股两个状态，因此我们照样可以用动态规划。

step 1：用dp[i][0]表示第i天不持股到该天为止的最大收益，dp[i][1]dp[i][1]dp[i][1]表示第i天持股，到该天为止的最大收益。
step 2：（初始状态） 第一天不持股，则总收益为0，dp[0][0]=0dp[0][0]=0dp[0][0]=0；第一天持股，则总收益为买股票的花费，此时为负数，dp[0][1]=−prices[0]。
step 3：（状态转移） 对于之后的每一天，如果当天不持股，有可能是前面的若干天中卖掉了或是还没买，因此到此为止的总收益和前一天相同，也有可能是当天卖掉股票，我们选择较大的状态dp[i][0]=max(dp[i−1][0],dp[i−1][1]+prices[i])；
step4：如果当天持股，可能是前几天买入的还没卖，因此收益与前一天相同，也有可能是当天买入，减去买入的花费，同样是选取最大值：dp[i][1]=max(dp[i−1][1],dp[i−1][0]−prices[i]))

跟上题目区别在于当天持股情况：最大值dp[i][1]=max(dp[i−1][1],dp[i−1][0]−prices[i]))

public int maxProfit (int[] prices) {
    
        // write code here
        int n = prices.length;
        //dp[i][0]dp[i][0]dp[i][0]表示第i天不持股到该天为止的最大收益，dp[i][1]dp[i][1]dp[i][1]表示第i天持股，到该天为止的最大收益。
        int [][] dp = new int[n+1][2];
        // 第一天不持股
        dp[0][0] = 0;
        // 第一天持股
        dp[0][1] = -prices[0];
        for(int i=1;i < prices.length;i++){
    
            // 1、前面若干天卖掉，总收益和前一天相同
            // 2、 当天卖掉，总收益为上一天的加上卖掉的
            dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
            // 当天持股:1、还没卖 2、当天买入
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0]-prices[i]);
        }
        // 最后一天不持股
        return dp[prices.length-1][0];  
    }

20、买卖股票的最好时机(三)

题目描述：假设你有一个数组prices，长度为n，其中prices[i]是某只股票在第i天的价格，请根据这个价格数组，返回买卖股票能获得的最大收益

1. 你最多可以对该股票有两笔交易操作，一笔交易代表着一次买入与一次卖出，但是再次购买前必须卖出之前的股票
2. 如果不能获取收益，请返回0
3. 假设买入卖出均无手续费

示例：
输入：[8,9,3,5,1,3]
返回值：4
说明：第三天(股票价格=3)买进，第四天(股票价格=5)卖出，收益为2
第五天(股票价格=1)买进，第六天(股票价格=3)卖出，收益为2 总收益为4。

区别：指定最多交易操作数为两次

动态规划

思路：这道题与买卖股票的最好时机（一）的区别在于最多可以买入卖出2次，那实际上相当于它的状态多了几个，对于每天有到此为止的最大收益和持股情况两个状态，持股情况有了5种变化，我们用：
dp[i][0]表示到第i天为止没有买过股票的最大收益
dp[i][1]表示到第i天为止买过一次股票还没有卖出的最大收益
dp[i][2]表示到第i天为止买过一次也卖出过一次股票的最大收益
dp[i][3]表示到第i天为止买过两次只卖出过一次股票的最大收益
dp[i][4]表示到第i天为止买过两次同时也卖出过两次股票的最大收益

具体步骤：

• step 1：（初始状态）与上述提到的题类似，第0天有买入了和没有买两种状态：dp[0][0]=0、dp[0][1]=−prices[0]。
• step2：状态转移： 对于后续的每一天，如果当天还是状态0，则与前一天相同，没有区别；
• step3：如果当天状态为1，可能是之前买过了或者当天才第一次买入，选取较大值：dp[i】[1]=max(dp[i−1][1],dp[i−1][0]−prices[i])；
• step4：如果当天状态是2，那必须是在1的状态下（已经买入了一次）当天卖出第一次，或者早在之前就卖出只是还没买入第二次，选取较大值：dp[i][2]=max(dp[i−1][2],dp[i−1][1]+prices[i])；
• step5：如果当天状态是3，那必须是在2的状态下（已经卖出了第一次）当天买入了第二次，或者早在之前就买入了第二次，只是还没卖出，选取较大值：dp[i][3]=max(dp[i−1][3],dp[i−1][2]−prices[i]);
• step6：如果当天是状态4，那必须是在3的状态下（已经买入了第二次）当天再卖出第二次，或者早在之前就卖出了第二次，选取较大值：dp[i][4]=max(dp[i−1][4],dp[i−1][3]+prices[i])。
• step 7：最后我们还要从0、第一次卖出、第二次卖出中选取最大值，因为有可能没有收益，也有可能只交易一次收益最大。

 public int maxProfit (int[] prices) {
    
        // 动态规划
        int n = prices.length;
        int [][] dp = new int[n+1][5];
        Arrays.fill(dp[0],-10000);
        // 初始状态，没有买入
        dp[0][0] = 0;
        // 初始买入状态
        dp[0][1] = -prices[0];
        for(int i=1;i < n;i++){
    
            dp[i][0] = dp[i-1][0];
            // 状态为1
            dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);
            // 状态为2
            dp[i][2] = Math.max(dp[i-1][1]+ prices[i], dp[i-1][2]);
            // 状态为3
            dp[i][3] = Math.max(dp[i-1][3], dp[i-1][2] - prices[i]);
            // 状态为4
            dp[i][4] = Math.max(dp[i-1][4], dp[i-1][3]+ prices[i]);
        }
        return Math.max(dp[n-1][2], Math.max(0,dp[n-1][4]));
    }
}

正反遍历

题目明确指出最多可以进行两次交易，且这两次交易在时间上是有先后次序的（最多可以同时持有一只股票）；

首先假设在进行两次交易时，所获收益最大，假设第一次交易为A，第二次交易为B；即交易A发生在交易B之前；

此时我们知道A与B之间在时间上必然是没有重叠部分的（当天卖出当天买入算作没有重叠），假设A发生在第1_{i天，那么B必然发生在第i}n天（忽略当天买入天卖出的情况）；

所以便能够得出如下的公式：
$$\max \text{ Profit }=\max \{f(1,i)+f(i,n)\}$$
依据上述公式，首先进行反向遍历找出从第i天到第n天最大利润，使用一维数组做记录（第二次交易）；

接着进行正向遍历，找出最大利润（正向和反向的遍历顺序不是固定的，可以切换）。

观察下图栗子，你会发现对于只进行一次交易，当天买入当天卖出以及不进行交易的情况均满足上述公式：

public int maxProfit (int[] prices) {
    
        // 正反遍历
        int res = 0;
      // 数组中只有一个元素或为空，返回0
      if (prices.length < 2){
    
          return res;
      }
      // 首先找出第二次交易能够获得的最大利润
      // secondProfits[i]表示从第i-1天开始到
      // 结尾的一次交易能够获得的最大利润
      int[] secondProfits = new int[prices.length];
      int len = prices.length-1;
      // 最大价格
      int max = prices[len];
      // 从后往前遍历，最后一天买入卖出的利润为0
      for(int i = len - 1;i >= 0;--i){
    
          // 更新股票最大值
          max = Math.max(max,prices[i]);
          // 计算从第i-1天到结尾的最大利润
          secondProfits[i] = Math.max(secondProfits[i+1],
                                      max - prices[i]);
      }
      // 从前往后遍历时的股票价格最小值
      int min = Integer.MAX_VALUE;
      for (int i = 0;i < len;++i){
    
          // 更新最低股票价格
          min = Math.min(min,prices[i]);
          // 找出两次交易最大利润的组合
          res = Math.max(res,prices[i] -
                         min + secondProfits[i+1]);
      }
      return res;
    }