[普通物理] 半波损失 等厚与等倾干涉

1.半波损失

记住个结论

由疏到密，看反射，半波损失，相位变
意思就是从折射率小的介质向折射率大的介质，并且还是反射的话，那么便会存在半波损失

折射不发生半波损失
由密到疏，即使是反射也不存在半波损失

在做题的过程中，常常出现的是，垂直入射：

2 等倾干涉

其实半波损失里面提及的例子便是等倾干涉，也就是光程差是由入射角决定的

对于厚度均匀的薄膜，光程差是由入射角决定的，凡是以相同倾角入射的光，经膜的上、下表面反射后产生的相干光束都有着相同的光程差，从而对应着干涉图样中的一条条纹，故将此类干涉条纹称为等倾干涉。

3 等厚干涉

对于等厚干涉，意味着光程差与其厚度d的取值有关

3.1 空气劈尖

事实上，由于细发丝直径及其小，因此入射角i几乎可以看作是0，那么三层介质分别为玻璃-空气-玻璃，很明显最后的光程差会有附加光程差又由于入射可以看成垂直入射，那么明纹暗纹可以表示为：

2.2 牛顿环

至于牛顿环，其实就是多个劈尖而已，没什么好说的。

知道牛顿环就是多个劈尖组成，那么就很容易，解释牛顿环为什么里面是稀疏，外面是密集了，里面的劈尖角度小，所以稀疏，外面的角度大，相对密集，并且牛顿环的中心依然是暗条纹。

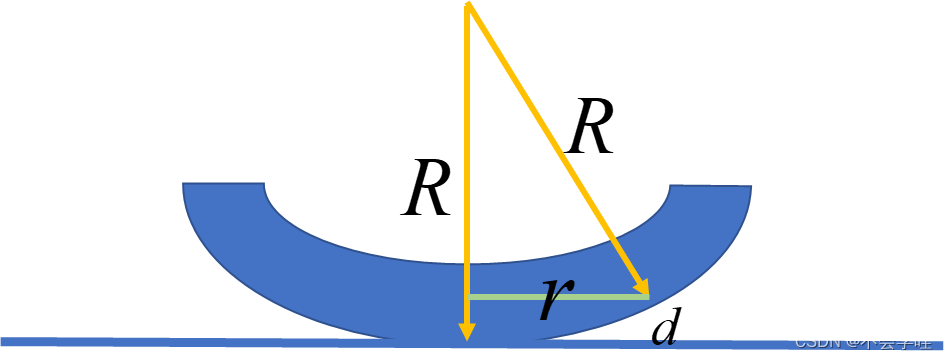
题目有时会考这个明暗干涉条纹与距离牛顿环中心的距离r之间的关系。推一下：