MIP nerf: anti aliasing multiscale neural radiation field iccv2021

Aliasing phenomenon

Data collection , If the sampling frequency does not satisfy the Nyquist sampling theorem , It may cause aliasing of sampled signals .

When the sampling frequency setting is unreasonable , That is, the sampling frequency is lower than 2 Times the signal frequency , It will cause the original high-frequency signal to be sampled into a low-frequency signal . As shown in the figure below , The red signal is the original high frequency signal , However, the sampling frequency does not meet the requirements of the sampling theorem , The actual sampling points are shown as blue solid points in the figure , Connect these blue actual sampling points into a curve , It is obvious that this is a low frequency signal .

Equal time sampling of continuous signals , If the sampling frequency does not satisfy the sampling theorem , The sampled signal frequency will be aliased , That is, high-frequency signals are mixed into low-frequency signals .

For the image , The high-frequency information of the image is the part with steep gray change , The aliasing part of the image, that is, the high-frequency content, is represented as the low-frequency content , That is what we call fuzzy phenomenon （ Close observation ）, And jagged edge appearance （ Long distance observation ）.

NeRF Excellent results can be generated only when the distance between the camera and the object is fixed , When the camera zooms in , Blurring and jagging occur when you zoom out of the scene . The reason is that the sampling frequency is lower than the frequency of the real original signal , To solve this problem , We can ： Improve sampling rate or roughly remove high-frequency components （ Use low-pass filter to smooth the edge ）.

• NeRF（ Left ） There are short-range blur and long-range aliasing ,Mip-NeRF（ Right ）

NeRF Only one light is emitted for each pixel , If you emit multiple rays , Improved sampling rate , To some extent, it can solve the problems of blur and aliasing , But this method greatly increases the amount of calculation , Efficiency is too low , So ,mip-nerf A scheme of using cone to replace light is proposed .

Mip-NeRF summary

mip From Latin （ A small space for many things ）, In computer graphics ,mipmapping Is a kind of accelerated rendering , Techniques for reducing image aliasing . In short ,mipmapping The main picture is reduced to a series of pictures which are reduced in turn , And save these smaller images with lower resolution . This strategy is called pre-filtering, The computational burden of anti aliasing is concentrated on Preprocessing ： No matter what needs to be done later on texture How many times to render , Only the first preprocessing is needed .

Mip-NeRF The background is ： During rendering , If NeRF At every pixel use single ray Come on sample scene ,（NeRF When rendering ） There will be blurring （blurred） And serrations （aliased） The situation of , This is usually due to the resolution of multiple pictures corresponding to the same scene （resolution） Caused by inconsistency （ Due to different camera distances , Cause the relative sampling frequency to change , Thus causing signal distortion ）. The simplest solution is rendering time , For each pixel use multiple rays. But yes. NeRF It's not realistic , Because along a ray Rendering requires query One MLP Hundreds of times .

Mip-NeRF Solutions and NeRF There is an essential difference ：NeRF Rendering is based on ray Of , However Mip-NeRF Is based on conical frustums（ Cone ） Of , And is anti-aliased（ Anti aliasing ） Of . Final ,Mip-NeRF And NeRF Faster than having 、 smaller 、 More accurate advantages , More suitable for handling multiscale The data of .

Location code IPE

Classic location coding （ be used for Transformer And neural radiation fields ） Map a single point in space to a feature vector , Each element in the vector is generated by a sine curve with exponentially increasing frequency ：$${\gamma }_w(x)=sin(wx),\gamma (x)=[{\gamma }_{2^l}(x){]}_{l=0}^{L-1}$$ here , We show how these eigenvectors change with the movement of points in one-dimensional space （ Make $L=5$）：

mip-nerf Of integrated positional encoding Consider... In space Gaussian regions, Not a point of infinity . This provides a natural way , You can put the space “region” As query Input to is based on coordinate The neural network of . The expected value of each location code has a simple form ：$$E_{x\sim N(\mu ,{\sigma }^2)}[{\gamma }_w(x)]=sin(w\mu )exp(-(w\sigma {)}^2/2)$$ We can see , When considering broader region when （ vision ）, High frequency information will automatically shrink to zero , So as to provide more low-frequency information for the network . With region narrow （ Close up ）, These position characteristic signals will be close to the classical position coding .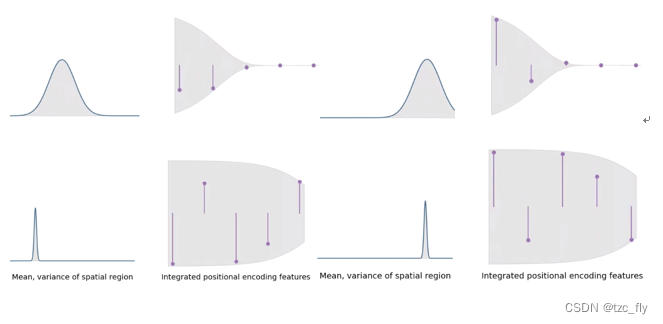

This dynamic setting , bring nerf Process the vision and automatically filter the high-frequency information , The sawtooth phenomenon is relieved （ That is, remove the high-frequency components in the scene ）, Recover the processing of high-frequency information when processing close range .

Mip-NeRF

Use IPE To train NeRF To generate antialiasing rendering .mip-nerf Instead of casting an infinitely wide ray per pixel , Instead, it projects a complete 3D Cone . For each query point along the ray , We consider its associated cone truncated cone . The same point in the observation space of two cameras at different positions may produce different conical truncated cones , As shown in the figure below ：

We fit multivariate Gauss to a conical truncated cone , And use the above IPE establish MLP The input eigenvector of the network .

Intuitive to see , The advantage of using cone rendering is ： The cone reflects the shape and size of a point in the scene , Because from different perspectives , The shape and size of a point are different , That is, conical truncated cone （ Trapezoid in the picture above ） The size and shape of . Reflected in the calculation is the camera in different positions , The expected values of position codes for the same observation point are different .

Introduction

Neural radiation fields （NeRF） Has become a compelling strategy , Used to learn representation from images 3D Objects and scenes , To render a new view with photorealistic realism . Even though NeRF And its variants have achieved impressive results in a series of view composition tasks , but NeRF The rendering model is flawed , May cause excessive blurring （ Close up ） And serrations （ vision ）.NeRF The traditional discrete sampling is replaced by a continuous volume function , It is parameterized as a multilayer perceptron （MLP）, The perceptron inputs from the 5D coordinate （3D Location and 2D Look in the direction ） Scene attributes mapped to this location （ Bulk density and emissivity determined by viewing angle ）. To render the color of a pixel ,NeRF A ray will be cast through this pixel , And output it to its volume representation , Sample queries along this ray MLP Get scene properties , Combine these values into a single color .

Although when all training and test images only observe the scene content from a roughly constant distance , This method works well （ As in the NeRF And most of the follow-up work ）, but NeRF Rendering shows obvious flaws in less artificial scenes . When the training image observes the scene content at multiple resolutions , Recovered NeRF Rendering in close-up view （ Observe the situation closely ） Is too vague , In the far view （ Long distance observation ） Contains jagged . A simple solution is to adopt the strategy used in offline ray tracing ： Oversampling each pixel by pushing multiple rays into their footsteps . But for the neural volume representation （ Such as NeRF） Come on , This method is expensive , Because rendering a ray requires querying MLP Hundreds of times , It will eventually take several hours to reconstruct a scene .

In this paper , We start with the... Used to prevent aliasing in the computer graphics rendering pipeline mipmapping Method .mipmap In fact, it is a multi-resolution image pyramid structure .

Our solution is called mip-NeRF（multum in parvo-NeRF, Such as “mipmap”）.mip-NeRF The input is one Three dimensional Gaussian distribution , Is the integral of the radiation field region. Pictured 1 Shown , And then we can query by every distance along the cone mip-NeRF, The pixel is rendered using a Gaussian distribution approximating the cone section corresponding to the pixel . In order to 3D Location and its surroundings Gaussian region Encoding , We propose a new feature representation ： Integrated position coding （IPE,integrated positional encoding）. This is a NeRF The location code of （PE） Promotion of , It allows space region Characterized compactly , Not a single point in space .

• chart 1：NeRF(a) Point to point along the ray traced through the pixel from the camera projection center $\text{x}$ sampling ,$\text{d}$ Is the direction of observation , Then use position coding PE $\gamma$ Code these points , To generate features $\gamma (\text{x})$.Mip-NeRF(b) Instead, it is interpreted as a three-dimensional conical frustum defined for camera pixels . then , Use our integrated location code （IPE） These conical truncated cones are characterized ,IPE Its working principle is to use multivariate Gauss approximation to truncate cone , Then calculate the integral on the Gauss coordinate position coding $E[\gamma (\text{x})]$.

Mip-NeRF Greatly improved NeRF The accuracy of the . On a challenging multi-resolution benchmark proposed by us ,mip-NeRF be relative to NeRF Can reduce on average 60% Error rate .Mip-NeRF The scale aware structure of also allows us to NeRF For layered sampling "coarse" and "fine"MLP Merge into a single MLP in . therefore ,mip-NeRF Slightly faster than NeRF, And it has half the parameters .

Method

When replacing rays with cones , Sampling is no longer a discrete set of points , But a continuous conical cutting platform （conical frustum）, This can solve NeRF The problem of the volume and size of the light observation range is ignored .

In order to simplify the calculation , We use 3D Gaussian To approximate conical frustum（ Conical frustum ）, And propose to use IPE Instead of PE.IPE Defined as Gaussian distribution positional encoding The expectation of .

Gaussian There are many advantages of distribution , One of them is linear transformation . take positional encoding Rewritten in matrix form , Input Gaussian distribution for operation , It is equivalent to transforming the mean and covariance of Gaussian distribution .

First ,PE The matrix form of is ：

Be careful ,$\text{x}$ It's spatial location ,$\text{d}$ Is the direction of observation , We define ${\mu }_t$ Is the sampling point $t$ The average distance from the corresponding cone section to the camera （ The average distance along the light ）, in addition ,${\sigma }_t^2$ Is the variance of the distance along the ray ,${\sigma }_r^2$ Is the variance of the distance perpendicular to the light .

We can get the sampling point $t$ Gaussian distribution of the corresponding cone section ：$$\text{u}=\text{o}+{\mu }_t\text{d}$$$$\Sigma ={\sigma }_t^2(\text{d}{\text{d}}^T)+{\sigma }_r^2(\text{I}-\frac{\text{d}{\text{d}}^T}{||\text{d}|{|}_2^2})$$ We encode the position of Gaussian distribution , The position coding must obey Gaussian distribution , And the mean and variance are ：$${\text{u}}_{\gamma }=\text{P}\text{u}$$$${\Sigma }_{\gamma }=\text{P}\Sigma {\text{P}}^T$$ According to this Gaussian distribution , We can get IPE：$$\gamma (\text{u},\Sigma )=E_{\text{x}\sim N({\text{u}}_{\gamma },{\Sigma }_{\gamma })}[\gamma (\text{x})]$$$$=[\text{sin}({\text{u}}_{\gamma })\circ exp(-(\frac{1}{2})diag({\Sigma }_{\gamma })),\text{cos}({\text{u}}_{\gamma })\circ exp(-(\frac{1}{2})diag({\Sigma }_{\gamma })){]}^T$$$$diag({\Sigma }_{\gamma })=[diag(\Sigma ),4diag(\Sigma ),...,4^{L-1}diag(\Sigma ){]}^T$$ among ,$\circ$ by element-wise The product of .$diag$ Is the diagonal of the matrix .mip-nerf Sampling with truncated cones , Information of different scales is considered , So just learn one MLP Can represent coarse-grained and fine-grained information .

Discuss

• chart 2：NeRF Location code used PE（ Left ） and mip-nerf Integrated position coding IPE（ Right ）. because NeRF Sample along each ray , And encode all frequencies , For those high frequency features （ Sampling frequency exceeded ） It will always cause the rendering to be aliased . By integrating... On each bay PE features , When the sampling frequency period is the same as IPE The interval size of is smaller than that of ,IPE The high frequency dimension of the feature shrinks to zero , Avoid aliasing .

The figure above visualizes IPE and PE The difference between one-dimensional features of .IPE The behavior of features is intuitive ： If the frequency period in the position coding is less than the construction IPE Interval width of the feature （ under these circumstances , On this interval PE The oscillation will be repeated ）, Then the characteristic at this frequency will be reduced to 0.IPE Feature is an effective anti aliasing location coding , The size and shape of the space volume can be gently encoded .

---

IPE Each sampling can ensure that it is relative to IPE The high frequency feature of feature interval is weakened , Because the Gaussian distribution of each cone always follows IPE The characteristic interval changes dynamically

---

Mip-NeRF The main contribution is to improve the sampling method , Use a cone instead of a point in the light , For the sake of calculation , A three-dimensional Gaussian distribution is proposed region Approximate conical truncated cone , According to the characteristics of Gaussian distribution , Get the Gaussian distribution corresponding to the position coding , Sampling position coding from this Gaussian distribution , And calculate the expected position code as the last .

The position coding which obeys Gauss distribution can automatically when the sampling frequency is low （IPE When the feature interval is wide ） Weakening high frequency features , So as to alleviate the aliasing phenomenon . This sampling design itself determines that it is suitable for multi-scale situations , therefore ,Nerf Of the two MLP Can be combined into one MLP.