Time series analysis - how to use unit root test (ADF) correctly?

1、 effect

When using many time series models , Such as ARMA、ARIMA, Will require the time series to be stable , So when studying a time series , The first step is to test the stability , In addition to the method of visual inspection , In addition, the more commonly used strict statistical test method is ADF test , Also called unit root test . Unit root test refers to checking whether there is a unit root in the sequence , Because there is a unit root, it is a nonstationary time series .

2、 Input / output description

Input ：１ Quantitative variables of time series data
Output ： The sequence data is stable in several order difference

3、 Learning Websites

SPSSPRO- Free professional online data analysis platform

4、 Case example

Case study ： Based on a magazine 1995-2019 Annual printing volume data , Judge whether it is stable .

5、 Case data

Unit root test （ADF） Case data

6、 Case operation

Step1： New analysis ;
Step2： Upload data ;
Step3： Select the corresponding data to open and preview , Click start analysis after confirmation ;

step4： choice 【 Unit root test （ADF)】;
step5： View the corresponding data format ,【 Unit root test （ADF)】 Request input １ Quantitative variables of time series data .
step6： Click on 【 To analyze 】, Complete the operation .

7、 Output result analysis

Output results 1：ADF Check list

*p<0.05,**p<0.01,***p<0.001
Chart description ： The above table is ADF The results of the test , The results of this sequence test show that , Based on field print quantity （ ten thousand ）: The difference is 1 Step time , Significance P The value is 0.000***, The level is significant , Rejection of null hypothesis , This series is a stationary time series . And in the original sequence and the difference is 2 Step time , Significance P Greater than 0.05, The original hypothesis cannot be rejected , Explain the original sequence and the difference 2 The order sequence is nonstationary .

Output results 2： Original sequence diagram

Chart description ： The figure above shows the original figure without difference . among X The axis represents the time item （ year ）,Y The axis represents the value （ Magazine print volume ）, Subjectively , The original sequence diagram has an increasing trend , Is a nonstationary sequence .ADF The unit root test also shows that the first-order difference sequence is non-stationary .

Output results 3： First order difference graph

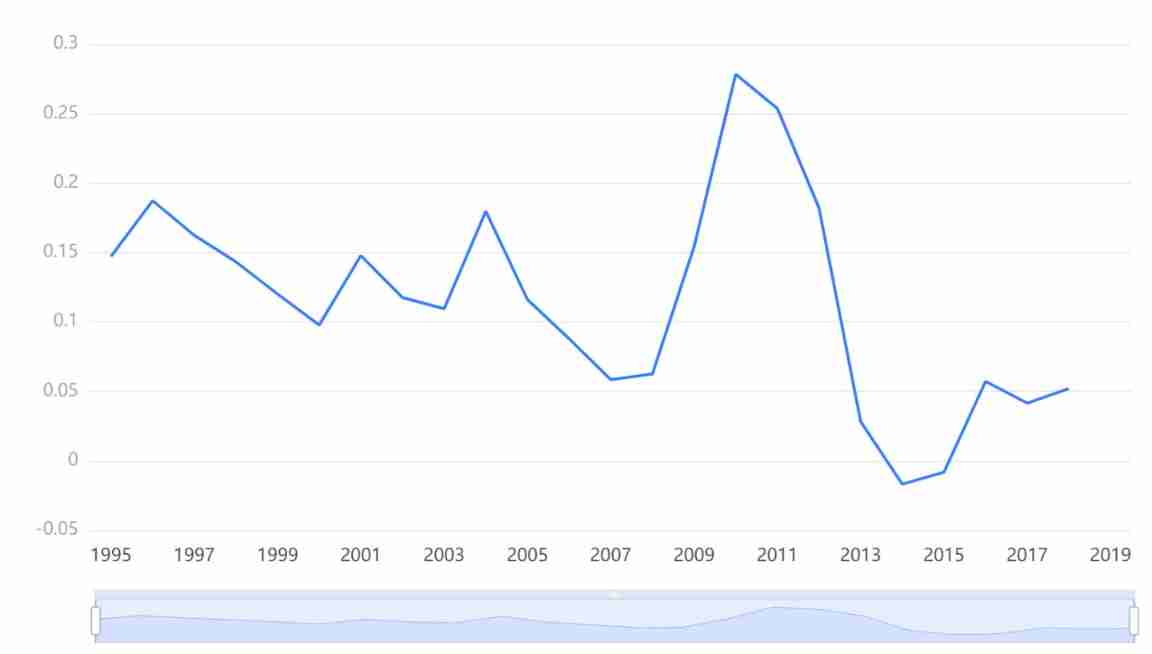
Chart description ： The figure above shows the result of the first-order difference . When the time intervals are equal , Use the next value , Subtract the previous value , Get the first-order difference . Subjectively , The first-order difference sequence is numerically 1.5 Up and down , There is no obvious increasing and decreasing trend , It is preliminarily judged that the first-order difference sequence is a stationary sequence .ADF The unit root test also shows that the first-order difference sequence is stationary .

Output results 4： Second order difference graph

Chart description ： The figure above shows the result of the second-order difference . Do the same action twice , That is, on the basis of the first-order difference, the latter value is subtracted by another value , Call “ Second order difference ”. For the stationary test of the second order difference sequence , adopt ADF The unit root test is used to obtain the non-stationary second-order difference sequence .

8、 matters needing attention

• Enter the time item of the page [ The nominal ] Variables are only rendered for drawing X For axis coordinates , No other meaning .

9、 Model theory

To any one AR（p) The process

His characteristic equation is ：

If all the characteristic roots of the equation lie in the unit circle of , namely

Then the sequence is stable .
If there is a unit root , Then the sequence is nonstationary , And the sum of the regression coefficients is exactly equal to 1

10、 reference

[1] Wang Yan ． Using time series analysis [M]． Beijing ： Renmin University Press of China 2005．