当前位置:网站首页>高数 | 精通中值定理 解题套路汇总
高数 | 精通中值定理 解题套路汇总
2022-06-24 22:58:00 【西皮呦】
解题套路汇总
套路一


![]()

![]()


注:柯西中值定理中的 g‘(x)≠0 同时限制了两个分母 可以用反证法+罗尔

![]()







![]()




![]()

罗尔定理得到的根一定是单根。

套路二 辅助多项式
【注】构造
的目的,主要是将题干中的那些“参差不齐”的函数值和导数值全部“归零”,从而使得
能够不断使用罗尔定理,大大简化了问题!
【注】设函数时,若已知零点,举例,比如二次函数:设为




【注】回顾辅助多项式的解题过程可知,由于
是n次多项式,而我们最后还是对辅助函数
连续求了n次导,从而得到了
,所以真正影响、决定最终结论的,只有
中的最高次项的系数!而至于那些低次项都在一次次的求导过程中消失殆尽了。
(当然,这不代表那些低次项的系数可以随便乱写,因为只有
中的每一个系数都准确无误时,
才可能出现那么多的零点和驻点,才可能满足罗尔定理的使用条件,你不能因为那些低次项的系数不影响
,你就认为他们毫无作用,工具人也是人~)





【注】特别注意的是,本题中
和
虽然有相同的最小值
,但它们取到最小值的横坐标却不一定相同。故需要分类讨论。该思想可以应用到2007年的考研大题中!


【注】
前文中已经提过,在使用辅助多项式解题时,若预证结论为
,则需要构造一个
次多项式进行拟合。由于n次多项式中有
个系数,所以题干中只有
个独立条件时,则无法顺利解出辅助函数中所有系数。
为了解决这个问题,我们需要给
“强行附加约束条件”,使得构造出的
能够顺利解出题目。
至于需要附加一个什么样的条件,则需要“具体问题具体分析”,不能一概而论,但核心原则是“缺什么补什么”。




补充例题:

【解答】
见到题目给出三个点我们很容易想到罗尔定理

却发现这三个点不相等,那么我们会立马想到泰勒定理

但在考研数学中不能直接使用导数介值定理(这里注意本题的题干[没给连续]),所以我们可以想到什么来规避它呢?
构造辅助多项式:


【真题】


套路三 公式法(积分因子法)
【注意】
1、公式中的
不需要加任意常数
,因为我们只需要找到一个辅助函数就够了。
2、
不一定恰好就是欲证结论,有时需要再变形一下才行,但一定要注意——对
变形时,如果等式两边同时约去某个东西,或者同除某个东西,需要考虑它是否为0.




需要分类讨论:
①
如果ξ≠0,则在F'(ξ)=0两边约去ξ,得到欲证结论;
②
如果ξ=0,那说明0在区间(a,b)内部,即在定义域内部。
又因为F(x)=x²f(x),所以F(0)=0,而又因为F(a)=F(b)=0,所以推出F有三个零点,分别是a,0,b。
所以我们在【a,0】和【0,b】分别用罗尔定理,即可证出存在两个不为0的ξ1和ξ2,
使得F'(ξ1)=F'(ξ2)=0,此时由于ξ1和ξ2不为0,所以是可以被约去。









【注1】本题欲证结论为
,最直观的感觉就是“一阶导
哪去了?”。所以,这种题目一般都需要认为引入一阶导
,达到一个降阶的效果。
【注2】本题在欲证等式两边同时减去
,其实也可以,本质是一样的。
【注3】若欲证结论中已经含有
,则不需要再人为引入
了,但有时需要将一阶导
合理分配,使他们达到一种“平衡”。
合理分配,达到平衡

 【注】将用这道题为例给大家展示为什么在马克总主义哲学中,会强调“真理与语误可以相互转化”,也隐藏着以后会显露出来的真理的成分或萌芽。
【注】将用这道题为例给大家展示为什么在马克总主义哲学中,会强调“真理与语误可以相互转化”,也隐藏着以后会显露出来的真理的成分或萌芽。


其实错误的解法是由内而外拉格朗日。正确的解法是由外而内拉格朗日。
套路四 具体问题具体分析

虽然前面已经讲过公式法,但公式也并不是万能的,此类题我们需要观紧式子结构,去分析你要证明的结论是哪个函数求导以后的样子,然后尝试将其还原。
总之,还原出辅助函数 的过程是朝着熵减的方向前进,所以有困难是正常的!
的过程是朝着熵减的方向前进,所以有困难是正常的!









【注】本题应说明,分母为何不为0。








伪双中值问题!


















套路五 分离常数和中值,直接拉或柯西





此题为上一专题 套路四的例2







套路六 双中值定理【虚假的双中值】


【注】以此题为例,总结出一套组合拳,通杀——
- ① 将复杂的中值分离出来
- ② 将其还原
- ③ 恒等变形或带入条件
- ④ 再用一次中值定理或柯西
- ⑤ 战斗结束
【三中值例题】








套路七 【真正的双中值定理】





【n中值问题】




【例4:三个中值也可以取自两个区间】


【补充】这些不同的中值不一定来源于不同的区间,也有可能是一个来源于开区间内部,而另外一个来源于区间端点,这类题目很有意思,比如下面这道类题。
【类题前 铺垫一下~ 不然可能不会挖掘题目条件】



套路八 求中值θ的极限

套路 四部曲:重新展开,对比两式、建立等式,分离中值θ,求极限。



【注】没展干净,等式两边不能同除。







【例4 下面这道题,虽然也是计算  的极限,但是由于
的极限,但是由于 的表达式已知,所以我们可以轻松地从题干中反解出
的表达式已知,所以我们可以轻松地从题干中反解出  的表达式,毫无难度】
的表达式,毫无难度】

【错误解法】



【正确解法】

套路九 泰勒中值定理
若欲证结论中含有高阶导(二阶导以上):一般可以采用“带拉格朗日余项的泰勒展开”进行证明。再具体操作中,最重要的是恰当的 选取展开点 和 被展开点
和 被展开点 的位置。
的位置。
一般而言,选取导数信息多的点作为展开点,选取只告诉函数值的点作为被展开点。
- 套路:
- 有限区间:在端点展开,或在中点展开
- 无限区间:在任意点展开
注意:




【注】
本题需要用到 连续函数 介值定理的一个推论:
其中
,或
由于“导函数天生满足介值定理”,故条件中的“三阶导数连续”可以改为“三阶可导”!!
【例2 :极值点蕴含了导数的信息,所以常常将函数在极值点处展开】



注:

接下来的两道题,题干条件均未告知经历点处的函数值和导数值,所以也只有根据结论来猜测展开点和被展开点该如何选取。

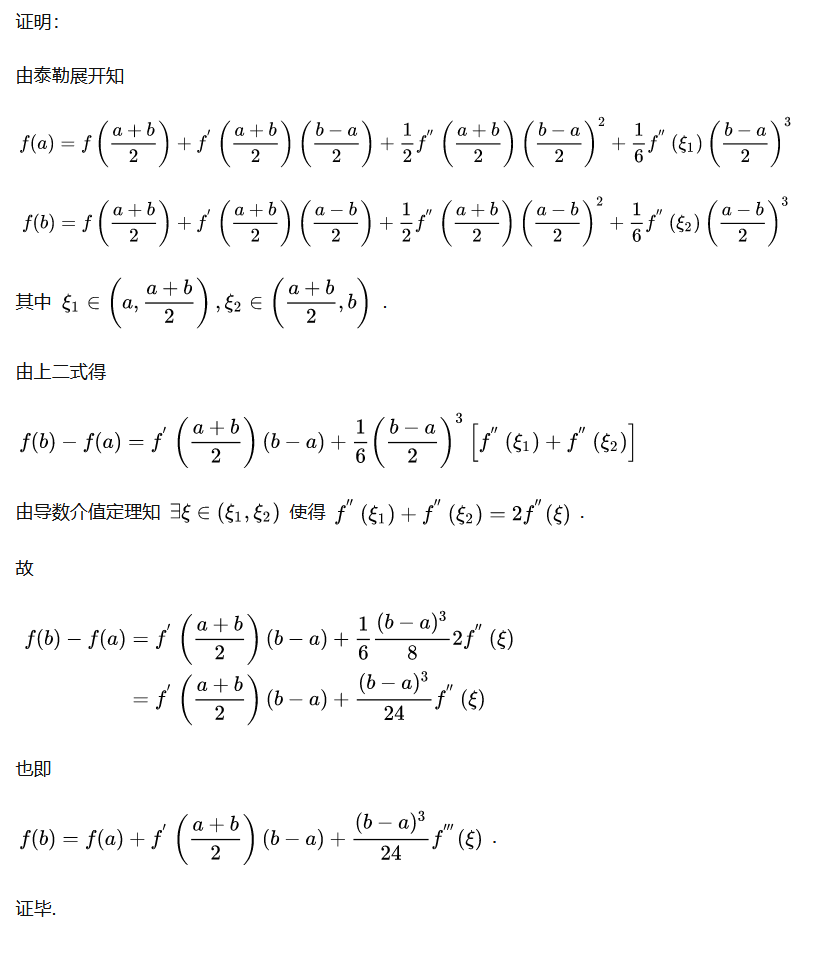



经验:在 “中间点”展开

例4:在一条笔直的道路上,一辆汽车从开始启动到刹车停止,共用了单位时间走完了单位路程.。证明:至少有一个时刻,其加速度的绝对值不少与 4。


【注】对于这种 “两个端点的函数值,导数值均已知” 的题,为了充分利用已知条件,初学者可能会选择两端点处相互展开,但这样误差会很大(因为泰勒展开本身就是估计,它要求展开点与被展开点的距离不需太大),所以采用中点在端点处展开。
利用上面的注意事项,便可轻松秒杀下面这道题。



【注】泰勒+任一点处展开。


开始无穷区间咯 ~



资料来自 考研竞赛凯哥 ~
泰勒中值定理,看这个视频,足够了!!!_哔哩哔哩_bilibili
自用 整理~
题目源自(谢谢学长~
边栏推荐
- mysql命令备份
- F - spices (linear basis)
- 常用的软件测试工具清单,请查收。
- Are programmers from Huawei, Alibaba and other large manufacturers really easy to find?
- 记一次beego通过go get命令后找不到bee.exe的坑
- EasyCVR平台EHOME协议接入,视频播放出现断流是什么原因?
- Exploring the mystery of C language program -- C language program compilation and preprocessing
- 算力服务网络:一场多元融合的系统革命
- Viewing MySQL password on Linux_ MySQL forgets password "suggestions collection" under Linux
- 背了八股文,六月赢麻了……
猜你喜欢

Use of hashcat

保险APP适老化服务评测分析2022第06期

元宇宙的生态圈

Folding screen will become an important weapon for domestic mobile phones to share the apple market

如何通过EasyCVR接口监测日志观察平台拉流情况?

常用的软件测试工具清单,请查收。

都2022年了,你还不了解什么是性能测试?

How to quickly familiarize yourself with the code when you join a new company?

EasyCVR国标协议接入的通道,在线通道部分播放异常是什么原因?

The ecosystem of the yuan universe
随机推荐
MOS管相关知识
vim的Dirvish中文文档
What is the reason for the disconnection of video playback due to the EHOME protocol access of easycvr platform?
【STL源码剖析】STL六大组件功能与运用(目录)
Hashcat 的使用
把 Oracle 数据库从 Windows 系统迁移到 Linux Oracle Rac 集群环境(3)—— 把数据库设置为归档模式
After reciting the eight part essay, I won the hemp in June
Intranet learning notes (7)
Once beego failed to find bee after passing the go get command Exe's pit
会自动化—10K,能做自动化—20K,你搞懂自动化测试没有?
Kaggle 专利匹配比赛赛后总结
AI服装生成,帮你完成服装设计的最后一步
Android Internet of things application development (smart Park) - set sensor threshold dialog interface
测试/开发程序员,30而立,你是否觉得迷茫?又当何去何从......
常用的软件测试工具清单,请查收。
Dirvish Chinese document of vim
Uncaught Error: [About] is not a <Route> component. All component children of <Routes> must be a <Ro
产业互联网的概念里有「互联网」字眼,但却是一个和互联网并不关联的存在
如何选择正规安全的外汇交易平台?
Convert string array to list collection



 的目的,主要是将题干中的那些“参差不齐”的函数值和导数值全部“归零”,从而使得
的目的,主要是将题干中的那些“参差不齐”的函数值和导数值全部“归零”,从而使得

 是n次多项式,而我们最后还是对辅助函数
是n次多项式,而我们最后还是对辅助函数 连续求了n次导,从而得到了
连续求了n次导,从而得到了 ,
, ,
, ,则需要构造一个
,则需要构造一个 次多项式进行拟合。由于n次多项式中有
次多项式进行拟合。由于n次多项式中有 个系数,所以题干中
个系数,所以题干中
 不需要加任意常数
不需要加任意常数 ,因为我们只需要找到一个辅助函数就够了。
,因为我们只需要找到一个辅助函数就够了。 不一定恰好就是欲证结论,有时需要再变形一下才行,但一定要注意——对
不一定恰好就是欲证结论,有时需要再变形一下才行,但一定要注意——对 ,最直观的感觉就是“一阶导
,最直观的感觉就是“一阶导 哪去了?”。所以,这种题目一般都需要认为引入一阶导
哪去了?”。所以,这种题目一般都需要认为引入一阶导 ,其实也可以,本质是一样的。
,其实也可以,本质是一样的。 ,则不需要再人为引入
,则不需要再人为引入

![\xi\in [x_{1},x{_2}]](http://img.inotgo.com/imagesLocal/202206/25/202206242258097597_71.gif) ,或
,或![\xi\in [x_{2},x{_1}]](http://img.inotgo.com/imagesLocal/202206/25/202206242258097597_10.gif)