当前位置:网站首页>Distance measure - cosine distance
Distance measure - cosine distance
2022-06-23 04:40:00 【Fanyi】
Python Learning Series : Catalog

One 、 summary
Trigonometric functions , I believe everyone has learned in junior high school , And what we're talking about here Cosine distance (Cosine Distance) The calculation formula is similar to that learned in high school .
In Geometry , The cosine of the included angle can be used to measure two directions ( vector ) The difference of ; So it can be extended to machine learning , To measure the difference between sample vectors .
therefore , Our formula has to be changed slightly , So that it can be expressed as a vector .
Two 、 Calculation formula
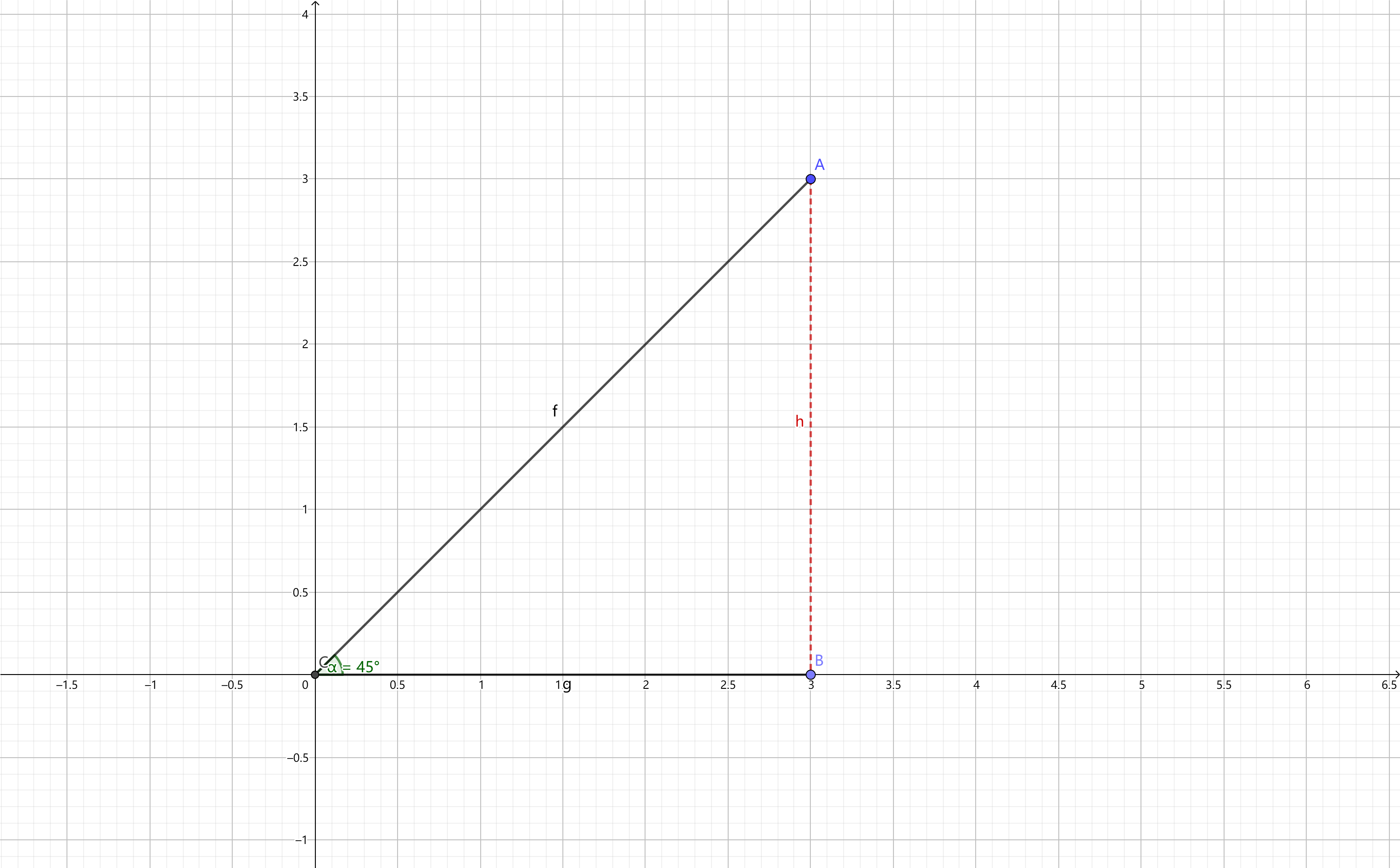
① Cosine distance in two-dimensional plane
hypothesis Two dimensional plane There are two vectors inside : A ( x 1 , y 1 ) A(x_{1},y_{1}) A(x1,y1) And B ( x 2 , y 2 ) B(x_{2},y_{2}) B(x2,y2)
Then the A A A、 B B B The cosine distance formula of two vectors is :
c o s ( θ ) = a ⋅ b ∣ a ∣ ∣ b ∣ cos(\theta)=\frac{a\cdot b}{|a| |b|} cos(θ)=∣a∣∣b∣a⋅b
c o s ( θ ) = a ⋅ b ∣ a ∣ ∣ b ∣ = x 1 x 2 + y 1 y 2 x 1 2 + y 1 2 x 2 2 + y 2 2 \begin{aligned} cos(\theta)&=\frac{a\cdot b}{|a| |b|}\\ &=\frac{x_{1}x_{2}+y_{1}y_{2}}{\sqrt{x_{1}^2+y_{1}^2}\sqrt{x_{2}^2+y_{2}^2}} \end{aligned} cos(θ)=∣a∣∣b∣a⋅b=x12+y12x22+y22x1x2+y1y2
② n Cosine distance in dimensional space
Generalized to n Two vectors of dimensional space A ( x 11 , x 12 , . . . , x 1 n ) A(x_{11},x_{12},...,x_{1n}) A(x11,x12,...,x1n) And B ( x 21 , x 22 , . . . , x 2 n ) B(x_{21},x_{22},...,x_{2n}) B(x21,x22,...,x2n), Then the cosine distance is :
c o s ( θ ) = a ⋅ b ∣ a ∣ ∣ b ∣ = ∑ k = 1 n x 1 k x 2 k ∑ k = 1 n x 1 k 2 ∑ k = 1 n x 2 k 2 \begin{aligned} cos(\theta)&=\frac{a\cdot b}{|a| |b|}\\ &=\frac{\sum_{k=1}^n x_{1k} x_{2k}}{\sqrt{\sum_{k=1}^nx_{1k}^2}\sqrt{\sum_{k=1}^nx_{2k}^2}} \end{aligned} cos(θ)=∣a∣∣b∣a⋅b=∑k=1nx1k2∑k=1nx2k2∑k=1nx1kx2k
③ Be careful
- The value range of cosine distance is [ − 1 , 1 ] [-1,1] [−1,1].
- The larger the cosine, the smaller the angle between the two vectors , The smaller the cosine, the larger the angle between the two vectors .
- When the directions of two vectors coincide, the cosine takes the maximum 1 1 1, When two vectors are in opposite directions, the cosine is the minimum − 1 -1 −1.

边栏推荐
- 制造型企业开发的SRM供应商管理系统特点是什么
- 8位全加器原理
- Pta:6-29 application of virtual base classes - people, teachers and students
- laravel 8.4 路由问题,结尾处是编辑器左侧对照表,小白可看懂
- ② cocoapods原理及 PodSpec 文件上传操作
- LabVIEW在同一表中同时显示十六进制字符和普通字符
- Pta:7-58 Book audio-visual rental management
- 距离度量 —— 余弦距离(Cosine Distance)
- [deep learning] deep learning reasoning framework tensorrt MNN openvino onnxruntime
- How to make the page number start from the specified page in word
猜你喜欢

Imitation 360 desktop suspended ball plug-in

Pytoch --- use pytoch's pre training model to realize four weather classification problems

LabVIEW displays both hexadecimal and normal characters in the same table

Halcon glue line detection - template matching, pose transformation, glue width, glue continuity detection
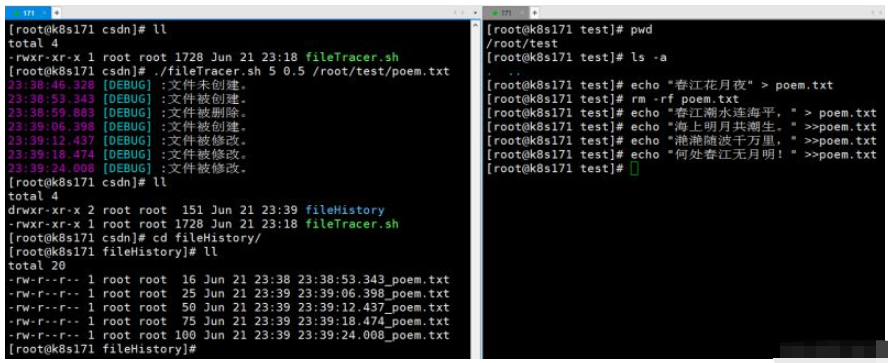
How to use shell script to monitor file changes

LabVIEW在同一表中同时显示十六进制字符和普通字符

X24cxx series EEPROM chip C language universal reading and writing program

Leetcode 1208. Try to make the strings equal as much as possible (finally solved, good night)

JVM调优简要思想及简单案例-为什么需要JVM调优?

Analysis on the current situation of the Internet of things in 2022
随机推荐
volatile 与线程的那些事
LabVIEW displays both hexadecimal and normal characters in the same table
Ms-fsrvp forced abuse of POC
Permission Operation in dynamics 365 plug-in
Volatile and threads
Kail 渗透基本素养 基础命令
PTA:7-63 计算高考状元
x24Cxx系列EEPROM芯片C语言通用读写程序
[acnoi2022] no way without guessing
Pta:6-71 clock simulation
什么是元数据
【二叉树】翻转等价二叉树
Online text filter less than specified length tool
Cool mouse following animation JS plug-ins 5
一篇文章学会er图绘制
Create a desktop shortcut to your appimage
Pta:7-63 calculate the number one in the college entrance examination
Cocos学习日记2——脚本和属性
[ACNOI2022]不猜不行
What is the open source database under Linux