当前位置:网站首页>[hdu] p1466 calculate the number of intersections of straight lines
[hdu] p1466 calculate the number of intersections of straight lines
2022-06-23 01:22:00 【Lupin123123】
Topic link
Combinatorial problems , Consider recursion
If requirement n Any two of these lines have intersections , set up a n a_n an by n The number of intersections generated by the lines , So easy to get a n = a n − 1 + n − 1 a_n=a_{n-1}+n-1 an=an−1+n−1 Because the second n A line is added to the front n-1 The plane of a straight line , Will be with this n-1 All the lines form an intersection .
Now get rid of “ Two intersect ” Conditions , that In joining the n When there is a straight line, there is a straight line parallel to it , No contribution to intersection points . This tells us Consider the problem from the perspective of parallel lines . set up f ( i , j ) f(i,j) f(i,j) To have i A straight line forms j Is the intersection feasible , front i-1 This straight line has k The bar is parallel to it , f ( i , j ) = 1 f(i,j)=1 f(i,j)=1 If and only if f ( i − 1 − k , j − ( k + 1 ) ( i − 1 − k ) ) = 1 f(i-1-k,j-(k+1)(i-1-k))=1 f(i−1−k,j−(k+1)(i−1−k))=1 It was established .
Complete code :
#include<bits/stdc++.h>
#define FAST ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define INF 0x3f3f3f3f
typedef long long ll;
const int maxn = 1e5+5;
using namespace std;
int n;
int dp[1001][1001];
int main()
{
FAST;
for (int i=1; i<=20; i++) dp[i][0]=1;
for (int i=2; i<=20; i++)
{
for (int j=1; j<=200; j++)
for (int k=0; k<=i-1; k++)
if (dp[i-1-k][j-(k+1)*(i-1-k)]) dp[i][j]=1;
}
while(cin>>n)
{
for (int i=0; i<=n*(n-1)/2-1; i++)
if (dp[n][i]) cout<<i<<' ';
cout<<n*(n-1)/2<<endl;
}
return 0;
}
边栏推荐
猜你喜欢
![[initial launch] there are too many requests at once, and the database is in danger](/img/c1/807575e1340b8f8fe54197720ef575.png)
[initial launch] there are too many requests at once, and the database is in danger

Cadence spb17.4 - Allegro - optimiser la spécification de l'angle de connexion de la polyligne pour une seule ligne électrique - polyligne à arc
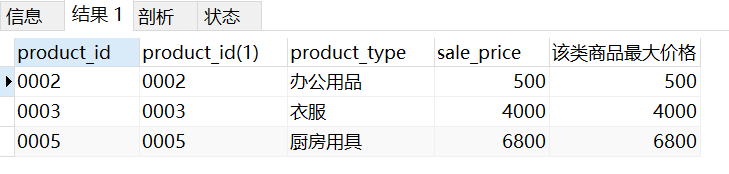
SQL programming task04 job - set operation
![[launch] redis Series 2: data persistence to improve availability](/img/f4/5bc7ca3e17c6656e71df515182842e.png)
[launch] redis Series 2: data persistence to improve availability

SAP ui5 application development tutorial 102 - detailed explanation of the print function of SAP ui5 applications
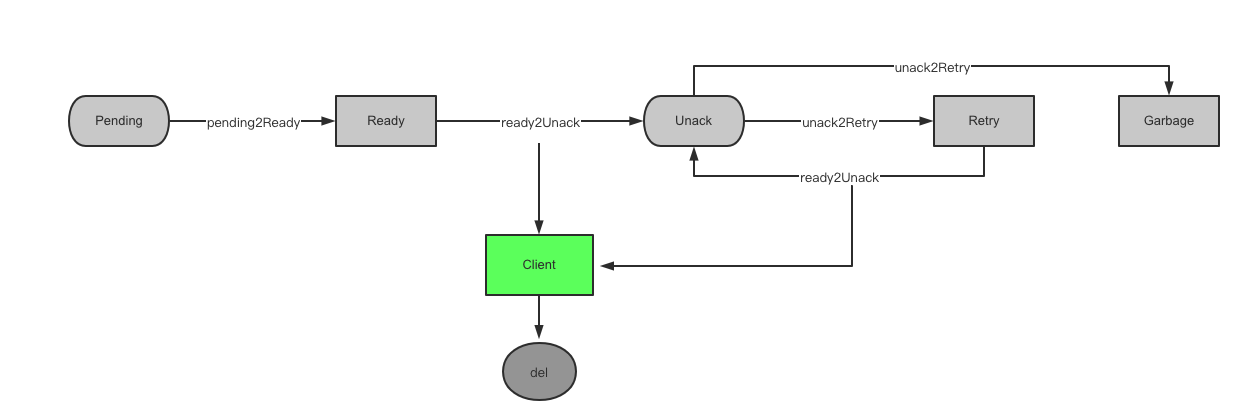
A hundred lines of code to realize reliable delay queue based on redis

Wallys/DR7915-wifi6-MT7915-MT7975-2T2R-support-OpenWRT-802.11AX-supporting-MiniPCIe

OSPF综合实验

BGP federal comprehensive experiment

How to set the power-off auto start of easycvr hardware box
随机推荐
Which platform is safer to buy stocks on?
Cadence spb17.4 - Chinese UI settings
How about precious metal spot silver?
Population standard deviation and sample standard deviation
Yyds dry goods counting tail recursion is better than recursion
Random decoding NLP
Project directory navigation
Dual cross domain: access allow origin header contains multiple values "*, *", but only one is allowed
C#.NET万能数据库访问封装类(ACCESS、SQLServer、Oracle)
Shell logs and printouts
It's still like this
Quelle est la structure et la façon dont les données sont stockées dans la base de données?
A hundred lines of code to realize reliable delay queue based on redis
一文读懂基于Redis的Amazon MemoryDB数据库
Vector 6 (inheritance)
LINQ query
leetcode 91. Decode Ways 解码方法(中等)
Fluentd is easy to use. Combined with the rainbow plug-in market, log collection is faster
Shell 日志与打印输出
Pat class A - 1012 the best rank (PIT)