Markov random field: definition, properties, maximum a posteriori probability problem, energy minimization problem

Markov random Airport

Markov random Airport Also known as Markov Network （Markov random field (MRF), Markov network or undirected graphical model） Yes. Set of random variables with Markov attributes , It is described by an undirected graph .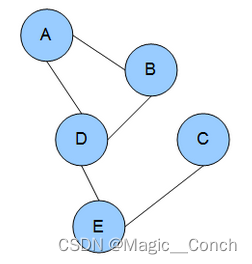
The above figure is an example of Markov random field , Edges represent dependencies . Above picture ,A Depend on B、D,C Depend on E, And so on .

Definition

For a given undirected graph $G=(V,E)$ And one by V Set of indexed random variables $X={\left(X_v\right)}_{v\in V}$, If they satisfy local Markov properties , Just say X It's about G Markov random fields of .

Pre knowledge ： Conditions are independent

Use the example above to illustrate conditional independence ： Staying in bed and getting up late depend on each other , Getting up late and being late depend on each other , But if you know the probability of getting up late in advance , Staying in bed and getting up late are mutually independent .

Three properties of Markov

1. Pairwise Markov properties Pairwise Markov property： Given all the other variables , Any two non adjacent variables are conditionally independent .（ For example, I know the other three variables , Staying in bed and being late are independent of each other .）
   $$X_u\perp X_v\mid X_{V\backslash \{u,v\}}$$
2. Local Markov properties Local Markov property： All adjacent variables of a given variable , This variable condition is independent of all other variables （ In the following formula ,$N(v)$ yes v Adjacency set of ）.（ For example, knowing the variables of getting up late and being depressed , Staying in bed and being late 、 Being scolded is independent of each other .）
   $$X_v\perp X_{V\backslash \mathrm{N}[v]}\mid X_{\mathrm{N}(v)}$$
3. Global Markov properties ： Given a separate subset , Subsets of any two random variables are conditionally independent （ In the following formula , Any A Set the node to B The path of the node of the set must go through S Nodes in ）.（ Given late , Stay in bed 、 Get up late 、 The variables in the set of depressed and scolded are independent of each other .）
   $$X_A\perp X_B\mid X_S$$

In the above formula ,$\perp$ Represents mutual independence ,$\mid$ For conditions ,$\backslash$ Represents the difference set .

The relationship between the three properties of Markov

overall situation $>$ Local $>$ Pair , However, the above three properties are equivalent for positive distribution （ It's not 0 Probability distribution ）.

The relationship between these three properties is better understood by the following formula ：

• Pairwise Pair ： For any unequal or nonadjacent $i,j\in V$, Yes $X_i\perp X_j\mid X_{V\backslash \{i,j\}}$.
• Local Local ： To any $i\in V$ and Does not contain or relate to $i$ Adjacent sets $J\subset V$, Yes $X_i\perp X_J\mid X_{V\backslash (\{i\}\cup J)}$
• Global overall situation ： For any disjoint and nonadjacent $I,J\subset V$, Yes $X_I\perp X_J\mid X_{V\backslash (I\cup J)}$.

Clique decomposition Clique factorization

It is difficult to establish a conditional probability distribution directly according to the properties of Markov random fields , So the more commonly used kind of Markov random field is Can be decomposed according to the clique of the graph .

Clique group ： Clique is a subset of vertices of an undirected graph , In this subset , Every two vertices are adjacent .

The more commonly used Markov random field formula is as follows ：
$$P(X=x)=\prod _{C\in \mathrm{cl}(G)}{\varphi }_C\left(x_C\right)$$

In the above formula ,X Is the joint probability density ;x Not a single value , It's a set of values ;$cl(G)$ yes G The group of ; function ${\varphi }_C$ It's a potential function , It can mean a ball （ The vertices ） Potential of , It can also refer to factors （ edge ） Potential of , It depends on the actual modeling needs .

Markov random field joint probability density can be further expressed as the following decomposition mode

$$P\left(x_1,\dots ,x_n\right)=\frac{1}{Z_{\Phi }}\prod _{i=1}{\varphi }_i\left(D_i\right)$$

among ,$Z_{\Phi }$ Is the normalization factor of the joint probability distribution , It is usually called partition function (partition function).$D_i$ Is a collection of random variables , factor ${\varphi }_i\left(D_i\right)$ It is a mapping from the set of random variables to the field of real numbers , be called Potential function or factor
$$\begin{array}{rl}& \Phi =\left\{{\varphi }_i\left(D_i\right),\dots ,{\varphi }_K\left(D_K\right)\right\}\\ & \tilde{p}\left(x_1,\dots ,x_n\right)=\prod _{i=1}{\varphi }_i\left(D_i\right)\\ & Z_{\Phi }=\sum _{x_1,\dots ,x_n}\tilde{p}\left(x_1,\dots ,x_n\right)\end{array}$$

Example of Markov random field

The local potential function is not directly related to the edge probability density .

Paired Markov random fields and their applications

The formula of paired Markov random fields is as follows ：
$$\frac{1}{Z_{\Phi }}\prod _{p\in V}{\varphi }_p\left(x_p\right)\prod _{(p,q)\in E}{\varphi }_{pq}\left(x_p,x_q\right)$$
Image processing problems can often be defined in MRF The maximum a posteriori probability problem on ：

$$\underset{\mathbf{x}}{\max }p(\mathbf{x})\propto \prod _{p\in V}{\varphi }_p\left(x_p\right)\prod _{(p,q)\in E}{\varphi }_{pq}\left(x_p,x_q\right)$$

The o $p(x)$ At the very least ,x The value of , As shown in the figure below .

The maximum a posteriori reasoning problem is equivalent to the energy minimization problem , Make ${\theta }_p\left(x_p\right)=-\log {\varphi }_p\left(x_p\right),{\theta }_{pq}\left(x_p,x_q\right)=-\log {\varphi }_{pq}\left(x_p,x_q\right)$, Yes ：
$$\underset{x}{\min }E(\mathbf{x})=\sum _{p\in V}{\theta }_p\left(x_p\right)+\sum _{(p,q)\in E}{\theta }_{pq}\left(x_p,x_q\right)$$

Assumption of potential function ： The value of continuous pixels is continuous .