当前位置:网站首页>[digital signal processing] linear time invariant system LTI (judge whether a system is a "non time variant" system | case 3)
[digital signal processing] linear time invariant system LTI (judge whether a system is a "non time variant" system | case 3)
2022-06-23 14:09:00 【Hanshuliang】
List of articles
One 、 Judge whether the system is " Non time varying "
1、 Case 2
Given Input sequence x ( n ) = { 0 , 1 , 2 , 3 , 4 , 5 , 0 } x(n) = \{ 0, 1 , 2, 3, 4, 5 , 0 \} x(n)={ 0,1,2,3,4,5,0} , n n n Value − 1 -1 −1 ~ 5 5 5

Determine the output sequence y ( n ) = x ( n 2 ) y(n) = x(n^2) y(n)=x(n2) Of " Transformation " Operation Yes No " Time does not change " Of ;
y ( n ) = x ( n 2 ) y(n) = x(n^2) y(n)=x(n2) Change operation :
y ( n ) y(n) y(n) Only in n = − 1 , 0 , 1 , 2 n = -1 , 0 , 1 , 2 n=−1,0,1,2 When the value is taken , It's worth it ,
If n = 3 n = 3 n=3 , n 2 = 9 n^2 = 9 n2=9 , x ( 9 ) x(9) x(9) No value ;
If n = 4 n = 4 n=4 , n 2 = 16 n^2 = 16 n2=16 , x ( 16 ) x(16) x(16) No value ;
If n = 5 n = 5 n=5 , n 2 = 25 n^2 = 25 n2=25 , x ( 10 ) x(10) x(10) No value ;
therefore , After normal transformation , y ( n ) y(n) y(n) The value is n = 0 , 1 , 2 n = 0 , 1 , 2 n=0,1,2 The value of time ,
When n = − 1 n = -1 n=−1 when , y ( n ) = x ( n 2 ) = x ( ( − 1 ) 2 ) = x ( 1 ) = 2 y(n) = x(n^2) = x((-1)^2) = x(1) = 2 y(n)=x(n2)=x((−1)2)=x(1)=2 ;
When n = 0 n = 0 n=0 when , y ( n ) = x ( n 2 ) = x ( 0 2 ) = x ( 0 ) = 1 y(n) = x(n^2) = x(0^2) = x(0) = 1 y(n)=x(n2)=x(02)=x(0)=1 ;
When n = 1 n = 1 n=1 when , y ( n ) = x ( n 2 ) = x ( 1 2 ) = x ( 1 ) = 2 y(n) = x(n^2) = x(1^2) = x(1) = 2 y(n)=x(n2)=x(12)=x(1)=2 ;
When n = 2 n = 2 n=2 when , y ( n ) = x ( n 2 ) = x ( 2 2 ) = x ( 4 ) = 5 y(n) = x(n^2) = x(2^2) = x(4) = 5 y(n)=x(n2)=x(22)=x(4)=5 ;
among − 1 -1 −1 and 1 1 1 The square of is 1 1 1 , Merge into one ;
x ( n ) x(n) x(n) The value after normal transformation is :
y ( n ) = { 1 , 2 , 5 } y(n) = \{ 1, 2, 5 \} y(n)={ 1,2,5}
① Time invariant system concept
Time invariant system ( time-invariant ) : System features , Does not change with time ;
y ( n − m ) = T [ x ( n − m ) ] y(n - m) = T[x(n-m)] y(n−m)=T[x(n−m)]
After input delay , The output is also delayed ;
And " Time does not change " The system corresponds to " time varying " System ;
② First transform and then shift
take " Output sequence " Shift , First " Transformation " after " displacement " ;
First the " Input sequence " Conduct " Transformation " operation , obtain " Output sequence " , Then on Output sequence Conduct " displacement " operation ;
among " Transformation " refer to , Discrete time systems , take " Input sequence " Transformation by " Output sequence " , Input sequence To Output sequence Operation between , yes " Transformation " ;
Change operation : First the Input sequence x ( n ) x(n) x(n) Conduct Transformation operation , obtain Output sequence x ( n 2 ) x(n^2) x(n2) ,
Shift operation : then Yes x ( n 2 ) x(n^2) x(n2) Output sequence Shift n − n 0 n - n_0 n−n0 obtain x ( ( n − n 0 ) 2 ) x((n-n_0)^2) x((n−n0)2) ,
The complete operation process is as follows :
y ( n − n 0 ) = x ( ( n − n 0 ) 2 ) y(n - n_0) = x((n-n_0)^2) y(n−n0)=x((n−n0)2)
First change , After transformation, the output is :
y ( n ) = { 1 , 2 , 5 } y(n) = \{ 1, 2, 5 \} y(n)={ 1,2,5}
The value of post shift is : Move one bit to the right ;
y ( n − 1 ) = { 0 , 1 , 2 , 5 } y(n-1) = \{ 0, 1, 2, 5 \} y(n−1)={ 0,1,2,5}
③ Shift first and then transform
take " Input sequence " Shift , Shift first , take " Input sequence x ( n ) x(n) x(n) " to " displacement " operation , obtain new " Input sequence " by x ( n − n 0 ) x(n-n_0) x(n−n0) , then The new input sequence is " Transformation " operation , obtain " Output sequence " ;
The transformation process is T [ x ( n − n 0 ) ] = x ( n 2 − n 0 ) T[x(n - n_0)] = x(n^2 - n_0) T[x(n−n0)]=x(n2−n0) , Transformation time , Just to n n n Value to n 2 n^2 n2 , n 0 n_0 n0 Fixed value ;
x ( n − n 0 ) x(n-n_0) x(n−n0) Transformation time , Only will n n n multiply 2 2 2 , n 0 n_0 n0 unchanged , The transformation result is as follows x ( 2 n − n 0 ) x(2n - n_0) x(2n−n0) ;
The whole process is as follows :
T [ x ( n − n 0 ) ] = x ( n 2 − n 0 ) T[x(n - n_0)] = x(n^2 - n_0) T[x(n−n0)]=x(n2−n0)
First the x ( n ) = { 0 , 1 , 2 , 3 , 4 , 5 , 0 } x(n) = \{ 0, 1 , 2, 3, 4, 5 , 0 \} x(n)={ 0,1,2,3,4,5,0} , n n n Value − 1 -1 −1 ~ 5 5 5 , Shift right , The shifted sequence :
x ( n ) = { 0 , 1 , 2 , 3 , 4 , 5 } x(n) = \{ 0, 1 , 2, 3, 4, 5 \} x(n)={ 0,1,2,3,4,5} n n n Value 0 0 0 ~ 6 6 6 , The shifted sequence schema is as follows :

Shift right 1 after , n n n Value From the original − 1 -1 −1 ~ 5 5 5 Change into 0 0 0 ~ 6 6 6 ,
y ( n ) y(n) y(n) Only in n = 0 , 1 , 2 n = 0 , 1 , 2 n=0,1,2 When the value is taken , It's worth it ,
If n = 3 n = 3 n=3 , n 2 = 9 n^2 = 9 n2=9 , x ( 9 ) x(9) x(9) No value ;
If n = 4 n = 4 n=4 , n 2 = 16 n^2 = 16 n2=16 , x ( 16 ) x(16) x(16) No value ;
If n = 5 n = 5 n=5 , n 2 = 25 n^2 = 25 n2=25 , x ( 10 ) x(10) x(10) No value ;
therefore , After normal transformation , y ( n ) y(n) y(n) The value is n = 0 , 1 , 2 n = 0 , 1 , 2 n=0,1,2 The value of time ,
When n = 0 n = 0 n=0 when , y ( n ) = x ( n 2 ) = x ( 0 2 ) = x ( 0 ) = 0 y(n) = x(n^2) = x(0^2) = x(0) = 0 y(n)=x(n2)=x(02)=x(0)=0 ;
When n = 1 n = 1 n=1 when , y ( n ) = x ( n 2 ) = x ( 1 2 ) = x ( 1 ) = 1 y(n) = x(n^2) = x(1^2) = x(1) = 1 y(n)=x(n2)=x(12)=x(1)=1 ;
When n = 2 n = 2 n=2 when , y ( n ) = x ( n 2 ) = x ( 2 2 ) = x ( 4 ) = 4 y(n) = x(n^2) = x(2^2) = x(4) = 4 y(n)=x(n2)=x(22)=x(4)=4 ;
x ( n − 1 ) x(n - 1) x(n−1) The value after normal transformation is :
T ( x ( n − 1 ) ) = { 0 , 1 , 4 } T(x(n -1 )) = \{ 0, 1, 4 \} T(x(n−1))={ 0,1,4}
④ Conclusion
First " Transformation " after " displacement " , The result is x ( ( n − n 0 ) 2 ) x((n-n_0)^2) x((n−n0)2) , Output sequence by y ( n − 1 ) = { 0 , 1 , 2 , 5 } y(n-1) = \{ 0, 1, 2, 5 \} y(n−1)={ 0,1,2,5}
First " displacement " after " Transformation " , The result is x ( n 2 − n 0 ) x(n^2 - n_0) x(n2−n0) , The output sequence is T ( x ( n − 1 ) ) = { 0 , 1 , 4 } T(x(n -1 )) = \{ 0, 1, 4 \} T(x(n−1))={ 0,1,4}
The system is " Time varying system " ;
边栏推荐
- Shell process control - 39. Special process control statements
- 微信小程序之input前加图标
- 4-way telephone +1-way Gigabit Ethernet 4-way PCM telephone optical transceiver
- 【深入理解TcaplusDB技术】Tmonitor系统升级
- IEEE Transaction期刊修改过程记录
- 智能数字看板解决方案
- 2022 soft science university professional ranking released! Xi'an electric AI ranked higher than Qingbei, and Nantah ranked first in the country!
- KDD 2022 | epileptic wave prediction based on hierarchical graph diffusion learning
- Binding events of wechat applet in wx:for
- Common usage of OS (picture example)
猜你喜欢

How to write vite plug-ins
![Web technology sharing | [Gaode map] to realize customized track playback](/img/b2/25677ca08d1fb83290dd825a242f06.png)
Web technology sharing | [Gaode map] to realize customized track playback

Basic data types of C language and their printouts
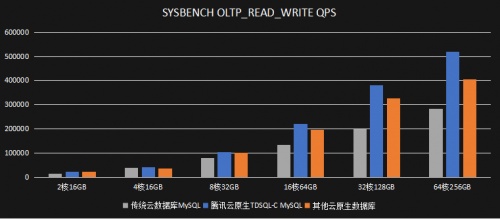
Tencent cloud tdsql-c heavy upgrade, leading the cloud native database market in terms of performance

【深入理解TcaplusDB技术】Tmonitor后台一键安装

What is the principle of live CDN in the process of building the source code of live streaming apps with goods?

Wechat applet pop up the optional menu from the bottom

实战 | 如何制作一个SLAM轨迹真值获取装置?

Modelsim 安装步骤详解

OpenVINOTM 2022.1中AUTO插件和自动批处理的最佳实践
随机推荐
Add Icon before input of wechat applet
【深入理解TcaplusDB技术】一键安装Tmonitor后台
4-way telephone +1-way Gigabit Ethernet 4-way PCM telephone optical transceiver
KS003基于JSP和Servlet实现的商城系统
MySQL single database and table splitting using MYCAT
Develop a powerful tool for increasing efficiency - vscode plug-in sharing in 2022
IEEE Transaction期刊修改过程记录
Interrupt and polling
CRMEB 二开短信功能教程
vulnhub靶机Os-hackNos-1
构建英特尔 DevCloud
Sqlserver2008r2 failed to install DTS component
前AMD芯片架构师吐槽,取消 K12 处理器项目是因为 AMD 怂了!
白皮书丨英特尔携手知名RISC-V工具提供商Ashling,着力扩展多平台RISC-V支持
kali使用
Gary Marcus wrote: three perspectives from linguists that AI researchers need to know
Assembly language interrupt and external device operation --06
[deeply understand tcapulusdb technology] one click installation of tmonitor background
父母-子女身高数据集的线性回归分析
Win the championship for 2 consecutive years! ZABBIX ranked first in a number of monitoring software in 2022