Étalonnage de la caméra (objectif et principe d'étalonnage)

1.Objet de l'étalonnage de la caméra：

（1）L'un est de corriger la distorsion de l'image causée par la distorsion de la lentille,Par exemple,Ligne droite dans la réalité,Convexe ou concave après prise d'image,Cette condition peut être corrigée après l'étalonnage de la caméra;

（2） L'autre est basé sur le tournage 2 - D Images pour reconstruire une scène 3D ,Parce que le processus d'étalonnage est une transformation mathématique à travers une série de points 3D et ses points d'image 2D correspondants,Trouver les paramètres internes et externes de la caméra.

Caméra étalonnée,On peut mesurer la distance、Reconstruction de scènes 3D, etc.

2.Quatre systèmes de coordonnées

        L'un des objectifs de l'étalonnage de la caméra est d'établir la correspondance entre les points de coordonnées de l'objet du monde tridimensionnel au plan d'imagerie,Voici donc les quatre systèmes de coordonnées：

Système mondial de coordonnées：Système de coordonnées du monde 3D défini par l'utilisateur,Introduit pour décrire la position de la cible dans le monde réel et la position de la caméra.

Système de coordonnées de la caméra：Le système de coordonnées établi sur la caméra,Défini pour décrire la position de l'objet du point de vue de la caméra,En tant que système de coordonnées et d'images pour communiquer le monde/L'anneau central du système de coordonnées pixels.

Système de coordonnées d'image：Pour décrire la transmission projetée d'un objet du système de coordonnées de la caméra au système de coordonnées de l'image pendant le processus d'imagerie,Pour obtenir plus facilement les coordonnées sous le système de coordonnées pixels.

Système de coordonnées pixels：Pour décrire les points d'image sur l'image numérique après l'imagerie de l'objet（Photos）Les coordonnées de,C'est le système de coordonnées dans lequel se trouve l'information que nous avons réellement lue à partir de la caméra,Les unités sont（Nombre de pixels）.

3.Conversion des coordonnées

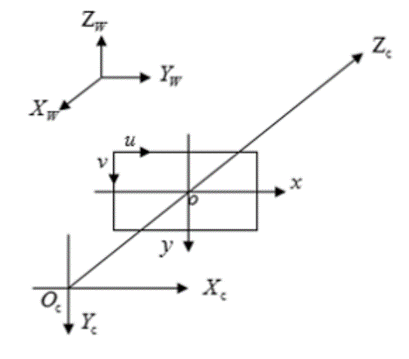
Système mondial de coordonnées：Xw、Yw、Zw.

Système de coordonnées de la caméra： Xc、Yc、Zc.

Système de coordonnées d'image：x、y.

Système de coordonnées pixels：u、v.

        Parmi eux, Du système de coordonnées de la caméra Z L'axe coïncide avec l'Axe optique , Et perpendiculaire au plan du système de coordonnées d'image et passant par l'origine du système de coordonnées d'image , La distance entre le système de coordonnées de la caméra et le système de coordonnées de l'image est la distance focale f. Plan du système de coordonnées pixels u-v Et le plan du système de coordonnées d'image x-yCoïncidence, Mais l'origine du système de coordonnées pixels est dans le coin supérieur gauche de l'image .

3.1World Coordinate System to Camera Coordinate System

Supposons qu'il tourne autour dexRotation de l'arbre（Dans le sens contraire des aiguilles d'une montre）

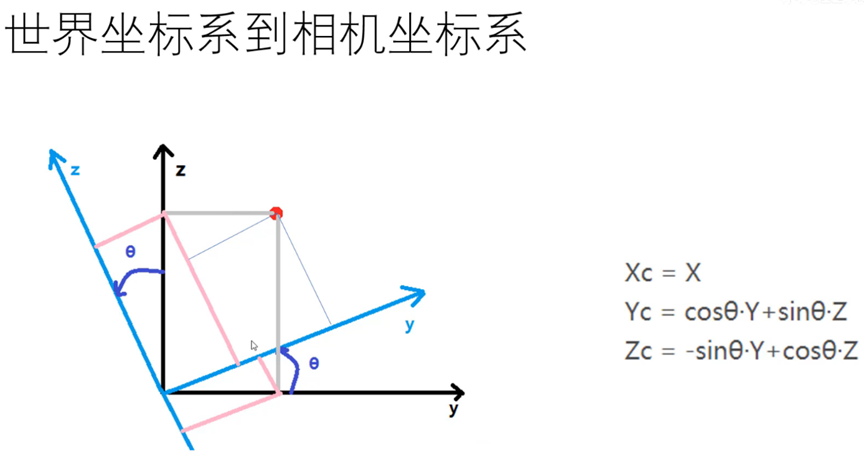
Et ainsi de suite., Tourner autour d'autres axes （Dans le sens horaire）

Système de coordonnées du monde au système de coordonnées de la caméra 6Des degrés de liberté, Traduction en plus de la rotation

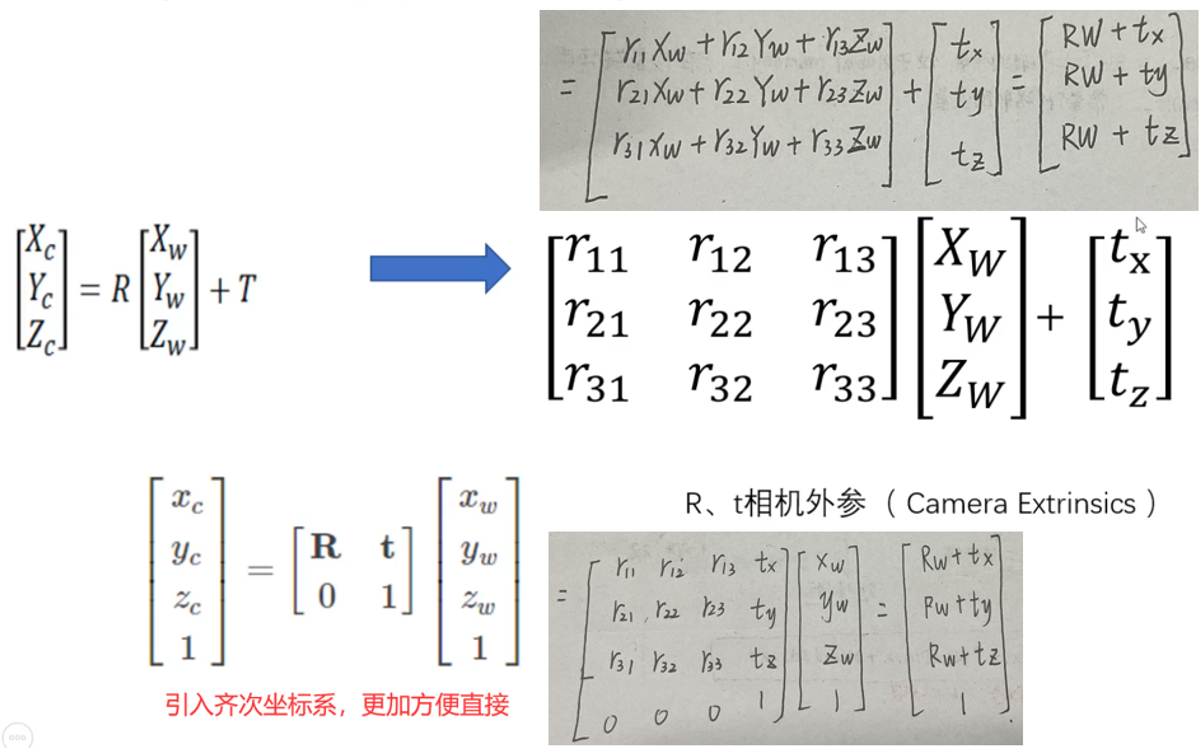
3.2 Système de coordonnées de la caméra au système de coordonnées de l'image

3.3 Système de coordonnées d'image au système de coordonnées pixels

L'origine du système de coordonnées de l'image est au centre de l'image ,Unitémm.

L'origine du système de coordonnées pixels est dans le coin supérieur gauche de l'image ,Les unités sont en pixelsPixel（- Oui.）.

dx,dy: Est un paramètre inhérent au capteur , Représente le nombre de millimètres par Pixel .

u0,v0： Représente l'offset de l'origine du système de coordonnées d'image par rapport au système de coordonnées pixels ,Les unités sont en pixels.

3.4 Tout le processus de transformation du système mondial de coordonnées en système de coordonnées pixels

 Jusqu'ici., Pour reconstruire une scène 3D à partir d'une image 2D prise , Alors, demandez une référence interne M1Et extraginsengM2.

 3.5Zhang zhengyou Calibration Method

 

 

 

Singularité（Homography）Transformation.Il peut être interprété simplement comme étant utilisé pour décrire la cartographie de position d'un objet entre le système mondial de coordonnées et le système de coordonnées pixels.La matrice de transformation correspondante est appelée matrice de contrainte unique.

 

 

 

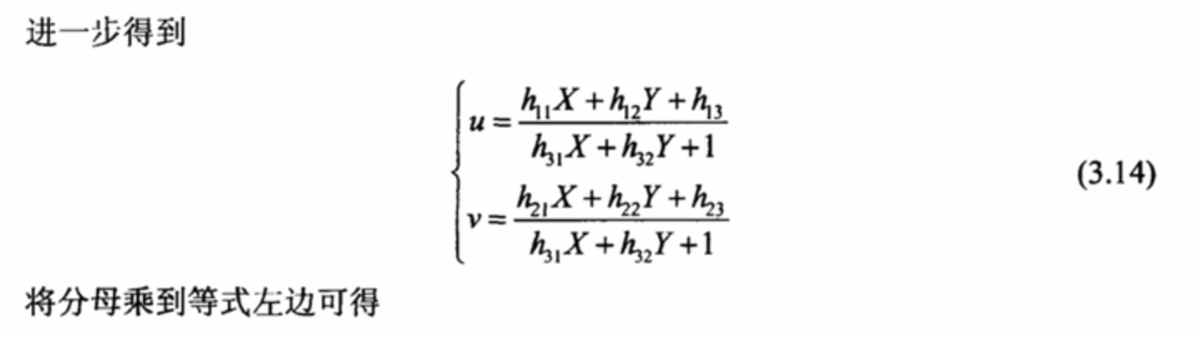
Comment obtenir une matrice de réponse unique à partir d'un diagramme d'étalonnage ？

Après une série d'introductions , Nous devrions avoir une idée générale de la façon de calculer la matrice de Singleton à partir des cartes d'étalonnage imprimées et des photos prises H. Résumons les grandes lignes du processus .

1. Imprimer un dessin d'étalonnage du vérificateur , Collez - le sur la surface d'un objet plat .

2. Prenez des photos d'un ensemble de damiers dans différentes directions , On peut le faire en déplaçant la caméra , Vous pouvez également déplacer l'image d'étalonnage pour .

3. Pour chaque image prise , Détecter les points caractéristiques de tous les damiers de l'image （Corner point, C'est l'intersection de l'échiquier noir et blanc dans l'image ci - dessous , Il y a un point d'angle dans le cercle rouge du milieu ,Quatre diagonales（ Rouge, jaune, bleu, vert ） C'est le coin le plus spécial ）. Nous définissons les dessins d'échiquier imprimés dans le système mondial de coordonnées Zw=0Sur le plan de, L'origine du système mondial de coordonnées est située dans le coin fixe de la feuille d'échiquier de gauche （ Comme le point jaune dans l'image ci - dessous ）. L'origine du système de coordonnées pixels est située dans le coin supérieur gauche de l'image de droite .

Parce que dans le dessin d'étalonnage du échiquier Tous les Les coordonnées spatiales des points d'angle sont connues , Les coordonnées pixels de ces points d'angle correspondant aux points d'angle de l'image d'étalonnage photographiée sont également connues , Si on avait ça N>=4 Paires de points correspondants （ Plus les calculs sont robustes ）,Peut être basé surLM La méthode isooptimisée donne Une matrice de réponse unique dans cette perspective H. Bien sûr, il n'est généralement pas nécessaire d'écrire une fonction pour réaliser la matrice de calcul ,OpenCV Il y a des fonctions prêtes à l'emploi qui peuvent être appelées .

Mais, Ce qui précède n'est qu'une dérivation théorique , Dans un scénario d'application réel , Les paires de points que nous calculons contiennent du bruit . Par exemple, la position du point s'écarte de quelques pixels , Il y a même une mauvaise correspondance entre les points caractéristiques ,Si seulement4 Paires de points pour calculer la matrice de réponse unique , Ça va faire une grosse erreur .Donc,, Pour rendre les calculs plus précis , En général, on utilise beaucoup plus de 4 Paires de points pour calculer la matrice de réponse unique . De plus, il est souvent difficile d'obtenir la solution optimale des équations ci - dessus en utilisant la méthode linéaire directe , Par conséquent, d'autres méthodes d'optimisation sont généralement utilisées dans la pratique ,Comme la décomposition de la valeur singulière、Levenberg-Marquarat（LM）Algorithmes

Matrice de contrainte unique obtenue par la méthode ci - dessus HAprès,Voici commentH Inverser les paramètres internes et externes de la caméra

Par dessus2.28Avec2.29Oui.：

 ​​​

  Peut être calculé par lui - mêmeBEst une Matrice diagonale,Alors...BSeulement6Inconnu,Donc le vecteurbParamètres6Paramètres

 

Quelques images deBCapture d'écran vidéo de la station,Bienvenue à l'échange et à l'apprentissage.

Il est fortement recommandé de lire cet article ： Explication détaillée du principe mathématique de la méthode d'étalonnage Zhang zhengyou pour l'étalonnage de la caméra （Y comprispythonCode source） - Oui.