当前位置:网站首页>The k-th element in the array [heap row + actual time complexity of heap building]
The k-th element in the array [heap row + actual time complexity of heap building]
2022-06-28 15:22:00 【REN_ Linsen】
Stack row + Time complexity of reactor building
Preface
The heap can be arranged without complete sorting , Take second place K Big element , But the same is true of selective sorting .
So who will run faster ? When building a reactor , Need to adjust n/2 Time , The maximum depth of each time is log2(n), The first visual impression is to build a pile T(n) = O(nlgon), It's not .
Heap discharge k The time of the big element = Build time + take k The time of the first element = (O(n) - O(log2n) - 1) + O(klog2n) = O(n);
Select sort to get k The time of the big element = O(kn) = O(n).
because (O(n) - O(log2n) - 1) + O(klog2n) <O(kn), So stack faster .
The proof is in the comments before the second part of the code .
One 、 The... In the array K Big element
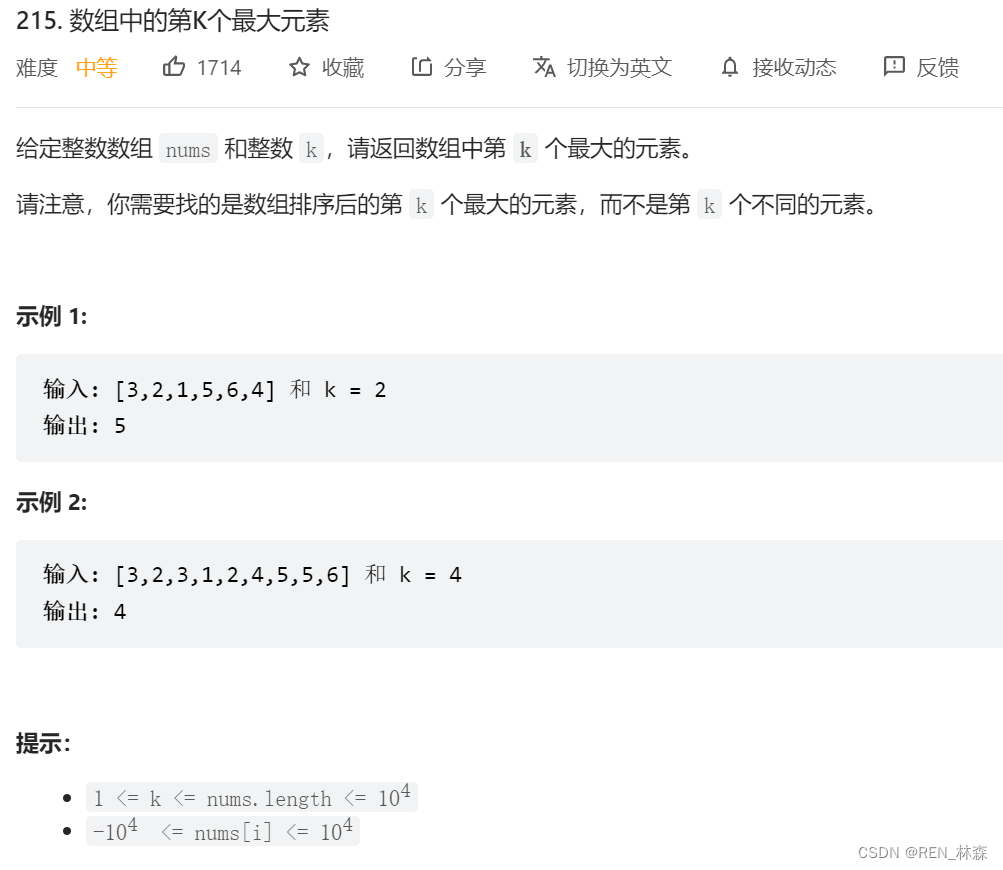
Two 、 Proof of reactor building complexity
prove : Take the full binary tree with the most nodes as an example , Tree height is h,
Set the current layer as k, Then this layer has 2^(k - 1)^ Nodes , Each node needs to be adjusted h - k The depth of the .
therefore ,T(n) = 20 * (h - 1) + 21 * (h - 2) +…+2^(h - 2) * 1, Obviously, it is a typical difference ratio sequence , Just offset and subtract .
2T(n) = 21 * (h - 1) + 22 * (h - 2) +…+2^(h - 2)^ * 2 + 2^(h - 1) * 1,
The difference between the two formulas is T(n) = 2h - h - 1, notes :h = log2(n), therefore T(n) = O(n) - O(log2(n)) - 1 = O(logn)
notes : Computational complexity , The premise is that n Large enough , If n Very small , There is no complexity , direct O(1)
3、 ... and 、 Quick line up / Priority queue / Stack row
package everyday.medium;
import java.util.PriorityQueue;
// No k The biggest element .
public class FindKthLargest {
/* target: Take the second in the array K Big element , Put the array in order , take nums[k - 1] that will do , But the time complexity O(nlogn), Not an option . Selection sort , Select the first K individual , Time complexity O(kn), namely O(n), feasible . Stack row , It takes time to build a pile O(nlogn), Choose the first k Big , flowers O(klogn), Time complexity O( ), Is not workable . Why does it take to build a pile O(nlogn)? Our intuitive feeling , To adjust n/2 Time ( Adjust from the penultimate line ), Adjust downward each time O(logn)( Naturally took the biggest one ). So building a pile takes O(nlogn). But this is an illusion . The actual time complexity is Tn = 2^log2(n)^ - log2(n) - 1 =O(n) - O(logn) = O(n)( When n When a large ) prove : Take the full binary tree with the most nodes as an example , Tree height is h, Set the current layer as k, Then this layer has 2^(k - 1)^ Nodes , Each node needs to be adjusted h - k The depth of the . therefore ,T(n) = 2^0^ * (h - 1) + 2^1^ * (h - 2) +...+2^(h - 2) * 1, Obviously, it is a typical difference ratio sequence , Just offset and subtract . 2T(n) = 2^1^ * (h - 1) + 2^2^ * (h - 2) +...+2^(h - 2)^ * 2 + 2^(h - 1) * 1, The difference between the two formulas is T(n) = 2^h^ - h - 1, notes :h = log2(n), therefore T(n) = O(n) - O(log2(n)) - 1 = O(logn) notes : Computational complexity , The premise is that n Large enough , If n Very small , There is no complexity , direct O(1) */
// Selection sort -- Although it is O(n), But time is Tn = kn, Compared with stacking ,Tn = n - log(n+1) + klogn, Still a lot slower .
public int findKthLargest(int[] nums, int k) {
for (int i = 0; i < k; i++) {
// choice
int max = nums[i], idx = i;
for (int j = i + 1; j < nums.length; j++) {
if (max < nums[j]) {
max = nums[j];
idx = j;
}
}
// swap
int t = nums[idx];
nums[idx] = nums[i];
nums[i] = t;
}
// Value
return nums[k - 1];
}
// Stack row , skilled API, Priority queue , The whole big top pile .
public int findKthLargest2(int[] nums, int k) {
// Big pile top
PriorityQueue<Integer> que = new PriorityQueue<>((o1, o2) -> o2 - o1);
// Add elements
for (int num : nums) que.offer(num);
// The first 1 - (k-1) Large elements are taken out
for (int i = 0; i < k - 1; i++) que.poll();
// Take the first place K Big
return que.poll();
}
// Stack row ,API There are too many encumbrances , Direct stacking .
public int findKthLargest3(int[] nums, int k) {
// Building the heap , Start from the node with children on the penultimate layer .
for (int i = nums.length - 1 >>> 1; i >= 0; i--) adjustHeap(nums, i, nums.length);
// Front row K A big element comes out .
int i = 0;
do {
// swap
int t = nums[0];
nums[0] = nums[nums.length - 1 - i];
nums[nums.length - 1 - i] = t;
// Adjust the heap , Make the top of the heap the largest element .
if (++i >= k) break;
adjustHeap(nums, 0, nums.length - i);
} while (true);
// Take the first place k The biggest element
return nums[nums.length - k];
}
// Stack core : Adjust the heap
private void adjustHeap(int[] nums, int k, int end) {
int ori = nums[k]; // Remember the original elements to adjust .
// Keep adjusting downward
for (int i = (k << 1) + 1; i < end; i = (i << 1) + 1) {
// Whether the left child or the right child is older .
if (i + 1 < end && nums[i + 1] > nums[i]) ++i;
// See if it is necessary to exchange with the child .
if (ori >= nums[i]) break;
// Downward adjustments
nums[k] = nums[i];
// Get the new position of the original element .
k = i;
}
// Put the original element in the space it was last swapped to .
nums[k] = ori;
}
}
summary
1) The time complexity of building a heap is O(n), No O(nlogn).
2) Priority queue / Stack row / Selection sort .
reference
边栏推荐
- What! One command to get the surveillance?
- What! 一条命令搞定监控?
- Leike defense: 4D millimeter wave radar products are expected to be mass produced and supplied by the end of the year
- MIPS assembly language learning -02- logic judgment - foreground input
- QQ被盗号后群发黄图,大批用户“社死”
- Halcon basic summary (I) cutting pictures and rotating images
- Spark SQL generate JSON
- Power battery is divided up like this
- ROS21讲
- Calculator (force buckle)
猜你喜欢

隐私计算 FATE - 离线预测

SAP mts/ato/mto/eto topic 9: front and back desk operation in m+m mode, strategy 50, preparation of raw materials and semi-finished products in advance

Innovation and upgrading of supply chain system driven management mode in petrochemical industry and strengthening internal management of enterprises
PostgreSQL实现按年、月、日、周、时、分、秒的分组统计
Express模板引擎

Jackie Chan and fast brand, who is the Savior of Kwai?

Flutter简单实现多语言国际化
MySQL主从切换的超详细步骤
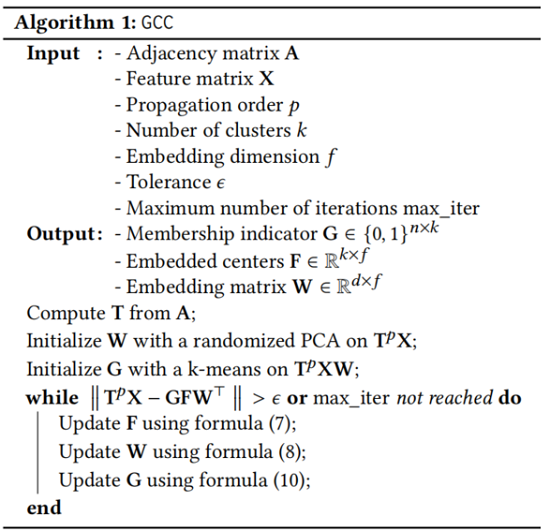
GCC efficient graph revolution for joint node representationlearning and clustering
Complete model training routine (I)
随机推荐
How can the digital intelligent supply chain management platform of the smart Park optimize process management and drive the development of the park to increase speed and quality?
R language ggplot2 visualization: use the patchwork package (directly use the plus sign +) to horizontally combine a ggplot2 visualization result and a piece of text content to form a final result gra
ROS知识点——话题消息的定义与使用
美国乔布斯,殁了;中国乔布斯,卖了
Li Kou today's question -522 Longest special sequence
Fleet |「後臺探秘」第 3 期:狀態管理
sql语句 练习题
Spacetutorial (continuous updating...)
DBMS in Oracle_ output. put_ Line output problem solving process
C语言学习-20-归并排序
Calculator (force buckle)
5000倍回报,南非报业投资腾讯赚了一个省
C语言基础语法
S2b2c system website solution for kitchen and bathroom electrical appliance industry: create s2b2c platform Omni channel commercial system
厨卫电器行业S2B2C系统网站解决方案:打造S2B2C平台全渠道商业系统
[C language] how to implement plural types
ROS21讲
Oracle11g数据库使用expdp每周进行数据备份并上传到备份服务器
Realization of a springboard machine
Web worker poll request

