leetcode LCP 10. Binary tree task scheduling

Title Description ：

Task scheduling optimization is one of the key tasks of computer performance optimization . When there are many tasks , Different scheduling strategies may result in different overall execution times , So it is very necessary to find an optimal scheduling scheme .

There are usually dependencies between tasks , That is, for a task , You need to finish his leading task first （ If it is not empty ）, To start the task . We guarantee that the task dependency is a binary tree , among root For root task ,root.left and root.right For his two leading tasks （ May is empty ）,root.val For its own execution time .

In a CPU When performing a task , We can suspend the execution of the current task at any time , And keep the current execution progress . The next time you continue the task , It will continue from the previous progress . The pause time may not be an integer .

Now? , The system has two CPU nucleus , That is, we can perform two tasks at the same time , But the same task cannot be performed on two cores at the same time . Given this task tree , Request the minimum time to complete all tasks .

Example 1：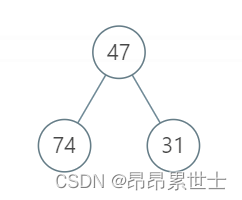

Input ：root = [47, 74, 31]

Output ：121

explain ： The left and right nodes of the root node can execute in parallel 31 minute , The rest 43+47 Minutes can only be executed serially , So the overall execution time is 121 minute .

Example 2：

Input ：root = [15, 21, null, 24, null, 27, 26]

Output ：87

Example 3：

Input ：root = [1,3,2,null,null,4,4]

Output ：7.5

Limit ：

1 <= Number of nodes <= 1000
1 <= Single node execution time <= 1000

analysis

This question is also practical hard The question of difficulty , At first, I thought it was very simple , Look at the use case 3 Come out 7.5 I was confused , After reading the comments, I learned 7.5 I still have no idea how I came here , After reading the solutions of several problems, I still don't understand the idea of solving problems , At last, I deduce it manually , To complete the problem , Five stars with proper thinking difficulty .

The system has two CPU nucleus , That is, we can perform two tasks at the same time , But the same task cannot be performed on two cores at the same time . This sentence is the core of this topic , If there is no use case 3 , Ninetypercent of the people will think that only the serial execution time and parallel execution time of the left and right subtrees are required , After a simple operation, the shortest execution time of the whole tree can be deduced . There are two CPU nucleus , During the execution of all tasks, either two cores perform different tasks at the same time , Or there is only one core working , The time when two cores work at the same time is called parallel time , The working time of a single core is called serial time . In the root A tree for roots , Let the serial time of the left subtree task execution be a, Parallel time is b; The serial time of the right subtree is c, Parallel time is d. Our first impression is to use the serial execution time of the two subtrees , such as a > c, We use it c Time parallel execution of , In this way, the time left for the serial operation of the left and right subtrees is only a - c 了 , add root Serial execution time of , Add all the parallel time to the total time . For example, use cases 3, Execute in parallel first 4 4, Time consuming 4, Try to execute in parallel what should be executed in serial 3 and 2, Parallel execution 2 Time , Serial execution 1 Time , Finally, it is executed serially 1, The total time thus obtained is 4 + 2 + 1 + 1 = 8, Greater than the output of the use case 7.5, It shows that this method is not optimal .

So use cases 3 How to implement it ？1 The child of is 3,2,2 The child of is 4,4. Our previous ideas are implemented in parallel 3,2 When 2 After execution 3 There is still left 1 Time can only be executed serially , Because two cores cannot perform the same task at the same time . The title has “ We can suspend the execution of the current task at any time , And keep the current execution progress ”, In this way, can we put 3 Of 1 Time is consumed , Then pause , Finally, talk to 2 Parallel execution together ？ The answer is yes . front 0.5 Time we execute in parallel 3 and 4, Then one core for another 4 To execute , such 1 Time passed ,2 The task time of my two children became 3.5, 3 The task time becomes 2. after 3.5 Time execution we execute two in parallel 3.5 The task of , After that 2 Time we execute in parallel 2 and 3（ There is only time left for the task 2）, Finally, the serial execution 1, The total time is 1 + 3.5 + 2 + 1 = 7.5.

For use cases 3 The simulation of can help us solve this problem , If you just look at the simulation process above , Will wonder , Why should we put 3 Remove two 0.5 Time and 4 To execute in parallel ,0.5 How did you get it ？ How do we split time when solving this problem ？ We might as well look at this process from a macro perspective ,1 Root node , First, we investigate its left subtree 3 Minimum execution time of , because 3 No child nodes , Serial only , So it takes time 3 After execution , Where serial time （ That is, a nuclear execution time ） yes 3, Parallel time （ Dual core execution time ） yes 0, Use the front letter to indicate that a = 3,b = 0;1 The serial execution time of the right subtree of is c = 2, Parallel execution time d = 4. This is obvious , According to our initial thinking , First, parallel the serial time of two subtrees , That is, serial time a and c Parallel execution , So one of them 2 Time becomes parallel time , And then there were 1 Time we try to use 1 The parallel execution time of the right subtree of . How to consume ？ It's equivalent that we can't hold the same thing in both hands , There are now three categories of objects , The first and second categories each have 4kg, The third category of goods is 1kg, If we start taking 1,2 Such items , Time consuming 4 Take it , after 1 Time holds the third kind of objects in one hand ; If you take half first 3 And as many 1, Take the other half 3 And as many 2, such 3 The items are finished , There are only two items left 3.5kg 了 , Keep holding it with both hands , The change of the order of taking the items made our hands not rest in the whole process , Reduced execution time .

Summarize the idea of this topic , In the root A tree for roots , Let the serial time of the left subtree task execution be a, Parallel time is b; The serial time of the right subtree is c, Parallel time is d. Might as well set a > c, In order to minimize the task execution time , We're going to put c The serial time of is used for a and c parallel , The rest a - c Parallel time for serial time attempts d Consumed , That is to say, the serial time and parallel time of the right subtree are used to consume the serial time of the left subtree , Why not use the parallel time consumption of the left subtree ？ Because what we get a and b It is already the minimum serial and parallel time of the left subtree , There is no way to reduce the serial time from the left subtree itself .d How much can be consumed a -c The serial time ？

We use use cases 1 For example

We get it recursively 47 The serial time of the left subtree of a = 74, Parallel time b = 0; Right subtree serial time c = 31, Parallel time d = 0. According to the above theory , First use the right subtree serial time 31 To consume the serial time of the left subtree , Increased the parallel time of the whole tree 31. At this time, the left subtree is left 43 Serial time , But because the parallel time of right subtree is 0, There is no task to be associated with 74 The task continues to be executed in parallel , So the serial time cannot be reduced any more . If 31 Add two 15 The child node of time , So the right child's parallel time d = 15 了 , We use first 15 Time to execute 74 Task and a 15 Mission ; Reuse 15 Time to execute 74 Task and another 15 Mission , So one to two parallel 15 After the task is completed 74 The serial time is reduced 30,43 - 30 = 13,d = 15 When is 74 Again, it reduces 30 Serial time ; If the parallel time of the right subtree is d = 21.5 Well , Well, the two one. 21.5 The tasks of go and 74 Tasks are executed in parallel , Just enough to consume the rest 43 Serial time . If d Continue to increase , For example, add to 30, We still can only use 21.5 Time turns and 74 The task parallel ,74 After the task is executed, there is no serial task , The remaining parallel tasks of the right subtree continue . According to this example, we can draw a conclusion that , Serial time of left subtree a Among them c Time is the serial time of the right subtree c Consumed , The rest a -c We can try to use the parallel time of the right subtree d Consumed .

If a - c <= 2 * d, Then the two execution times are d Tasks can be consumed in turn a - c Serial time ;
If a - c > 2 * d, Then the two execution times are d Your task can only consume 2d Serial time .

The idea of solving the problem is obvious , Recursively find out root The string of left and right subtrees 、 Parallel time ab and cd, If c > a Just exchange a and c、b and d, Ensure that the serial time of the lower left subtree is large . Then ask for root Is the serial time and parallel time of the root tree , The serial time must be added first root Its own execution time root->val, Then add left 、 Serial time of right subtree , hypothesis d The serial time that can consume the left subtree is t, add c Serial time consumed c, Then the remaining serial time of the left and right subtrees is a - c - t. The parallel time is equal to the parallel time of the original left and right subtrees b + d, Add the original c Parallel time converted from serial time , Plus with d The serial time of the left subtree consumed t / 2, Why? t Divide by 2？ go back to a - c = 1,d = 4 This example of , If two cores can perform the same task , So serial time 1 Just execute in parallel 0.5 That's it . The result of changing the execution order is equivalent to parallel execution a -c For this task ,0.5 Time execution 4 and 1, 0.5 Time to execute another 4 and 1, Consume 1 Time , The rest 3.5 Time to complete two 4 The rest , This parallel time is equal to 4.5, Compared with the original d = 4 The increase happens to be 0.5. So when the serial task is executed in parallel , The increased parallel time is naturally equal to the serial time / 2.

Last , The execution time of the entire tree is equal to the serial time + Parallel time .

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    pair<int,double> dfs(TreeNode* root){
        if(!root)   return {0,0};
        auto x = dfs(root->left);
        auto y = dfs(root->right);
        if(x.first < y.first)   swap(x,y);
        int a_c = x.first - y.first;// Subtract the serial time after serial parallelism 
        int t = a_c;// The remaining serial time can be used for parallel time 
        if(t > 2 * y.second)    t = 2 * y.second;
        int a = root->val + a_c - t;
        double b = x.second + y.second + y.first + t / 2.0;
        return {a,b};
    }
    double minimalExecTime(TreeNode* root) {
        auto res = dfs(root);
        return res.first + res.second;
    }
};