当前位置:网站首页>Maximum sum and promotion of continuous subarrays (2)
Maximum sum and promotion of continuous subarrays (2)
2022-07-24 18:14:00 【Xiao Liu xuezhuo】
Knowledge point greedy Dynamic programming Array Double pointer
describe
Enter a length of n Integer array array, One or more consecutive integers in an array form a subarray , Find a continuous subarray with the largest sum .
1. Subarray is continuous , such as [1,3,5,7,9] The subarrays of are [1,3],[3,5,7] wait , however [1,3,7] It's not a subarray
2. If there are multiple consecutive subarrays with the largest sum , Then return the longest , The data of this question ensure that there is only one
3. The minimum length of the subarray defined by this question is 1, There is no empty subarray , That there is no [] Is a sub array of an array
4. The returned array is not included in the space complexity calculation
Data range :
1<=n<=10^51<=n<=105
-100 <= a[i] <= 100−100<=a[i]<=100
requirement : Time complexity O(n)O(n), Spatial complexity O(n)O(n)
Advanced : Time complexity O(n)O(n), Spatial complexity O(1)O(1)

The maximum sum of continuous subarrays has been done before , But this problem is more difficult , If there are multiple consecutive subarrays with the largest sum , Ask for the longest . The title ensures that the longest result of the input array is only one .
To analyze this problem , We have used the idea of dynamic programming to calculate the maximum sum of continuous subarrays . Now you also need to attach the length information of the maximum array . When we count the maximum , You also need to count the subscript of the first element and the subscript of the last element of the continuous subarray of the maximum , In this way, we can pick out the subarray we want from the array , Instead of simply picking out the sum of all elements of the largest continuous subarray .
Suppose we have two variables max_start and max_end Represents the starting and ending subscripts of the largest and longest continuous subarray respectively . We need to consider how to assign initial values to these two values and where to dynamically adjust these two values in the program .
Let's see how the algorithm of maximum sum of continuous subarrays is implemented , Then think about where you can dynamically adjust max_start and max_end.
public int FindGreatestSumOfSubArray(int[] array) {
int length = array.length;
int add = array[0]; // Used to save traversal to i~index Maximum value of contiguous subarray at interval
int max = array[0]; // Used to save the maximum value
for (int i = 1; i < length; i++) {
if (add > 0) {
add = add + array[i];
} else {
add = array[i];
}
if (add > max) {
max = add;
}
}
return max;
}First , Out of the loop max=array[0], therefore max_start and max_end Should be initialized to array[0] The subscript . namely max_start=0,max_end=0;
Then it's easy to think , You can find something better than the current max Larger values are given max At the same time of assigning new value , Also give max_start and max_end Assign new values to .
Then the code becomes as follows .
public int FindGreatestSumOfSubArray(int[] array) {
int length = array.length;
int add = array[0]; // Used to save traversal to i~index Maximum value of contiguous subarray at interval
int max = array[0]; // Used to save the maximum value
int max_start = 0; // Used to record max From
int max_end = 0; // Used to record max The ending coordinate of
for (int i = 1; i < length; i++) {
if (add > 0) {
add = add + array[i];
} else {
add = array[i];
}
if (add > max) {
max = add;
max_start = xxx1;
max_end = xxx2;
}
}
int [] B = new int [max_end - max_start + 1];
for (int i = max_start, j = 0; i <= max_end; i++, j++) {
B[j] = array[i];
}
return B;
}At this time, we found out where to adjust dynamically max_start and max_end. But at present, it is uncertain what value it should be assigned , Further analysis is needed .
Because it is add > max Make the above changes when , add Represents the maximum sum of successive subarrays with the currently traversed element as the tail element , The subscript of the first element is also dynamic . To put it bluntly add It also points to a continuous sub array , When add The ratio of continuous sub arrays pointed to max When the sum of all elements of the continuous subarray pointed to is larger , use add Replace max, Simultaneous use add Replace the leading and trailing subscripts of max Leading and trailing subscripts of . So the problem turns into solving add The beginning and end of the array are subscripted . add The subscript of the tail element of is the current traversal position , namely index. What about the subscript of the first element ? Current programs do not have a variable store add Subscript value of the first element , So we also need to use a variable to dynamically adjust in the appropriate position of the program add Subscript value of the first element .
After adjustment, the program representative becomes
public int FindGreatestSumOfSubArray(int[] array) {
int length = array.length;
int add = array[0]; // Used to save traversal to i~index Maximum value of contiguous subarray at interval
int max = array[0]; // Used to save the maximum value
int max_start = 0; // Used to record max From
int max_end = 0; // Used to record max The ending coordinate of
int add_start= 0; // Tag traverses to i Location , With i Is the subscript of the first number of the maximum sum of the contiguous subarrays at the end
for (int i = 1; i < length; i++) {
if (add > 0) {
add = add + array[i];
} else {
add = array[i];
add_start= i;
}
if (add > max) {
max = add;
max_start = xxx1;
max_end = xxx2;
}
}
int [] B = new int [max_end - max_start + 1];
for (int i = max_start, j = 0; i <= max_end; i++, j++) {
B[j] = array[i];
}
return B;
}You can see , Variable add_start Used to represent add The subscript value of the first element of the continuous subarray pointed to , I chose to be in add<0 When , Dynamic adjustment is needed add When , Also incidentally adjusted add_start Value .
Now add The subscript values of the first and last elements of have been found , Directly replace the above xxx1 and xxx2 that will do .
public int FindGreatestSumOfSubArray(int[] array) {
int length = array.length;
int add = array[0]; // Used to save traversal to i~index Maximum value of contiguous subarray at interval
int max = array[0]; // Used to save the maximum value
int max_start = 0; // Used to record max From
int max_end = 0; // Used to record max The ending coordinate of
int add_start= 0; // Tag traverses to i Location , With i Is the subscript of the first number of the maximum sum of the contiguous subarrays at the end
for (int i = 1; i < length; i++) {
if (add > 0) {
add = add + array[i];
} else {
add = array[i];
add_start= i;
}
if (add > max) {
max = add;
max_start = add_start;
max_end = i;
}
}
int [] B = new int [max_end - max_start + 1];
for (int i = max_start, j = 0; i <= max_end; i++, j++) {
B[j] = array[i];
}
return B;
}Come here , The general framework of the algorithm is all out . But don't forget , The title requires the largest and longest continuous subarray . So we need to deal with the maximum max There are many situations .
public int FindGreatestSumOfSubArray(int[] array) {
int length = array.length;
int add = array[0]; // Used to save traversal to i~index Maximum value of contiguous subarray at interval
int max = array[0]; // Used to save the maximum value
int max_start = 0; // Used to record max From
int max_end = 0; // Used to record max The ending coordinate of
int add_start= 0; // Tag traverses to i Location , With i Is the subscript of the first number of the maximum sum of the contiguous subarrays at the end
for (int i = 1; i < length; i++) {
if (add > 0) {
add = add + array[i];
} else {
add = array[i];
add_start= i;
}
if (add > max) {
max = add;
max_start = add_start;
max_end = i;
} else if (add == max) {
if ((i - add_start) > (max_end - max_start)) {
max_start = add_start;
max_end = i;
}
}
}
int [] B = new int [max_end - max_start + 1];
for (int i = max_start, j = 0; i <= max_end; i++, j++) {
B[j] = array[i];
}
return B;
}It deals with max Equal values .
Last little note : Because it requires the largest and longest continuous subarray , The algorithm is dealing with add Of , When add<=0 Will be reset when add The value of and add_start Value . This is actually inappropriate . Because what we need now is the longest continuous subarray , So we should add=0 It's only right to include this part of . Just put the top ”add > 0“ Change to “add >= 0” that will do .
So the final complete algorithm code is :
public int FindGreatestSumOfSubArray(int[] array) {
int length = array.length;
int add = array[0]; // Used to save traversal to i~index Maximum value of contiguous subarray at interval
int max = array[0]; // Used to save the maximum value
int max_start = 0; // Used to record max From
int max_end = 0; // Used to record max The ending coordinate of
int add_start= 0; // Tag traverses to i Location , With i Is the subscript of the first number of the maximum sum of the contiguous subarrays at the end
for (int i = 1; i < length; i++) {
if (add >= 0) {
add = add + array[i];
} else {
add = array[i];
add_start= i;
}
if (add > max) {
max = add;
max_start = add_start;
max_end = i;
} else if (add == max) {
if ((i - add_start) > (max_end - max_start)) {
max_start = add_start;
max_end = i;
}
}
}
int [] B = new int [max_end - max_start + 1];
for (int i = max_start, j = 0; i <= max_end; i++, j++) {
B[j] = array[i];
}
return B;
}边栏推荐
猜你喜欢

Inheritance and Derive
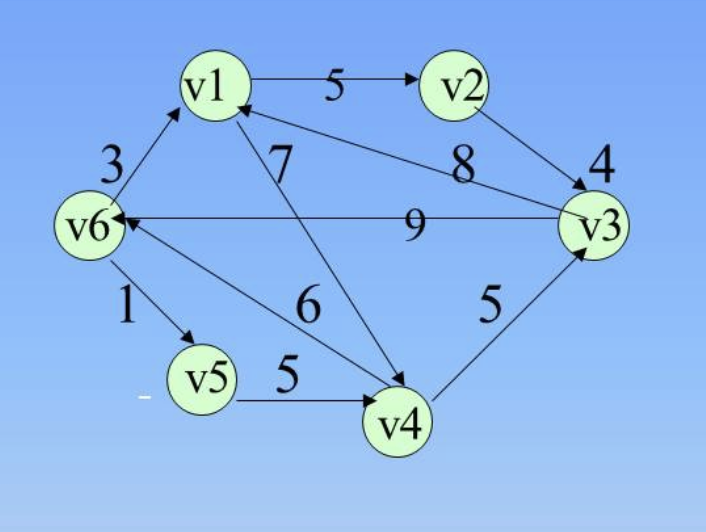
Definition and storage of adjacency table and adjacency storage of directed graph and undirected graph

jmeter --静默运行
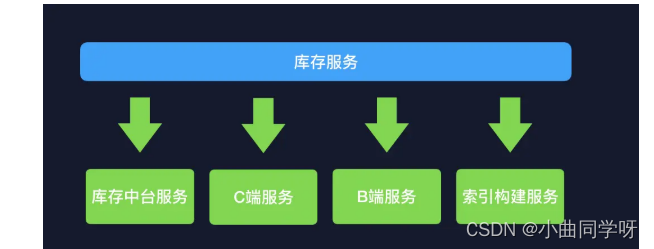
What are the pitfalls from single architecture to distributed architecture?

Use prometheus+grafana to monitor MySQL performance indicators
![[OBS] dependency Library: x264 vs Build](/img/24/4caea5dc6ff092a3161f43b6026d25.png)
[OBS] dependency Library: x264 vs Build

Laravel notes - RSA encryption of user login password (improve system security)

6126. 设计食物评分系统
去不图床容量兑换

如何用WebGPU流畅渲染百万级2D物体?
随机推荐
How to render millions of 2D objects smoothly with webgpu?
Still building projects from scratch? This upgraded rapid development scaffold is worth a try!
pinia 入门及使用
【obs】视频、音频编码与rtmp发送的配合
Common methods of string (2)
JMeter -- silent operation
继承与派生
redis集群的三种方式
1688/ Alibaba searches new product data by keyword API instructions
2022 the latest short video de watermarking analysis API interface sharing
odoo中的bom理解
Blackmagic Fusion Studio 18
2022最新短视频去水印解析API接口分享
[OBS] dependency Library: x264 vs Build
0613 ~ self study
How to prepare for hyperinflation
How to read "STL source code analysis"?
手写博客平台~第二天
如何向 google colab 快速上传文件
Simple test JS code