Prim minimum spanning tree (diagram)

What is a spanning tree

Subgraphs ：G=<V,E>,G'=<V', E'>, For two pictures （V For point set , That is, the set of points in the graph ,E Set for the side ）, If V' yes V And E' yes E Subset , be G' yes G The children of .

If V'=V, said G' by G The generated subgraph

If G' It is an undirected subgraph and is the structure of a tree , Is the spanning tree

Minimum spanning tree

Minimum spanning tree ： It's a card with the right to Undirected connectivity The minimum spanning tree of the sum of edge weights in a graph

Prim Algorithm ：

Maintain a set of points that have been added to the minimum spanning tree C, Connect a point set that is not at this point through one edge at a time C The point of , Until it finally forms a tree structure

Dist(u) Express u Point to point set C The minimum distance of the point in

Select one point set at a time C distance Minimum Add points to the point set C, And update the point-to-point set not added through the added points C The minimum distance （ because C An additional point has been added to the ）, until n Add all points to the point set C Or no point can join （ Cannot form a connected graph ）.

The illustration

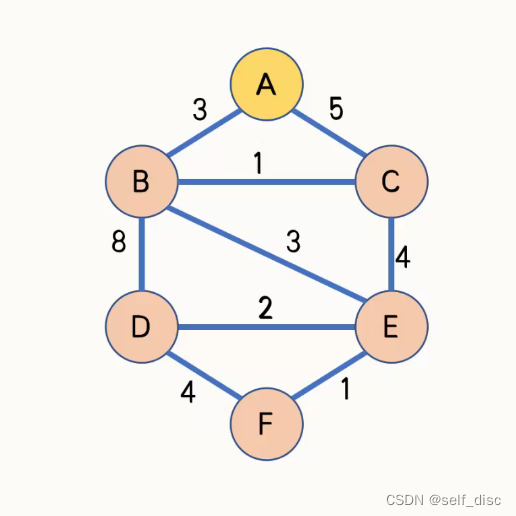
Preface ： Has been added to the point set C The dots are marked in blue , The currently added points are marked in red , Updated by the currently added point dist Marked in red .

initial ： Add an initial point A, And pass A to update dist

u	A	B	C	D	E	F
dist(u)	0	3	5	inf	inf	inf

Add the second point B：B To the point set C The distance is the smallest , And pass B to update dist

u	A	B	C	D	E	F
dist(u)	0	3	1	8	3	inf

Add the third point C：C To the point set C The distance is the smallest , And pass C to update dist

u	A	B	C	D	E	F
dist(u)	0	3	1	8	3	inf

Add the fourth point E：E To the point set C The distance is the smallest , And pass E to update dist

u	A	B	C	D	E	F
dist(u)	0	3	1	2	3	1

  Add the fifth point F：F To the point set C The distance is the smallest , And pass F to update dist

u	A	B	C	D	E	F
dist(u)	0	3	1	2	3	1

  Add the sixth point D：D To the point set C The distance is the smallest , And pass D to update dist

u	A	B	C	D	E	F
dist(u)	0	3	1	2	3	1

  Add all points to the point set ,Prim The algorithm ends .

Complexity analysis ：

A total of n A little bit , Every time you need to traverse dist Find the minimum value of the array , And update the points that are not added to the point set through this point dist value , That is, enumerate the edges connected by the point to update the corresponding dist, So the complexity is ：

        O（n*n）+    = O（n*n + m）（mi The number of edges connected for each point , The sum is the total number of sides ）

Pseudo code ：

 int prim()

{

    memset(dis, 127, sizeof(dis)); // The initial setting is positive infinity

    memset(vis, 0, sizeof(vis));   // The initial set points are not in the point set , The point set is empty

    ans = 0, cnt = 0;              // The initial weight is 0

    dis[1] = 0;                    // 1 Add point set

    while (1)

    {

        int u = -1;

        for (int i = 1; i <= n; i++)

        {

            if (vis[i] == 0 && dis[i] < (1 << 30)) // i The points are not in the point set and are connected to the points in the point set

            {

                if (u == -1 || dis[i] < dis[u]) // u==-1 -> The first point can be updated to the nearest point in the point set

                {

                    u = i; // Update the latest point

                }

            }

        }

        if (u == -1)

            break;            // If you can't find the point added to the point set , Then end the algorithm

        cnt++, ans += dis[u]; // Number of points in the point set +1,ans add u Join the edge weight of the point set

        vis[u] = true;        // vis Add point set

        for (auto it : a[u])//a[u] For u A collection of points of connected edges ,v For connected points ,w For border power

        {

            dis[it.v] = min(dis[it.v], it.w); // Pass the point v The connected edge updates the point that is not in the point set dist value

        }

    }

    if (cnt == n)

        return ans; // Be able to join n Points form a connected graph , The spanning tree returns the weight

    else

        return -1; // Cannot form a spanning tree

}

The template questions  

Topic link ： Minimum spanning tree 1 - subject - Daimayuan Online Judge

Title Description ：

Give you a simple undirected connected graph , Edge weights are nonnegative integers . You need to find its minimum spanning tree , Just output the weight sum of the edges .

The figure is given in the following form ：

Enter two integers on the first line  n,m, Represents the number of vertices of a graph 、 Number of edges , Vertex number from  1  To  n.

Next  m  That's ok , Three integers per row  x,y,z Express  x  And  y  There is a side between , The boundary right is  z.

Input format ：

The first line has two integers  n,m.

Next  m  That's ok , There are three integers on each line , Represents an edge .

Output format ：

Output a number , Represents the weight sum of the minimum spanning tree .

Data scale ：

For all the data , Guarantee  2≤n≤1000,n−1≤m≤100000,1≤x,y≤n,x≠y,1≤z≤10000

The sample input ：

4 4

1 2 1

2 3 3

3 4 1

1 4 2

Sample output ：

4 

  See the code for details. ：

#include <bits/stdc++.h>
using namespace std;
int dis[100009], cnt, ans, n, m; // dis Is the minimum distance from point to point set ,cnt Is the number of points in the point set ,ans For the current edge weight and 
bool vis[100009];
struct node
{
    int v, w;
};
vector<node> a[100009]; // Save map 
int prim()
{
    memset(dis, 127, sizeof(dis)); // The initial setting is positive infinity 
    memset(vis, 0, sizeof(vis));   // The initial set points are not in the point set , The point set is empty 
    ans = 0, cnt = 0;              // The initial weight is 0
    dis[1] = 0;                    // 1 Add point set 
    while (1)
    {
        int u = -1;
        for (int i = 1; i <= n; i++) // Traverse to find the point with the minimum distance not added to the point set 
        {
            if (vis[i] == 0 && dis[i] < (1 << 30)) // i The points are not in the point set and are connected to the points in the point set 
            {
                if (u == -1 || dis[i] < dis[u]) // u==-1 -> The first point can be updated to the nearest point in the point set 
                {
                    u = i; // Update the latest point 
                }
            }
        }
        if (u == -1)
            break;            // If you can't find the point added to the point set , Then end the algorithm 
        cnt++, ans += dis[u]; // Number of points in the point set +1,ans add u Join the edge weight of the point set 
        vis[u] = true;        // vis Add point set 
        for (auto it : a[u])
        {
            dis[it.v] = min(dis[it.v], it.w); // Pass the point v The connected edge updates the point that is not in the point set dist value 
        }
    }
    if (cnt == n)
        return ans; // Be able to join n Points form a connected graph , The spanning tree returns the weight 
    else
        return -1; // Cannot form a spanning tree 
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        int u, v, w;
        cin >> u >> v >> w;
        node t1, t2; // An undirected graph has edges 
        t1.v = v, t1.w = w;
        a[u].push_back(t1); // u->v  The boundary right is w
        t2.v = u, t2.w = w;
        a[v].push_back(t2); // v->u  The boundary right is w
    }
    cout << prim();
}

  reference ：

2022 Namomo Spring Camp Div2 Day10  Live class

ending

If there are any mistakes, please correct them ！ Thank you for ！