当前位置:网站首页>概率论基础 - 15 - 伽马分布
概率论基础 - 15 - 伽马分布
2022-08-05 14:30:00 【为为为什么】
本文记录伽马分布。
整数次数的伽马分布
若事件服从泊松分布,泊松分布参数为\lambda,则事件第i 次发生和第i+k 次发生的时间间隔t的分布为伽玛分布。
概率密度函数
其中 t 为时间间隔。
期望
方差
上面的定义中 k 必须是整数。
更一般的伽马分布
- 事实上,若随机变量 X 服从伽马分布,则其概率密度函数为:
期望
方差
当 \alpha \leq 1 时, p(X ; \alpha, \beta) 为递减函数。 当 \alpha>1 p(X ; \alpha, \beta) 为单峰函数。
整数次数伽马分布的理解
- 已知Gamma分布的密度函数为:
- 则其在时间 (t,+\infty) 上的积分为
- 即有:
- 令 \alpha 为 n, \quad n=0,1,2, \cdots , 有
- 叠加求和, 得:
Gamma分布上述积分形式即可理解为: 第 n 个事件恰好发生在时间 (t,+\infty) 的概率, 相当于 在时间 (0, t) 内发生恰好发生 0,1,2, \cdots, n-1 个事件的概率总和。
也可以反过来说,伽马分布是n个独立的指数分布随机变量的和。
伽马函数
伽玛函数(Gamma Function)作为阶乘的延拓,是定义在复数范围内的亚纯函数,通常写成 \Gamma(x) 。 在x取值为正整数时与阶乘是统一的。
- 在实数域上伽玛函数定义为:
- 在复数域上伽玛函数定义为:
其中 \operatorname{Re}(z)>0
- 除了以上定义之外,伽马函数公式还有另外一个写法:
我们都知道 \int_{0}^{+\infty} e{-t{2}} \mathrm{~d} t=\frac{\sqrt{\pi}}{2} 是一个常用积分结果 上述公式可以用 \Gamma\left(\frac{1}{2}\right)=2 \int_{0}^{\perp \infty} e{-t{2}} \mathrm{~d} t=\sqrt{\pi} 来验证
- 伽马函数还可以定义为无穷乘积:
参考资料
边栏推荐
猜你喜欢
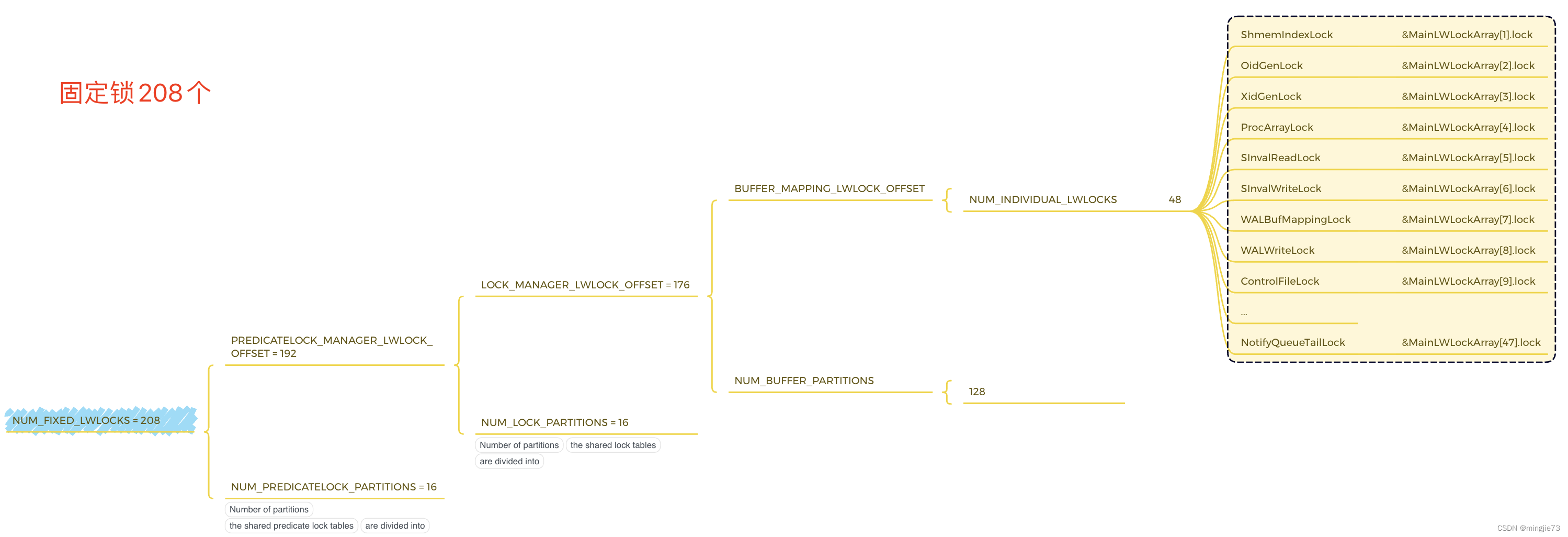
Postgresql源码(67)LWLock锁的内存结构与初始化

期货开户公司的选择和作用

NLP paper reading | Parametric machine translation meets comparative learning: I want both efficiency and performance!

2022最新综述 | 面向大规模场景的小目标检测:综述和 benchmark

HDD杭州站•ArkUI让开发更灵活

Redis-浅谈主从同步

Use Redis source code to compile and release Redis For Windows distribution package for Windows

shell实现加密压缩文件自动解压

内存问题难定位,那是因为你没用ASAN
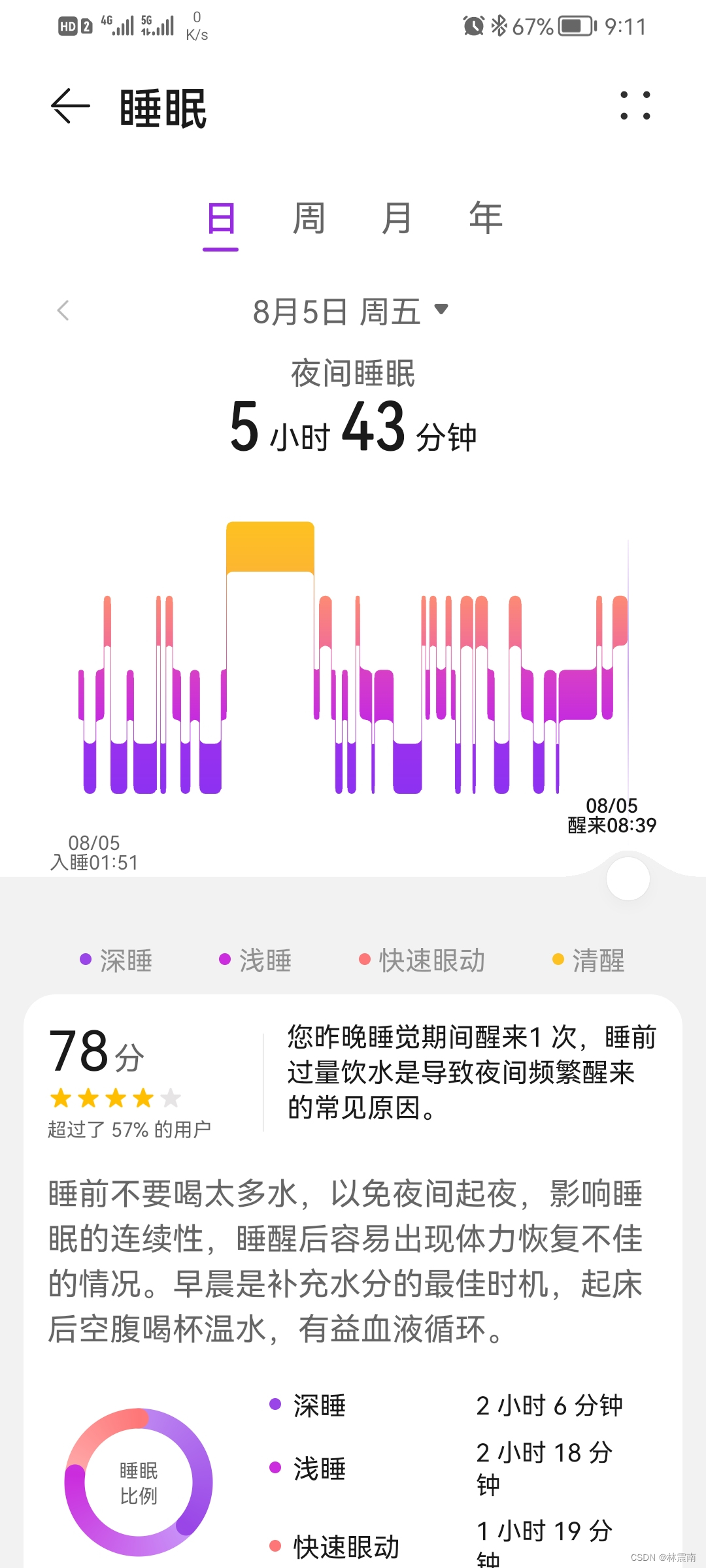
Today's sleep quality record 78 points
随机推荐
Kernel implementation of buddy allocator
ByteDance Flink Status Query Practice and Optimization
DevEco Studio配置:自定义头部代码注释
双因子与多因子身份验证有什么区别?
Design of Fingerprint Time Attendance Machine + Host Computer Management Based on STM32 MCU
DevEco Studio Configuration: Custom Header Code Comments
sklearn Notes: PCA
PaddleOCR使用指南
深度学习之 11 空洞卷积的实现
Feign 的简单使用
目前民生期货这家期货公司怎么样?安全吗?
2022-08-02~04 第四小组 修身课 学习笔记(every day)
OpenHarmony Pixel Unit (eTS)
Postgresql源码(67)LWLock锁的内存结构与初始化
mmap kernel implementation and physical memory organization
抖音自媒体运营的5个技巧,让你的账号快速涨粉
shell实现加密压缩文件自动解压
OpenHarmony如何查询设备类型
响应式织梦模板花店鲜花类网站
d rebinding unchanged