当前位置:网站首页>Special lecture 5 combinatorial mathematics learning experience (long-term update)
Special lecture 5 combinatorial mathematics learning experience (long-term update)
2022-07-23 13:38:00 【Fanshui 682】
Post a website :
ZJNU-2022 Summer topics - Combinatorial mathematics - Virtual Judge (vjudge.net)
Self closing knowledge posted by senior students
Catalog
The formula for finding the most cost-effective inverse element

Knowledge point :
The formula for finding the most cost-effective inverse element
First find the tail inv, Then go back layer by layer .
rep(i,2,N-5){
f[i]=f[i-1]*i%p;
}
inv[N-5]=fastpower(f[N-5],p-2,p);
nep(i,N-6,2){
inv[i]=inv[i+1]*(i+1)%p;
}Dislocation
// Staggered recurrence formula
d[1]=0;d[2]=1;d[3]=2;
//d It means all wrong rows n How many are there
rep(i,4,N){
d[i]=((i-1)*(d[i-1]+d[i-2]))%p;
}
// so 5 A wrong number 3 individual , Namely C(3,5)*d[3];Lucas
// Find combination , When q Ask the remainder of times p(<1e6 And prime number ) Use when the value of will change .
int lucas(int n,int m){
if (!m) return 1;
return c(n%p,m%p)*lucas(n/p,m/p)%p;
}Example :
E - Shinyruo and KFC
Carelessness :n A food , Every food ai individual ,m A team , Each team can eat at most one of each kind of food , Ask the teams to be 1~m When , Distribute different situations when food is finished .
The senior said it was a bronze medal problem .
This problem also has a problem surface , Is that all ai And not more than 1e5, and n It's also 1e5, So different ai Only up to sqrt(1e5) individual , So the drawer principle , There will be a lot of repetition , This is the time unordered_map Put into , Time complexity becomes ,n*sqrt(1e5)* Fast power logn, It's over .
summary : Bronze medal questions pay more attention to the processing of data of different topics .
#include <bits/stdc++.h>
#define rep(i,l,r) for (int i=l;i<=r;i++)
#define nep(i,r,l) for (int i=r;i>=l;i--)
#define pii pair<int,int>
#define int long long
#define CIO std::ios::sync_with_stdio(false)
using namespace std;
const int N=2e5+5;
const int p=998244353;
int a[N],t[N],tn[N];
int f[N],inv[N],finv[N];
unordered_map <int,int> mp;
int fastpower(int a,int x,int p){
int ans=1;
while (x){
if (x&1) ans=(ans*a)%p;
x=x/2;
a=(a*a)%p;
}
return ans%p;
}
void Int(){
f[0]=inv[0]=f[1]=inv[1]=finv[0]=finv[1]=1;
rep(i,2,N-5){
f[i]=f[i-1]*i%p;
}
inv[N-5]=fastpower(f[N-5],p-2,p);
nep(i,N-6,2){
inv[i]=inv[i+1]*(i+1)%p;
}
}
int c(int m,int n){
if (m>n) return 0;
return f[n]*inv[n-m]%p*inv[m]%p;
}
void work(){
Int();
int n,m;cin>>n>>m;
int ma=0;
rep(i,1,n){
cin>>a[i];
mp[a[i]]++;
ma=max(ma,a[i]);
}
int ans=0;
unordered_map<int,int>::iterator it;
int cnt=0;
for(it=mp.begin();it!=mp.end();it++){
t[++cnt]=it->second;
tn[cnt]=it->first;
}
rep(i,1,m){
if (i<ma) cout<<0<<endl;
else{
ans=1;
rep(j,1,cnt){
if (t[j]!=0){
int zhi=fastpower(c(tn[j],i),t[j],p);
if (zhi!=0){
ans=ans*zhi%p;
}
}
}
cout<<ans<<endl;
}
}
}
signed main(){
CIO;
work();
return 0;
}
G - Coin shopping
share 4 Grow coins . The denominations are c1,c2,c3,c4.
Someone goes to the store to buy something , Went to the n Time , For every purchase , He brought di gold i Grow coins , Want to buy s The value of things . How many payment methods are there at a time .
This is a way dp+ An inclusive problem , If there is no quantitative limit , It's a board problem of complete knapsack , Let's assume that one exceeds the limit , The other is a complete backpack , Then suppose four times , Finally, subtract , But I find that I will lose more , This is the principle of inclusion and exclusion , Then continue processing , violence +- Just fine , Only 4 Grow coins .
#include <bits/stdc++.h>
#define rep(i,l,r) for (int i=l;i<=r;i++)
#define nep(i,r,l) for (int i=r;i>=l;i--)
#define pii pair<int,int>
#define int long long
#define CIO std::ios::sync_with_stdio(false)
using namespace std;
const int N=2e5+5;
const int p=998244353;
int c[10],dp[N];
int d[10],s;
int sum(int idx){
return c[idx]*(d[idx]+1);
}
void work(){
int n;
rep(i,1,4){
cin>>c[i];
}
dp[0]=1;
rep(i,1,4){
for (int j=c[i];j<N;j++){
dp[j]+=dp[j-c[i]];
}
}
cin>>n;
rep(i,1,n){
rep(j,1,4){
cin>>d[j];
}
cin>>s;
int ans=dp[s];
if (s>=sum(1)) ans-=dp[s-sum(1)];
if (s>=sum(2)) ans-=dp[s-sum(2)];
if (s>=sum(3)) ans-=dp[s-sum(3)];
if (s>=sum(4)) ans-=dp[s-sum(4)];
if (s>=sum(1)+sum(2)) ans+=dp[s-sum(1)-sum(2)];
if (s>=sum(1)+sum(3)) ans+=dp[s-sum(1)-sum(3)];
if (s>=sum(1)+sum(4)) ans+=dp[s-sum(1)-sum(4)];
if (s>=sum(2)+sum(3)) ans+=dp[s-sum(2)-sum(3)];
if (s>=sum(2)+sum(4)) ans+=dp[s-sum(2)-sum(4)];
if (s>=sum(3)+sum(4)) ans+=dp[s-sum(3)-sum(4)];
if (s>=sum(1)+sum(2)+sum(3)) ans-=dp[s-sum(1)-sum(2)-sum(3)];
if (s>=sum(1)+sum(3)+sum(4)) ans-=dp[s-sum(1)-sum(3)-sum(4)];
if (s>=sum(1)+sum(2)+sum(4)) ans-=dp[s-sum(1)-sum(2)-sum(4)];
if (s>=sum(2)+sum(3)+sum(4)) ans-=dp[s-sum(2)-sum(3)-sum(4)];
if (s>=sum(1)+sum(2)+sum(3)+sum(4)) ans+=dp[s-sum(1)-sum(2)-sum(3)-sum(4)];
cout<<ans<<endl;
}
}
signed main(){
CIO;
work();
return 0;
}
边栏推荐
- Opencv video operation
- Knowledge map: basic concepts
- QNX修改系统时间
- Opencv image processing (medium) image smoothing + histogram
- 在虚拟环境下使用pip时默认使用系统环境的pip该怎么办
- Shooting lesson 1-3: image Sprite
- 专题讲座5 组合数学 学习心得(长期更新)
- 学会用canvas构建折线图、柱状图、饼状图
- Point target simulation of SAR imaging (I) -- mathematical model
- Beifu PLC and C transmit int array type variables through ads communication
猜你喜欢
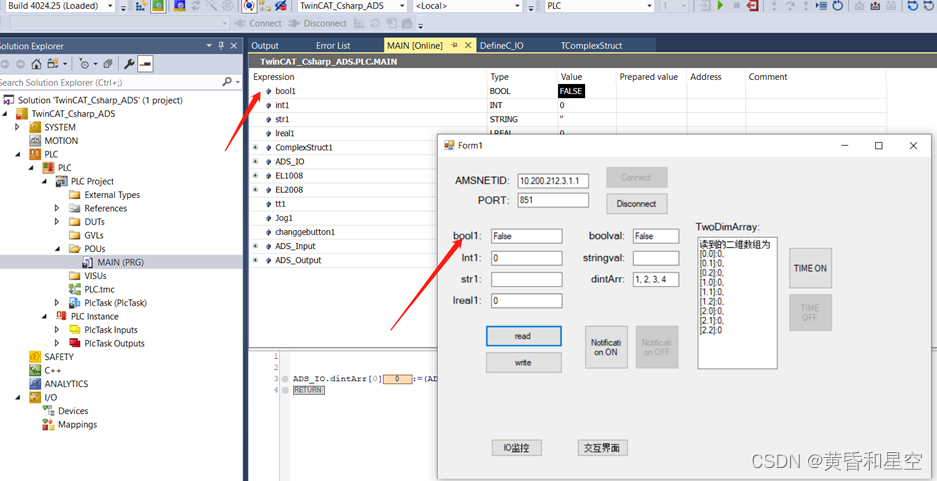
倍福PLC和C#通过ADS通信传输bool类型变量
![[jzof] path in matrix 12](/img/33/426386fc3dc3e32b6968d30034d66a.png)
[jzof] path in matrix 12

Machine learning, Wu Enda, logical regression

基于BIM+3DGIS的智慧城市基础设施管理
![[noi simulation race] I don't know which CF paper title it is (probability expectation, martingale's stop time theorem)](/img/79/46e9bf2b39fbec9ae913c4e205acdc.png)
[noi simulation race] I don't know which CF paper title it is (probability expectation, martingale's stop time theorem)

Hardware system architecture of 4D millimeter wave radar

0722~ thread pool extension

ES6——周考题

Beifu PLC and C transmit string array type variables through ads communication

Beifu PLC -- C ads communication reads variables in the form of notification
随机推荐
倍福PLC和C#通过ADS通信传输String数组类型变量
Outlook tutorial, how to switch calendar views and create meetings in outlook?
Shell运算符、$((运算式))” 或 “$[运算式]、expr方法、条件判断、test condition、[ condition ]、两个整数之间比较、按照文件权限进行判断、按照文件类型进行判断
Special topic of MIMO Radar (0) - General Chapter
Uncaught (in promise) Neo4jError: WebSocket connection failure. Due to security constraints in your
ES6——周考题
【可視化調度軟件】上海道寧為SMB組織帶來NETRONIC下載、試用、教程
【可视化调度软件】上海道宁为SMB组织带来NETRONIC下载、试用、教程
Space shooting part 2-2: enemy spirit
【深入浅出玩转FPGA学习10------简单的Testbench设计】
Jenkins continuous integration error stderr: fatal: unsafe repository ('/home/water/water' is owned by someone else)
Point target simulation of SAR imaging (I) -- mathematical model
Beifu PLC -- C ads communication reads variables in the form of notification
我为大厂怒刷的《100道Android面试题》
Space shooting part 1: player spirit and control
第十一天笔记
学会用canvas构建折线图、柱状图、饼状图
2022-07-22 回顾链表操作以及部分问题
Wu Enda machine learning series p31~p42
Power BI----综合应用