【图论】—— 二分图

---

如果一张无向图的 N 个结点 可以分成 A,B 两个非空集合，其中 ，并且在同一集合内的点之间都没有边相连，那么称这张无向图为一张二分图。A.B分别称为二分图的左部和右部。

---

二分图的判定

定理：

一张图是二分图，当且仅当图中不存在奇数环（长度是奇数的环）。

染色法判二分图

根据上述的定理，我们可以用染色法进行二分图判定。

大致思想为：尝试用黑白两种颜色标记图中的节点，当一个节点被标记后，它的所有相邻节点应被标记为与它相反的颜色。若标记过程产生冲突，则说明图中存在奇环。

二分图一般基于深度优先遍历，时间复杂度为 

代码实现

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 100010, M = N * 2;

int n, m;
int h[N], ne[M], e[M], idx;
int color[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

bool dfs(int u,int c)
{
    color[u] = c;

    for(int i = h[u];i != -1;i = ne[i])
    {
        int j = e[i];
        if(!color[j]) 
        {
            if(!dfs(j,3 - c)) return false;
        }
        else if(color[j] == c) return false;
    }

    return true;
}

int main()
{
    cin >> n >> m;
    
    memset(h, -1, sizeof h);
    
    while(m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }
    
    bool flag = true;
    for(int i = 1; i <= n; i ++ )
        if(!color[i])
        {
            if(!dfs(i, 1))
            {
                flag = false;
                break;
            }
        }
    
    if(flag) puts("Yes");
    else puts("No");
    
    return 0;
}

---

 二分图最大匹配

“任意两条边都没有公共端点”的边的集合被称为图的一组匹配。

在二分图中，包含边数最多的一组匹配被称为二分图的最大匹配。

对于任意的一组匹配 S（S 是一个边集），属于 S 的边被称为“匹配边”，不属于 S 的边称为“非匹配边”。匹配边的端点称为“匹配点”，其他节点被称为“非匹配点”。

如果二分图中存在一条连接两个非匹配点的路径  ，使得匹配边和非匹配边在 上交替出现，那么称  是匹配 S 的增广路，也称交错路。

增广路显然具有以下性质：

1. 长度  是奇数
2. 路径上第  条边是非匹配边，第  条边是匹配边

正因为以上性质，我们把路径上所有边的状态取反，原来的匹配边变成非匹配边，原来的非匹配边变成匹配边，那么得到的新的边集  仍然是一组匹配，且匹配的边数增加了 1。进一步得到推论：

二分图的一组匹配 S 是最大匹配，当前结点图中不存在 S 的增广路。

---

匈牙利算法（增广路算法）

 匈牙利算法，又称增广路算法，用于计算二分图最大匹配。它的主要过程为：

1. 设 ，即所有的边都是非匹配边
2. 寻找增广路  ，把路径上的所有边的匹配状态取反，得到一个更大的匹配  
3. 重复第二步，直到图中不存在增广路

匈牙利算法的正确性基于贪心策略，它的一个重要特点是：当一个节点成为匹配点后，至多因为找到增广路二更换匹配对象，但是绝不会再变回非匹配点。

对于每个左部节点，寻找增广路至多遍历整个二分图一次。因此，该算法的时间复杂度是 

算法过程如下图演示：

最初的连接方式

第一次成功匹配

第二次成功匹配

 

第三次“调整”匹配

 

最后一次匹配

---

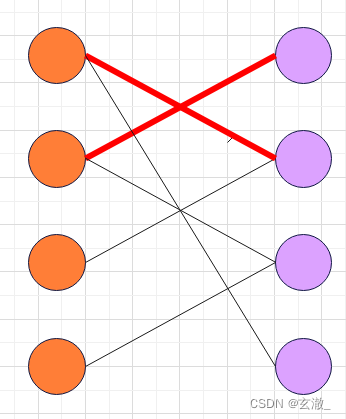
匈牙利代码实现 

 

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 510, M = 100010;

int n1, n2, m;
int h[N], ne[M], e[M], idx;
int match[N];  // 右部的点所对应的匹配
bool st[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

bool find(int x)
{
    for(int i = h[x]; ~i; i = ne[i])
    {
        int j = e[i];
        if(!st[j])
        {
            st[j] = true;
            if(match[j] == 0 || find(match[j]))
            {
                match[j] = x;
                return true;
            }
        }
    }
    return false;
}

int main()
{
    cin >> n1 >> n2 >> m;
    memset(h, -1, sizeof h);
    
    while(m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
    }
    
    int res = 0;
    for(int i = 1; i <= n1; i ++ )
    {
        memset(st, false, sizeof st);
        if(find(i)) res ++ ;
    }
    
    cout << res << endl;
    
    return 0;
}