当前位置:网站首页>Generate post order traversal according to pre order traversal and mid order traversal
Generate post order traversal according to pre order traversal and mid order traversal
2022-06-25 16:31:00 【GreyZeng】
author :Grey
Original address : Generate post order traversal according to pre order traversal and mid order traversal
Problem description
Cattle guest : Generate a postorder array through a preorder array and a meso array
Ideas
Suppose there is a binary tree

The result of preorder traversal is

The result of middle order traversal is

Because the scheduling logic of preorder traversal is , First , To the left , To the right
The scheduling logic of post order traversal is : First left , To the right , Re head .
therefore : The last node of post order traversal , It must be the head node of the preorder traversal .
Define recursive functions
// Traverse the array first pre Of [l1...r1] Section
// Middle order traversal array in Of [l2...r2] Section
// Generate post order traversal array pos Of [l3...r3] Section
void func(int[] pre, int l1, int r1, int[] in, int l2, int r2, int[] pos, int l3, r3)
According to the above inference , It can be concluded as follows
// The last node of post order traversal , It must be the head node of the preorder traversal
pos[r3] = pre[l1];
then , In an ordered array , We can locate the position of this header node , That is, the position marked with yellow in the figure below , Suppose this position is index,

This index The middle order array is divided into two parts , Because the scheduling process of middle order traversal is : First left , Re head , To the right , So in the middle order traversal [l2......index] Within the interval , In order to index The traversal result of the left tree with the position as the head ,[l2......index] The number of elements in the interval is assumed to be b, So in the preorder traversal , Count from top to bottom b Elements , namely :[l1......l1+b] It's made up of index The preorder traversal result of the left tree with the position as the head .
public static void func(int[] pre, int l1, int r1, int[] in, int l2, int r2, int[] pos, int l3, int r3) {
if (l1 > r1) {
// Avoidance of invalidity
return;
}
if (l1 == r1) {
// When there is only one number
pos[l3] = pre[l1];
} else {
// When there is more than one number
pos[r3] = pre[l1];
// index Indicates the position of a header in the ordered array
int index;
// Can be optimized
for (index = l2; index <= r2; index++) {
if (in[index] == pre[l1]) {
break;
}
}
int b = index - l2;
func(pre, l1 + 1, l1 + b, in, l2, index - 1, pos, l3, l3 + b - 1);
func(pre, l1 + b + 1, r1, in, index + 1, r2, pos, l3 + b, r3 - 1);
}
}
Optimize
In recursive functions func in , There is a traversal behavior ,
for (index = l2; index <= r2; index++) {
if (in[index] == pre[l1]) {
break;
}
}
If every recursion has to be traversed , Then the efficiency will be reduced , So you can set one at the beginning map, Save the location information of each value in the middle order traversal , This eliminates the need to traverse to find the location , The method is as follows :
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < n; i++) {
inOrder[i] = in.nextInt();
map.put(inOrder[i], i);
}
After this pretreatment , Every time index You don't need to traverse to get , It only needs
int index = map.get(pre[l1]);
that will do , For the full code, see
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] preOrder = new int[n];
int[] inOrder = new int[n];
for (int i = 0; i < n; i++) {
preOrder[i] = in.nextInt();
}
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < n; i++) {
inOrder[i] = in.nextInt();
map.put(inOrder[i], i);
}
int[] posOrder = new int[n];
func(preOrder, 0, n - 1, inOrder, 0, n - 1, posOrder, 0, n - 1, map);
for (int i = 0; i < n; i++) {
System.out.print(posOrder[i] + " ");
}
in.close();
}
public static void func(int[] pre, int l1, int r1, int[] in, int l2, int r2, int[] pos, int l3, int r3, Map<Integer, Integer> map) {
if (l1 > r1) {
// Avoidance of invalidity
return;
}
if (l1 == r1) {
// When there is only one number
pos[l3] = pre[l1];
} else {
// When there is more than one number
pos[r3] = pre[l1];
// index Indicates the position of a header in the ordered array
int index = map.get(pre[l1]);
int b = index - l2;
func(pre, l1 + 1, l1 + b, in, l2, index - 1, pos, l3, l3 + b - 1, map);
func(pre, l1 + b + 1, r1, in, index + 1, r2, pos, l3 + b, r3 - 1, map);
}
}
}
more
边栏推荐
- This article will help you understand the common concepts, advantages and disadvantages of JWT
- Day_ eleven
- When inputting text in the shutter textfield, if the page is refreshed, the cursor position will change.
- Day_ 16 set
- Xinlou: un voyage de sept ans de Huawei Sports Health
- [problem solving] dialogfragment can not be attached to a container view
- Uniapp converts graphic verification codes in the form of file streams into images
- The first day of reading mysql45
- Principle analysis of ThreadLocal source code
- error Parsing error: Unexpected reserved word ‘await‘.
猜你喜欢

Xinlou: Huawei's seven-year building journey of sports health

Android修行手册之Kotlin - 自定义View的几种写法

What exactly is a handler

error Parsing error: Unexpected reserved word ‘await‘.

心樓:華為運動健康的七年築造之旅

Sleep formula: how to cure bad sleep?

Day_ thirteen

What can one line of code do?
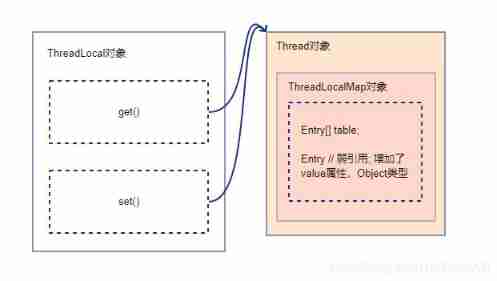
Principle analysis of ThreadLocal source code

Day_ 18 hash table, generic
随机推荐
Webgl and webgpu comparison [4] - uniform
DOM event flow, event delegate
Day_ 04
DINO: DETR with Improved DeNoising Anchor Boxes for End-to-End Object Detection翻译
Multiple decorators decorate a function
Vscode有什么好用的插件?
About the use of Aidl, complex data transmission
解析数仓lazyagg查询重写优化
Learning notes of rxjs takeuntil operator
ncnn源码学习全集
Overall MySQL architecture and statement execution process
数据存储和传输文件之XML使用和解析详解
DDD概念复杂难懂,实际落地如何设计代码实现模型?
Day_ 18 hash table, generic
Alvaria announces Jeff cotten, a veteran of the customer experience industry, as its new CEO
uniapp实现图片(单张/多张)预览
User login 2
Common APIs and exception mechanisms
Data type variable operator
Kettle表输入组件精度丢失的问题