当前位置:网站首页>《canvas》之第3章 曲线图形
《canvas》之第3章 曲线图形
2022-06-24 06:44:00 【yxqq378287007】
《canvas》之第3章 曲线图形
第3章 曲线图形
3.1 曲线图形简介
弧线是圆的一部分,弧线上的每个点都具有相同的曲率,曲线包含弧线。
3.2 圆形
3.2.1 圆形简介
cxt.beginPath();
cxt.arc(x, y, 半径, 开始角度, 结束角度, anticlockwise);
cxt.closePath();
开始角度和结束角度使用弧度,比如360*Math.PI/180。
anticlockwise默认false,顺时针方向。
3.2.2 描边圆
cxt.beginPath();
cxt.arc(x, y, 半径, 开始角度, 结束角度, anticlockwise);
cxt.closePath();
cxt.strokeStyle = "颜色值";
cxt.stroke();
- 圆
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title></title>
<meta charset="utf-8" />
<script type="text/javascript"> function $$(id) {
return document.getElementById(id); } window.onload = function () {
var cnv = $$("canvas"); var cxt = cnv.getContext("2d"); //整圆 cxt.beginPath(); cxt.arc(120, 80, 50, 0, 360 * Math.PI / 180); //cxt.closePath(); //描边 cxt.strokeStyle = "HotPink"; cxt.stroke(); //半圆 cxt.beginPath(); cxt.arc(80, 80, 50, 0, 180 * Math.PI / 180, true); cxt.closePath(); //描边 cxt.strokeStyle = "HotPink"; cxt.stroke(); } </script>
</head>
<body>
<canvas id="canvas" width="200" height="150" style="border:1px dashed gray;"></canvas>
</body>
</html>
- 弧形
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title></title>
<meta charset="utf-8" />
<script type="text/javascript"> function $$(id) {
return document.getElementById(id); } window.onload = function () {
var cnv = $$("canvas"); var cxt = cnv.getContext("2d"); cxt.beginPath(); cxt.arc(70, 70, 50, 0, -90 * Math.PI / 180, true); cxt.closePath(); cxt.strokeStyle = "HotPink"; cxt.stroke(); } </script>
</head>
<body>
<canvas id="canvas" width="200" height="150" style="border:1px dashed gray;"></canvas>
</body>
</html>
3.2.3 填充圆
cxt.beginPath();
cxt.arc(x, y, 半径, 开始角度, 结束角度, anticlockwise);
cxt.closePath();
cxt.fillStyle = "颜色值";
cxt.fill();
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title></title>
<meta charset="utf-8" />
<script type="text/javascript"> function $$(id) {
return document.getElementById(id); } window.onload = function () {
var cnv = $$("canvas"); var cxt = cnv.getContext("2d"); //整圆 cxt.beginPath(); cxt.arc(120, 80, 50, 0, 360 * Math.PI / 180); //cxt.closePath(); //描边 cxt.fillStyle = "#9966FF"; cxt.fill(); //半圆 cxt.beginPath(); cxt.arc(80, 80, 50, 0, 180 * Math.PI / 180, true); cxt.closePath(); //描边 cxt.fillStyle = "HotPink"; cxt.fill(); } </script>
</head>
<body>
<canvas id="canvas" width="200" height="150" style="border:1px dashed gray;"></canvas>
</body>
</html>
3.3 弧线
arc()和arcTo()。
3.3.1 arc()方法画弧线
cxt.beginPath();
cxt.arc(x, y, 半径, 开始角度, 结束角度, anticlockwise);
cxt.strokeStyle = "颜色值";
cxt.stroke();
anticlockwise默认false,顺时针方向。
- 弧线
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title></title>
<meta charset="utf-8" />
<script type="text/javascript"> function $$(id) {
return document.getElementById(id); } window.onload = function () {
var cnv = $$("canvas"); var cxt = cnv.getContext("2d"); cxt.beginPath(); cxt.arc(70, 70, 50, 0, -90 * Math.PI / 180, true); //cxt.closePath(); //闭合 cxt.stroke(); } </script>
</head>
<body>
<canvas id="canvas" width="200" height="150" style="border:1px dashed gray;"></canvas>
</body>
</html>
- 弧线+直线
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title></title>
<meta charset="utf-8" />
<script type="text/javascript"> function $$(id) {
return document.getElementById(id); } window.onload = function () {
var cnv = $$("canvas"); var cxt = cnv.getContext("2d"); //绘制一条直线 //cxt.beginPath(); cxt.moveTo(20, 20); cxt.lineTo(70, 20); cxt.stroke(); //绘制圆弧+直线 cxt.beginPath(); cxt.arc(70, 70, 50, 0, -90 * Math.PI / 180, true); cxt.moveTo(120, 70); cxt.lineTo(120, 120); cxt.stroke(); /* //绘制一条直线 cxt.beginPath(); cxt.moveTo(20, 20); cxt.lineTo(70, 20); cxt.stroke(); //绘制圆弧 cxt.beginPath(); cxt.arc(70, 70, 50, 0, -90 * Math.PI / 180, true); cxt.stroke(); //绘制一条直线 cxt.beginPath(); cxt.moveTo(120, 70); cxt.lineTo(120, 120); cxt.stroke(); */ } </script>
</head>
<body>
<canvas id="canvas" width="200" height="150" style="border:1px dashed gray;"></canvas>
</body>
</html>
3.3.2 arcTo()方法画弧线
cxt.arcTo(cx, cy, x2, y2, radius)
cx, cy控制点坐标
x2,y2结束点坐标
x1,y1开始点坐标,moveTo()或lineTo()提供。
arcTo()利用开始点、控制点、结束点形成的夹角,绘制与一段与夹角两边相切且半径为radius的短的圆弧。当开始点不是圆弧起点时,会绘制开始点到圆弧起点的直线。弧线
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title></title>
<meta charset="utf-8" />
<script type="text/javascript"> function $$(id) {
return document.getElementById(id); } window.onload = function () {
var cnv = $$("canvas"); var cxt = cnv.getContext("2d"); cxt.moveTo(20, 20); //cxt.lineTo(70, 20); cxt.arcTo(120, 20, 120, 70, 50); cxt.lineTo(120, 120); cxt.stroke(); } </script>
</head>
<body>
<canvas id="canvas" width="200" height="150" style="border:1px dashed gray;"></canvas>
</body>
</html>
- 圆角矩形
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title></title>
<meta charset="utf-8" />
<script type="text/javascript"> function $$(id) {
return document.getElementById(id); } window.onload = function () {
var cnv = $$("canvas"); var cxt = cnv.getContext("2d"); cxt.moveTo(40, 20); cxt.lineTo(160, 20); cxt.arcTo(180, 20, 180, 40, 20); cxt.moveTo(180, 40); cxt.lineTo(180, 110); cxt.arcTo(180, 130, 160, 130, 20); cxt.moveTo(160, 130); cxt.lineTo(40, 130); cxt.arcTo(20, 130, 20, 110, 20); cxt.moveTo(20, 110); cxt.lineTo(20, 40); cxt.arcTo(20, 20, 40, 20, 20); cxt.stroke(); } </script>
</head>
<body>
<canvas id="canvas" width="200" height="150" style="border:1px dashed gray;"></canvas>
</body>
</html>
- 圆角矩形函数封装
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title></title>
<meta charset="utf-8" />
<script type="text/javascript"> function $$(id) {
return document.getElementById(id); } window.onload = function () {
var cnv = $$("canvas"); var cxt = cnv.getContext("2d"); createRoundedRect(cxt, 100, 100, 20, 20, 20); cxt.fillStyle = "HotPink"; cxt.fill(); } /* * createRoundedRect()用于绘制圆角矩形 * width、height:分别表示长和宽 * r:表示圆角半径 * offsetX、offsetY:分别表示左上角顶点坐标 */ function createRoundedRect(cxt, width, height, r, offsetX, offsetY) {
cxt.beginPath(); cxt.moveTo(offsetX + r, offsetY); //cxt.lineTo(offsetX + width - r, offsetY); cxt.arcTo(offsetX + width, offsetY, offsetY + width, offsetY + r, r); //cxt.lineTo(offsetX + width, offsetY + height - r); cxt.arcTo(offsetX + width, offsetY + height, offsetX + width - r, offsetY + height, r); //cxt.lineTo(offsetX + r, offsetY + height); cxt.arcTo(offsetX, offsetY + height, offsetX, offsetY + height - r, r); //cxt.lineTo(offsetX, offsetY + r); cxt.arcTo(offsetX, offsetY, offsetX + r, offsetY, r); //cxt.closePath(); } </script>
</head>
<body>
<canvas id="canvas" width="200" height="150" style="border:1px dashed gray;"></canvas>
</body>
</html>
3.4 二次贝塞尔曲线
cxt.quadraticCurveTo(cx, cy, x2, y2);
cx,cy控制点坐标,x2,y2结束点坐标。
moveTo()或lineTo()提供开始点。
- 二次贝塞尔曲线
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title></title>
<meta charset="utf-8" />
<script type="text/javascript"> function $$(id) {
return document.getElementById(id); } window.onload = function () {
var cnv = $$("canvas"); var cxt = cnv.getContext("2d"); cxt.moveTo(30, 120); cxt.quadraticCurveTo(100, 20, 160, 120); cxt.stroke(); } </script>
</head>
<body>
<canvas id="canvas" width="200" height="150" style="border:1px dashed gray;"></canvas>
</body>
</html>
- 二次贝塞尔曲线画气泡
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title></title>
<meta charset="utf-8" />
<script type="text/javascript"> function $$(id) {
return document.getElementById(id); } window.onload = function () {
var cnv = $$("canvas"); var cxt = cnv.getContext("2d"); cxt.moveTo(75, 25); cxt.quadraticCurveTo(25, 25, 25, 62); cxt.quadraticCurveTo(25, 100, 50, 100); cxt.quadraticCurveTo(50, 120, 30, 125); cxt.quadraticCurveTo(60, 120, 65, 100); cxt.quadraticCurveTo(125, 100, 125, 62); cxt.quadraticCurveTo(125, 25, 75, 25); cxt.stroke(); } </script>
</head>
<body>
<canvas id="canvas" width="200" height="150" style="border:1px dashed gray;"></canvas>
</body>
</html>
3.5 三次贝塞尔曲线
cxt.bezierCurveTo(cx1, cy1, cx2, cy2,x2, y2);
cx1,cy1控制点1坐标,cx2,cy2控制点2坐标,x2,y2结束点坐标。
moveTo()或lineTo()提供开始点。
- 三次贝塞尔曲线
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title></title>
<meta charset="utf-8" />
<script type="text/javascript"> function $$(id) {
return document.getElementById(id); } window.onload = function () {
var cnv = $$("canvas"); var cxt = cnv.getContext("2d"); //绘制三次贝塞尔曲线 var startX = 20; var startY = 80; var cx1 = 20; var cy1 = 20; var cx2 = 120; var cy2 = 120; var endX = 120; var endY = 60; cxt.moveTo(startX, startY); cxt.bezierCurveTo(cx1, cy1, cx2, cy2, endX, endY); cxt.stroke(); } </script>
</head>
<body>
<canvas id="canvas" width="200" height="150" style="border:1px dashed gray;"></canvas>
</body>
</html>
- 三次贝塞尔曲线画心形
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title></title>
<meta charset="utf-8" />
<script type="text/javascript"> function $$(id) {
return document.getElementById(id); } window.onload = function () {
var cnv = $$("canvas"); var cxt = cnv.getContext("2d"); cxt.moveTo(75, 40); cxt.bezierCurveTo(75, 37, 70, 25, 50, 25); cxt.bezierCurveTo(20, 25, 20, 62.5, 20, 62.5); cxt.bezierCurveTo(20, 80, 40, 102, 75, 120); cxt.bezierCurveTo(110, 102, 130, 80, 130, 62.5); cxt.bezierCurveTo(130, 62.5, 130, 25, 100, 25); cxt.bezierCurveTo(85, 25, 75, 37, 75, 40); cxt.stroke(); } </script>
</head>
<body>
<canvas id="canvas" width="200" height="150" style="border:1px dashed gray;"></canvas>
</body>
</html>
- 贝塞尔曲线画N叶草
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title></title>
<meta charset="utf-8" />
<script type="text/javascript"> function $$(id) {
return document.getElementById(id); } window.onload = function () {
var cnv = $$("canvas"); var cxt = cnv.getContext("2d"); var n = 5; var rMin = 20*0.4; var rMax = 80*1.5; createLeaf(cxt, n, cnv.width/2, cnv.height/2, rMin, rMax); cxt.fillStyle = "#00FF99";//浅绿色 cxt.fill(); } /* * createLeaf()用于绘制N叶草 * n:n片 * centerX、centerY:花朵中心位置的坐标 * rMin:控制花朵的大小 * rMax:控制花瓣长度 */ function createLeaf(cxt, n, centerX, centerY, rMin, rMax) {
cxt.beginPath(); cxt.moveTo(centerX, centerY + rMin); var degree = 2*Math.PI/n; for (var i = 1; i < n + 1; i++) {
//计算控制点坐标 var cx1 = centerX + rMax * Math.sin((i - 1) * degree); var cy1 = centerY + rMax * Math.cos((i - 1) * degree); var cx2 = centerX + rMax * Math.sin(i * degree); var cy2 = centerY + rMax * Math.cos(i * degree); //计算结束点的坐标 var x = centerX + rMin * Math.sin(i * degree); var y = centerY + rMin * Math.cos(i * degree); cxt.bezierCurveTo(cx1, cy1, cx2, cy2, x, y); } cxt.closePath(); } </script>
</head>
<body>
<canvas id="canvas" width="200" height="150" style="border:1px dashed gray;"></canvas>
</body>
</html>
<!-- 这里,我们在一条路径中连续定义首尾相连的多段贝塞尔曲线,其中每段三次贝塞尔曲线的起点和终点都落在圆心为(centerX, centerY)、半径为rMin的圆上,而每段圆弧的两个控制点落在圆心为(centerX, centerY)、半径为rMax的圆上,于是形成了N叶草的图形。其中,起点、终点和控制点坐标是使用正弦和余弦函数计算出来的。 总的来说,使用二次或三次贝塞尔曲线来绘制一个图形是相当有挑战的,因为这不像在矢量绘图软件Adobe Illustrator(简称AI)里那样有即时的视觉反馈(所见即所得)。所以用它来画复杂图形比较麻烦。但是从理论上来说,任何复杂的图形都可以用贝塞尔曲线绘制出来!这也是贝塞尔曲线强大之处。 -->
3.6 绘制扇形
- 扇形
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title></title>
<meta charset="utf-8" />
<script type="text/javascript"> function $$(id) {
return document.getElementById(id); } window.onload = function () {
var cnv = $$("canvas"); var cxt = cnv.getContext("2d"); cxt.beginPath(); cxt.moveTo(100, 75); cxt.arc(cnv.width/2, cnv.height/2, 50, 30*Math.PI/180, 120*Math.PI/180, false); cxt.closePath(); cxt.strokeStyle = "HotPink"; cxt.stroke(); } </script>
</head>
<body>
<canvas id="canvas" width="200" height="150" style="border:1px dashed gray;"></canvas>
</body>
</html>
- 扇形函数封装
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title></title>
<meta charset="utf-8" />
<script type="text/javascript"> function $$(id) {
return document.getElementById(id); } window.onload = function () {
var cnv = $$("canvas"); var cxt = cnv.getContext("2d"); createSector(cxt, cnv.width/2, cnv.height/2, 50, 30, 120); cxt.fillStyle = "HotPink"; cxt.fill(); } function createSector(cxt, x, y, r, angle1, angle2) {
cxt.beginPath(); cxt.moveTo(x, y); cxt.arc(x, y, r, angle1*Math.PI/180, angle2*Math.PI/180, false); cxt.closePath(); } </script>
</head>
<body>
<canvas id="canvas" width="200" height="150" style="border:1px dashed gray;"></canvas>
</body>
</html>
边栏推荐
- Combine with (& &) logic or (||), dynamic binding and ternary operation
- 什么是CC攻击?如何判断网站是否被CC攻击? CC攻击怎么防御?
- [WordPress website] 6 Article content copy prevention
- Cisco router configuration notes: static routing, rip, OSPF, principles combined with experiments, worth a visit!
- Alibaba cloud full link data governance
- Lend you a pair of insight, Frida native trace
- RDD basic knowledge points
- When MFC uses the console, the project path cannot have spaces or Chinese, otherwise an error will be reported. Lnk1342 fails to save the backup copy of the binary file to be edited, etc
- [signal recognition] signal modulation classification based on deep learning CNN with matlab code
- Pyhton crawls to Adu (Li Yifeng) Weibo comments
猜你喜欢

jarvisoj_ level2

bjdctf_ 2020_ babystack
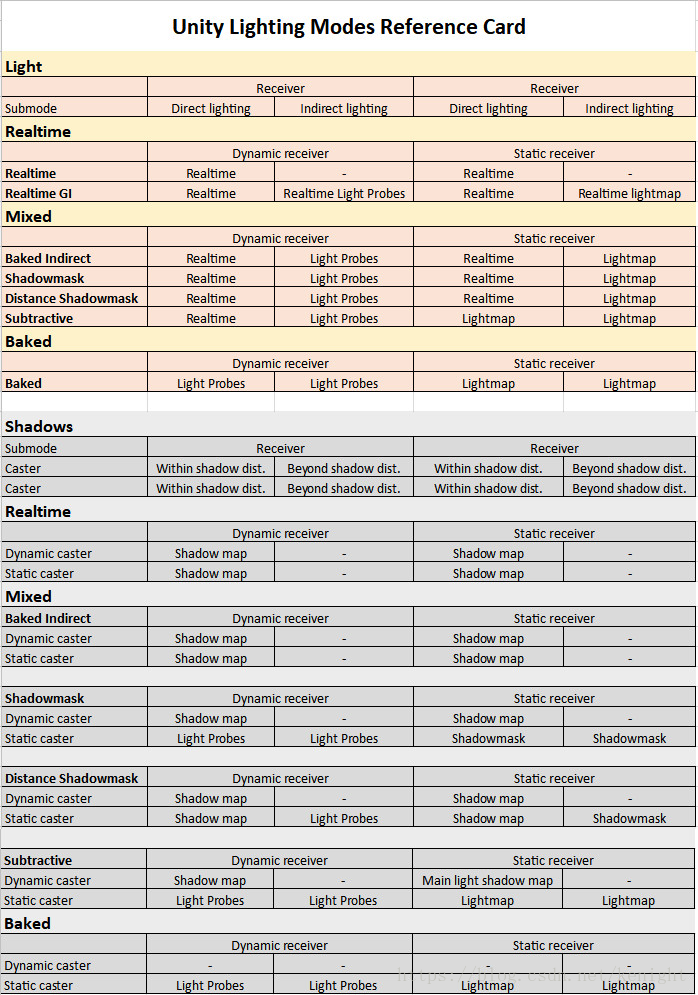
光照使用的简单总结
![[image segmentation] retinal vessel segmentation based on morphology with matlab code](/img/e3/0805df81a597346ea7c2d2da20ac96.png)
[image segmentation] retinal vessel segmentation based on morphology with matlab code
![[image fusion] image fusion based on pseudo Wigner distribution (PWD) with matlab code](/img/e0/14cd7982fb3059fed235470d91126e.png)
[image fusion] image fusion based on pseudo Wigner distribution (PWD) with matlab code
![[image fusion] multi focus and multi spectral image fusion based on pixel saliency and wavelet transform with matlab code](/img/78/5d8ad56d4ff1451590cc8676893f05.png)
[image fusion] multi focus and multi spectral image fusion based on pixel saliency and wavelet transform with matlab code
![[GUET-CTF2019]zips](/img/79/22ff5d4a3cdc3fa9e0957ccc9bad4b.png)
[GUET-CTF2019]zips

How to connect the Bluetooth headset to the computer and how to connect the win10 computer to the Bluetooth headset

Learning to use BACnet gateway of building control system is not so difficult
![[image fusion] image fusion based on NSST and PCNN with matlab code](/img/b4/61a5adde0d0bfc5a339ef8ab948d43.png)
[image fusion] image fusion based on NSST and PCNN with matlab code
随机推荐
2.1.1 QML grammar foundation I
C code writing specification
How to turn on win11 notebook power saving mode? How to open win11 computer power saving mode
[GUET-CTF2019]zips
Lend you a pair of insight, Frida native trace
[WordPress website] 5 Set code highlight
Hubei College Upgraded to undergraduate - Hushi family planning department
[DDCTF2018](╯°□°)╯︵ ┻━┻
[signal recognition] signal modulation classification based on deep learning CNN with matlab code
Global and Chinese markets for food puffers 2022-2028: Research Report on technology, participants, trends, market size and share
How to distinguish PAAS, IAAs and SaaS?
A summary of the posture of bouncing and forwarding around the firewall
Black box and white box models for interpretable AI
什么是CC攻击?如何判断网站是否被CC攻击? CC攻击怎么防御?
MaxCompute远程连接,上传、下载数据文件操作
Session & cookie details
Global and Chinese market of anion sanitary napkins 2022-2028: Research Report on technology, participants, trends, market size and share
What should I pay attention to after the live broadcast system source code is set up?
MSSQL high permission injection write horse to Chinese path
[Proteus] Arduino uno + ds1307+lcd1602 time display