当前位置:网站首页>2160. 拆分数位后四位数字的最小和
2160. 拆分数位后四位数字的最小和
2022-06-25 06:41:00 【AlbertOS】
引入
给你一个四位 正 整数 n u m num num 。请你使用 n u m num num 中的 数位 ,将 n u m num num 拆成两个新的整数 n e w 1 new1 new1 和 n e w 2 new2 new2 。
n e w 1 new1 new1 和 n e w 2 new2 new2 中可以有 前导 0 ,且 num 中 所有 数位都必须使用。
比方说,给你 num = 2932 ,你拥有的数位包括:两个 2 ,一个 9 和一个 3 。一些可能的 [new1, new2] 数对为 [22, 93],[23, 92],[223, 9] 和 [2, 329] 。
请你返回可以得到的 new1 和 new2 的 最小 和。
示例
输入:num = 2932
输出:52
解释:可行的 [new1, new2] 数对为 [29, 23] ,[223, 9] 等等。
最小和为数对 [29, 23] 的和:29 + 23 = 52 。
输入:num = 4009
输出:13
解释:可行的 [new1, new2] 数对为 [0, 49] ,[490, 0] 等等。
最小和为数对 [4, 9] 的和:4 + 9 = 13 。
题解
这个题目的意思看示例就明白一点了,是一个四位的正整数,就说明在这个整数中找到两个最小的当做第一和第二个数对的十位,剩下的就是两者的个位,这样就是最小和。
很明显的贪心法,我们将当前较小的数值放在较高位,用数组存储 n u m num num的每个的数值,然后升序排序,则最小和为 10 ∗ ( d i g [ 0 ] + d i g [ 1 ] ) + ( d i g [ 2 ] + d i g [ 3 ] ) 10 * (dig[0]+dig[1])+(dig[2]+dig[3]) 10∗(dig[0]+dig[1])+(dig[2]+dig[3])
class Solution {
public:
int minimumSum(int num) {
vector<int> digits;
//将每个数值位存入数组
while (num) {
digits.push_back(num % 10);
num /= 10;
}
//数组升序排序
sort(digits.begin(), digits.end());
return 10 * (digits[0] + digits[1]) + digits[2] + digits[3];
}
};
边栏推荐
- Misunderstanding of switching triode
- Research on 3D model retrieval method based on two channel attention residual network - Zhou Jie - paper notes
- 图扑软件数字孪生 3D 风电场,智慧风电之海上风电
- 國外LEAD域名郵箱獲取途徑
- [pytest] modify the logo and parameterization in the allure Report
- OAuth 2.0 one click login
- 搞清信息化是什么,让企业转型升级走上正确的道路
- STL教程4-输入输出流和对象序列化
- [batch dos-cmd command - summary and summary] - commands related to Internet access and network communication (Ping, Telnet, NSLOOKUP, ARP, tracert, ipconfig)
- Ns32f103c8t6 can perfectly replace stm32f103c8t6
猜你喜欢
![Different paths ii[dynamic planning improvement for DFS]](/img/bb/1e1cee22b9de954de242d299a1a0eb.png)
Different paths ii[dynamic planning improvement for DFS]

Three years of continuous decline in revenue, Tiandi No. 1 is trapped in vinegar drinks

数据可视化没有重点怎么办?
![[batch dos-cmd command - summary and summary] - commands related to Internet access and network communication (Ping, Telnet, NSLOOKUP, ARP, tracert, ipconfig)](/img/9b/283d99adf10262c356d1a87ce01bc0.png)
[batch dos-cmd command - summary and summary] - commands related to Internet access and network communication (Ping, Telnet, NSLOOKUP, ARP, tracert, ipconfig)

Chuantu microelectronics ca-if1051 can-fd transceiver

Summary of small problems in smartbugs installation
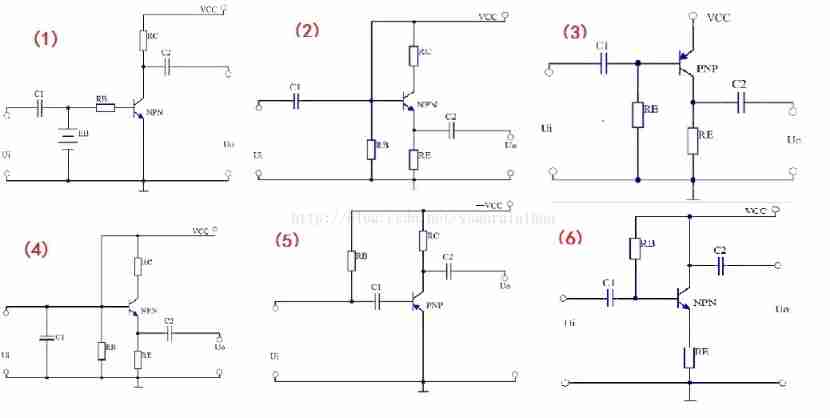
The method of judging whether triode can amplify AC signal

Terms and concepts related to authority and authentication system
![[batch dos-cmd command - summary and summary] - CMD window setting and operation commands (CD, title, mode, color, pause, CHCP, exit)](/img/8c/7345b4e8a55dcf11d18ac113df4fc2.png)
[batch dos-cmd command - summary and summary] - CMD window setting and operation commands (CD, title, mode, color, pause, CHCP, exit)
Debian introduction
随机推荐
STL tutorial 4- input / output stream and object serialization
权限、认证系统相关名词概念
Five causes of PCB board deformation and six solutions 2021-10-08
NPM install reports an error: gyp err! configure error
Cglib dynamic proxy
C#入门教程
Lebel only wants an asterisk in front of it, but doesn't want to verify it
CGLIB动态代理
How to use printf of 51 single chip microcomputer
GUI pull-down menu of unity3d evil door implementation dropdown design has no duplicate items
What is the difference between norflash and nandflash
C get the version number of exe - file version and assembly version
Function template_ Class template
微信小程序开通客服消息功能开发
VectorDraw Web Library 10.10
WinForm实现窗口始终在顶层
IAR compiler flashback
Distributed quorum NWR of the alchemy furnace of the Supreme Master
[Batch dos - cmd Command - Summary and Summary] - cmd extension Command, extension Function (CMD / E: on, CMD / E: off)
Evolution of Alibaba e-commerce architecture