Arbre binaire partie 1

Arbre binaire

Structure arborescente

L'arbre est une structure de données non linéaire,C'est fait parn（n>=0）Les noeuds finis forment un ensemble de relations hiérarchiques.On l'appelle un arbre parce qu'il ressemble à un arbre à l'envers,C'est - à - dire qu'il est orienté vers le Haut,Et les feuilles vers le bas.

Il présente les caractéristiques suivantes:：Il y a un noeud spécial,Appelé noeud racine,

Le noeud racine n'a pas de noeud avantÀ l'exception du noeud racine,

Les autres noeuds sont divisés enM(M > 0)Ensembles disjointsT1、T2、…、Tm,Chacune de ces collections Ti (1 <= i<= m) Un autre sous - arbre semblable à un arbre.

Le noeud racine de chaque sous - arbre a et n'a qu'un seul précurseur,Oui.0Un ou plusieurs successeurs
L'arbre est défini Récursivement.

Concept（Important）

J'ai compris. Concept Alors Comment? Représentation Où sont les arbres? ？？？

Représentation de l'arbre

La structure de l'arbre est relativement compliquée par rapport aux tableaux linéaires,Il est difficile de stocker la représentation,En fait, il y a beaucoup de façons dont les arbres sont représentés,Par exemple:：Représentation parentale,
Représentation des enfants、La représentation des enfants, des frères, etc..Voici un aperçu de ce qui est le plus commun** Le frère de l'enfant a dit

2、Arbre binaire

Un arbre binaire est un ensemble fini de noeuds,La collection est soit vide,Ou par un noeud racine plus deux binaires appelés sous - arbres de gauche et de droite
Composition des arbres.
Les caractéristiques des arbres binaires：

1. Jusqu'à deux sous - arbres par noeud,C'est - à - dire que l'absence d'arbre binaire est supérieure à 2 Node of.

2. Les sous - arbres de l'arbre binaire sont divisés à gauche et à droite,L'ordre de ses sous - arbres ne peut être inversé,Donc l'arbre binaire est un arbre ordonné.

   （Ordre. Non, pas du tout. Ordre de taille Mais... Ordre）
   

Deux arbres binaires spéciaux

Concept ：

1. Arbre binaire plein: Un arbre binaire,.Si le nombre maximum de noeuds est atteint pour chaque couche,Alors cet arbre binaire est plein d'arbres binaires.C'est - à - dire,Si
   Le nombre de couches d'un arbre binaire estK,Et le nombre total de noeuds est ,C'est un arbre binaire.
2. Arbre binaire complet: L'arbre binaire complet est une structure de données très efficace,Un arbre binaire complet est tiré d'un arbre binaire complet.Pour une profondeur deKDe,Oui.n
   Arbre binaire à noeuds,Si et seulement si chacun de ses noeuds a une profondeur deKNombre dans l'arbre binaire complet de1ànLorsque les noeuds correspondent un par un, ils sont appelés complets.
   Arbre binaire. Notez que l'arbre binaire complet est un arbre binaire complet spécial.
   
   

De l'arbre binaire Nature

Après avoir vu la nature de l'arbre binaire, regardons le stockage de l'arbre binaire.

3、Stockage des arbres binaires

La structure de stockage de l'arbre binaire est divisée en：Stockage séquentiel et stockage en chaîne similaire à une liste liée

Ici, nous Compréhension principale Stockage en chaîne Et l'ordre Stockage Et Est couramment utilisé dans le tas

Le stockage en chaîne d'un arbre binaire est référencé par un noeud,Les représentations courantes sont binaires et tridimensionnelles,Les détails sont les suivants：

// Représentation des enfants
class Node {
    
int val; // Champ de données
Node left; // Citation de l'enfant de gauche,Un sous - arbre gauche entier qui représente souvent l'enfant gauche comme racine
Node right; // Citation de l'enfant de droite,Un sous - arbre droit entier qui représente souvent l'enfant droit comme racine
}


// Représentation parentale de l'enfant
class Node {
    
int val; // Champ de données
Node left; // Citation de l'enfant de gauche,Un sous - arbre gauche entier qui représente souvent l'enfant gauche comme racine
Node right; // Citation de l'enfant de droite,Un sous - arbre droit entier qui représente souvent l'enfant droit comme racine
Node parent; // Noeud racine du noeud courant
}

Création d'arbres binaires

Ici. Nous Créer un arbre binaire Sera utilisé Un très, très grincheux. Mode de création

Non, pas du tout. C'est vrai. Mode de création , On commence. Création Pour comprendre Un instant. Propriétés des arbres binaires


Joindre le Code

class BTNode {
    
    public char val;
    // Citation de l'enfant de gauche
    public BTNode left;
    // Enfant droit
    public BTNode right;
    public BTNode (char val) {
    
        this.val = val;
    }
}
public class BinaryTree {
    
    public BTNode root; // Noeud racine de l'arbre binaire

    public BTNode createTree() {
    
        BTNode A = new BTNode('A');
        BTNode B = new BTNode('B');
        BTNode C = new BTNode('C');
        BTNode D = new BTNode('D');
        BTNode E = new BTNode('E');
        BTNode F = new BTNode('F');
        BTNode G = new BTNode('G');
        BTNode H = new BTNode('H');
        A.left = B;
        A.right = C;
        B.left = D;
        B.right = E;
        C.left = F;
        C.right = G;
        E.right = H;
        return A;
    }
}

La traversée de l'arbre binaire（Points saillants）

3Une façon de traverser （ Le timing de l'accès à l'arbre binaire est différent ）

1.Traversée du préfixe（D'abord la racine traverse

2.Traversée de l'ordre moyen

3.Traversée ultérieure

Résumé

Après l'étude Arbre binaire De Trois traversées Comment Découverte Elles - Oui. Le long d'une route De,Je l'imprime. De Timing C'est différent.

Exercice

1.Mise en œuvre du Code

1.Traversée du préfixe Racine --》 Sous - arbre gauche --》 Sous - arbre droit

 // Adoption Récursion  Mise en œuvre de la traversée préformée 
    void preOrder(BTNode root) {
    
        if(root == null) {
    
            return;
        }
        System.out.print(root.val + " ");
        preOrder(root.left);
        preOrder(root.right);
    }

J'ai compris. Préface Traversée Alors Nous sommes directement Fais - le. Traversée du préfixe De oj Questions

Traversée pré - ordonnée de l'arbre binaire

Méthode 1 ：Traversée Idées

class Solution {
    
    //Ici. Garantie C'est list Tous Seulement Un exemplaire. 
    List<Integer> list = new ArrayList<>();
    public List<Integer> preorderTraversal(TreeNode root) {
    
        
        if(root == null) {
    
            return list;
        }
        list.add(root.val);
        preorderTraversal(root.left);
        preorderTraversal(root.right);  
        return list;
    }
}

Méthode 2 ： Idées sur les sous - Questions

class Solution {
    
    public List<Integer> preorderTraversal(TreeNode root) {
    
         List<Integer> list = new ArrayList<>();
        if(root == null) {
    
            return list;
        }
        list.add(root.val);
        List<Integer> leftTree = preorderTraversal(root.left);
        list.addAll(leftTree);
        List<Integer> rightTree = preorderTraversal(root.right);  
        list.addAll(rightTree);

        return list;
    }
}

· Je connais la préface. Traversée Alors Traversée de l'ordre moyen Et Traversée ultérieure Alors Non, c'est vrai. Ajuster Récursion L'ordre?

2.Traversée de l'ordre moyen Sous - arbre gauche --》 Racine --》 Sous - arbre droit

   // Traversée de l'ordre moyen
    // Sous - arbre gauche --》 Racine --》 Sous - arbre droit
    void inOrderTraversal(BTNode root) {
    
        if(root == null) {
    
            return;
        }
        inOrderTraversal(root.left);
        System.out.print(root.val+" ");
        inOrderTraversal(root.right);
    }

Traversée du milieu de l'arbre binaire

Méthode 1 ： Pensée ergodique

class Solution {
    
    List<Integer> list  = new ArrayList<>();
    public List<Integer> inorderTraversal(TreeNode root) {
    
        if(root == null) {
    
            return list;
        }
        inorderTraversal(root.left);
        list.add(root.val);
        inorderTraversal(root.right);
        return list;
    }
}

Méthode 2 ： Idées sur les sous - Questions

class Solution {
    
    public List<Integer> inorderTraversal(TreeNode root) {
    
        List<Integer> list = new ArrayList<>();
        if(root == null) {
    
            return list;
        }
        List<Integer> leftTree = inorderTraversal(root.left);
        list.addAll(leftTree);

        list.add(root.val);

        List<Integer> rightTree = inorderTraversal(root.right);
        list.addAll(rightTree);
        return list;
    }
}

3.Traversée postérieure Sous - arbre gauche --》Sous - arbre droit --》 Racine

    // Traversée postérieure
    // Sous - arbre droit --》 Sous - arbre gauche --》 Racine
    void postOrderTraversal(BTNode root) {
    
        if(root == null) {
    
            return;
        }
        inOrderTraversal(root.left);
        inOrderTraversal(root.right);
        System.out.print(root.val+" ");
    }

Traversée post - ordre de l'arbre binaire

Méthode 1 ： Pensée ergodique

class Solution {
    
    List<Integer> list = new ArrayList<>();
    public List<Integer> postorderTraversal(TreeNode root) {
    
        if(root == null) {
    
            return list;
        }
        postorderTraversal(root.left);
        postorderTraversal(root.right);
        list.add(root.val);
        return list;
    }
}

Méthode 2 ： Idées sur les sous - Questions

class Solution {
    
    public List<Integer> postorderTraversal(TreeNode root) {
    
        List<Integer> list = new ArrayList();

        if(root == null) {
    
            return list;
        }
        List<Integer> leftTree = postorderTraversal(root.left);
        list.addAll(leftTree);
        List<Integer> rightTree = postorderTraversal(root.right);
        list.addAll(rightTree);

        list.add(root.val);
        return list;
    }
}

Viens ici. Un idea Raccourcis clavier Changement global Variable name shift Plus f6

Traversée du programme

Que le nombre de couches où se trouve le noeud racine de l'arbre binaire est1,La traversée des séquences commence à partir du noeud racine de l'arbre binaire où,Accédez d'abord au noeud racine de l'arbre au premier niveau,Et de
Accès de gauche à droite 2Noeud sur la couche,Puis il y a les noeuds du troisième étage,Et ainsi de suite.,De haut en bas,Le processus d'accès aux noeuds de l'arbre couche par couche de gauche à droite est
Traversée séquentielle.

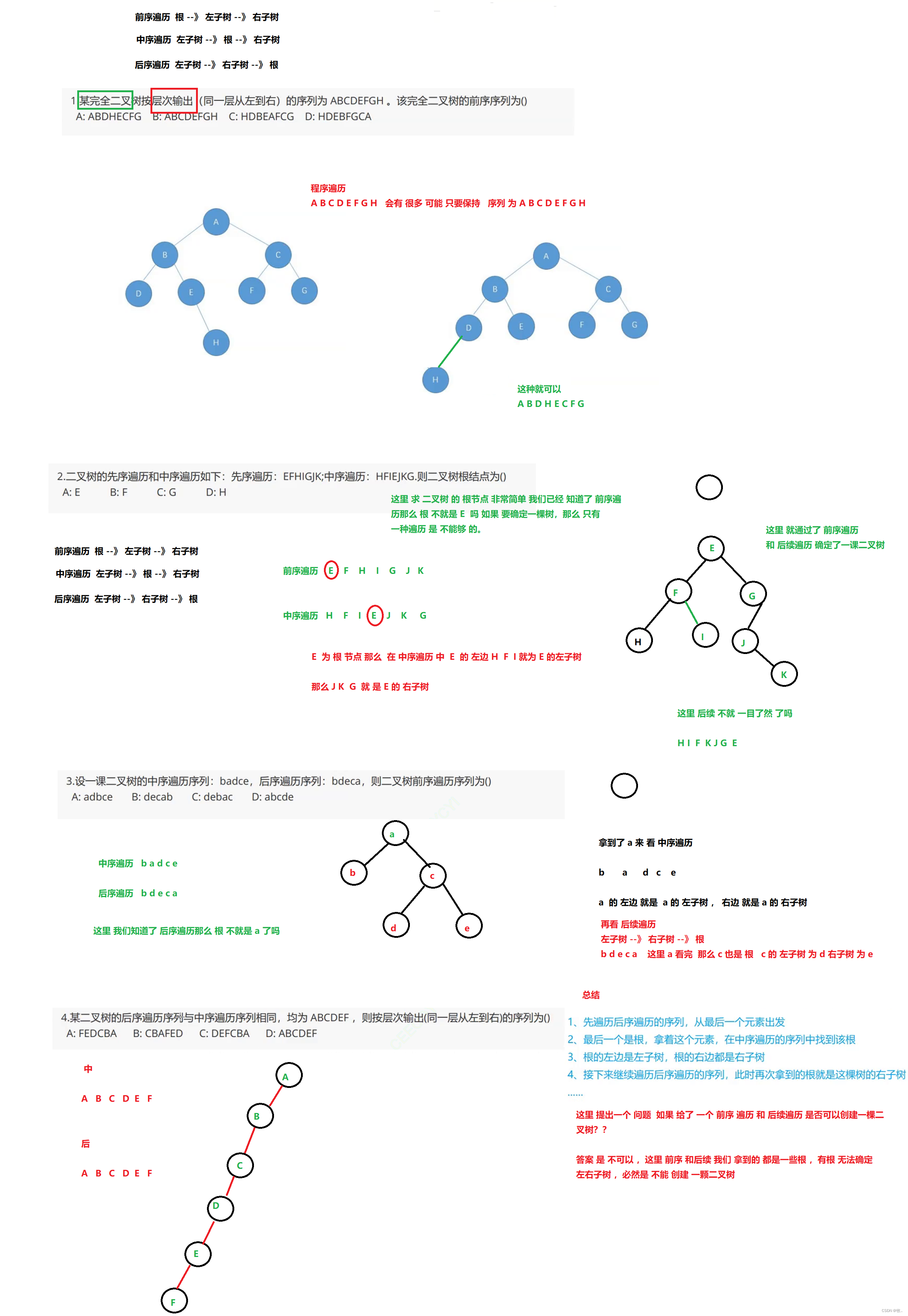
Enfin. 4Questions générales Fin Partie I Arbre binaire