当前位置:网站首页>[code Capriccio - dynamic planning] t583. Deleting two strings
[code Capriccio - dynamic planning] t583. Deleting two strings
2022-06-26 17:18:00 【Not blogging】
T583、 Deletion of two strings
Give two words word1 and word2 , Return makes word1 and word2 The same minimum number of steps required .
Every step You can delete a character from any string
Solution to the problem :
step1、dp[i][j] Express word1[0:i-1] and word2[0:j-1] To achieve equality , The minimum number of times an element needs to be deleted .
step2、 The recursive formula
When word1.charAt(i-1) == word2.charAt(j-1) When , be dp[i][j] = dp[i-1][j-1]
https://www.programmercarl.com/0583.%E4%B8%A4%E4%B8%AA%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E5%88%A0%E9%99%A4%E6%93%8D%E4%BD%9C.html
The second case is more complicated , When I write, I only consider dp[i][j-1]+1 This situation , It is equivalent to deleting only word2, So finally submit 159/1396
public int minDistance(String word1, String word2) {
int n = word1.length();
int m = word2.length();
// How to delete this logic
// Last question dp[i][j] Express word1[:i-1]
// word2[:j-1] The minimum number of steps
int[][] dp = new int[n+1][m+1];
for(int j = 0; j <= m; j++){
dp[0][j] = j;
}
for(int i = 0; i <= n; i++){
dp[i][0] = i;
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
if(word1.charAt(i-1) == word2.charAt(j-1)){
dp[i][j] = dp[i-1][j-1];
}else{
dp[i][j] = Math.min(dp[i-1][j-1]+2, Math.min(dp[i][j-1] + 1, dp[i-1][j]+1));
}
}
}
return dp[n][m];
}
边栏推荐
- Leetcode daily [2022 - 02 - 16]
- Community ownership of NFT trading market is unstoppable
- Leetcode 1170. Frequency of occurrence of the minimum letter of the comparison string (yes, solved)
- 【代码随想录-动态规划】T583、两个字符串的删除操作
- Teach you to learn dapr - 1 The era of net developers
- 【万字总结】以终为始,详细分析高考志愿该怎么填
- LeetCode——226. 翻转二叉树(BFS)
- COMP5216 Mobile Computing Assignment 1 - Extending ToDoList app
- 有依赖的背包问题
- Teach you to learn dapr - 9 Observability
猜你喜欢

分布式架构概述

Vue--vuerouter cache routing component

直播预告|程序员进击,如何提升研发效能?6月21日晚视频号、B站同步直播,不见不散!
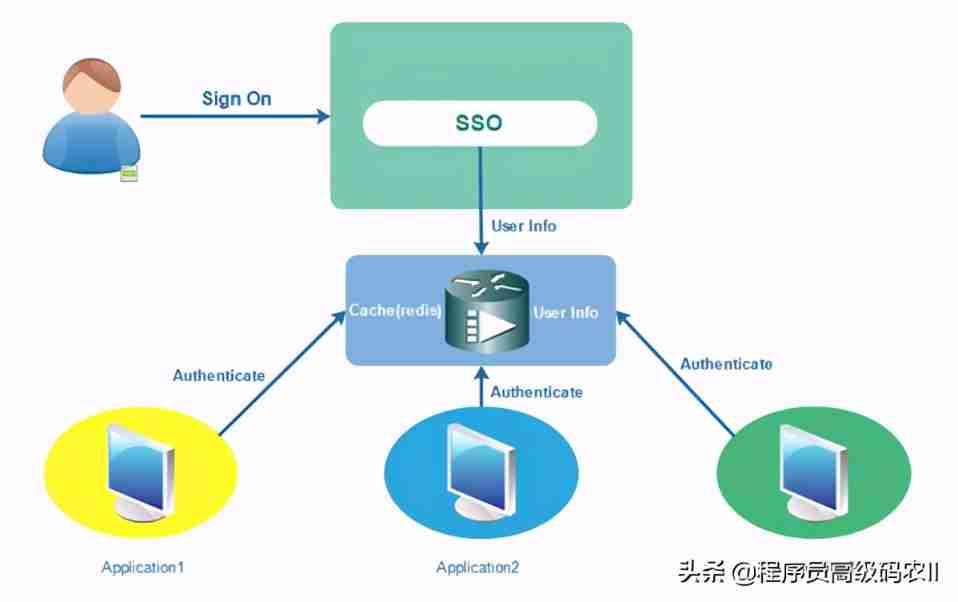
Microservice architecture practice: business management background and SSO design, SSO client design
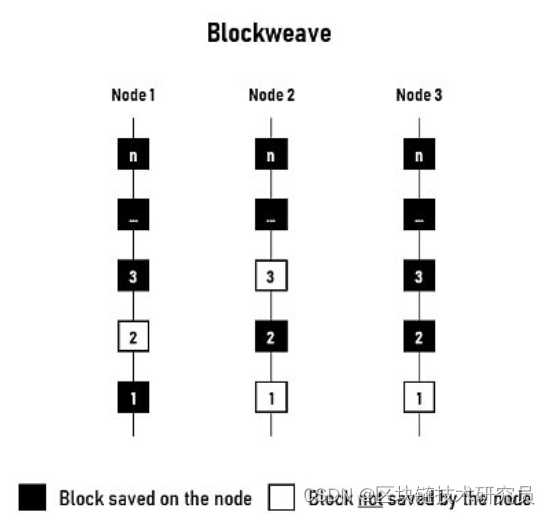
Web3 decentralized storage ecological landscape

Web3去中心化存储生态图景

Environment setup mongodb

【推荐系统学习】推荐系统的技术栈

Platform management background and merchant menu resource management: merchant registration management design

Leetcode 1170. Frequency of occurrence of the minimum letter of the comparison string (yes, solved)
随机推荐
Web3 decentralized storage ecological landscape
Here comes the hero League full skin Downloader
Microservice architecture practice: business management background and SSO design, SSO client design
Call the random function to generate 20 different integers and put them in the index group of institute a
Introduction to minimal API
Redis overview
Strength and appearance Coexist -- an exclusive interview with Liu Yu, a member of Apache pulsar PMC
合约量化系统开发方案详细,量化合约系统开发技术说明
Redis and database data consistency
Calculate a=1, a2=1/1=a1
Discover K8E: minimalist kubernetes distribution
20:第三章:开发通行证服务:3:在程序中,打通redis服务器;(仅仅是打通redis服务器,不涉及具体的业务开发)
halcon之区域:多种区域(Region)特征(5)
Synchronized description of concurrency
Uncover the secret of Agora lipsync Technology: driving portraits to simulate human speech through real-time voice
[ten thousand words summary] starting from the end, analyze in detail how to fill in the college entrance examination volunteers
Cloud native 02: Alibaba cloud cloud efficient flow pipeline
num[i]++
[qt learning notes]qt inter thread data communication and data sharing
Technical scheme design of chain game system development - NFT chain game system development process and source code