当前位置:网站首页>Research on stability of time-delay systems based on Lambert function
Research on stability of time-delay systems based on Lambert function
2022-07-24 15:23:00 【studyer_ domi】
1、 Content abstract
A little
426- Can communicate 、 consulting 、 Answering question
2、 Content description
With the development of network technology in today's world 、 The rapid development of communication technology and computer technology and their wide application in various fields . Especially in the research of power system , With the continuous development and innovation of Technology , Gradually applied to power production and power supply system , It provides a stable way of power transmission , Move towards intellectualization . These technologies also make the monitoring of power system 、 The analysis and control mode is towards wide area 、 Networking and intelligence , There is an important characteristic in the power system, that is, the time-delay characteristic , What we want to study is in the power system Lambert Stability of time-delay systems under function . For now , When domestic and foreign scholars analyze the power system , The influence of time-delay characteristics is ignored . But the composition of the power system is very complex 、 Gigantic , When high power needs long-distance transmission , The possibility and harm of power oscillation on the transmission line will become greater , It is difficult to ensure the stability of power system only by locally designed controller . And the power system is often a nonlinear 、 Time delay dynamical systems with randomness , The existence of time delay is the source of system instability , Even a small time delay will cause controller failure , Even cause catastrophic accidents , therefore , in many instances , The power system must be modeled as a time-delay system for research , Make good use of the stability of time-delay systems , The implementation of wide area optimal control from the perspective of the whole system can ensure the safe and stable operation of the system .
Time delay system is the inherent time delay of system components , Or the time delay system introduced for control purposes . Delay systems can be expressed by delay differential equations , It belongs to a class of universal differential equations , And a lot of research has been done in the past decades . From power and automation engineering to biology 、 chemical 、 Physical systems and ecology , Will quote time delay . Such a time delay can limit and reduce the achievable performance of the control system , It may even cause system instability . In various time-delay systems , The pure delay time of the object has great harm to the control performance of the control system , It not only reduces the stability of the system , The characteristics of the transition process deteriorate , And the longer the pure lag takes up the whole dynamic process , The more difficult it is to control , Therefore, the control problem of time-delay systems has become a major problem in the field of automatic control . For time-delay systems , The most important thing is to control , The control of time-delay characteristics is very common . In the development of time-delay system control , There is Smith Predictive control 、 Dahlin algorithm 、 Adaptive control 、 Predictive control 、 Application of various control methods such as variable structure control and intelligent controller in time-delay systems , The advantages and disadvantages of these methods are summarized , It is concluded that compound control is an effective and practical method to control time-delay systems , And it has great application prospects . thus it can be seen , The importance of time-delay systems is self-evident , What we are going to study is how to solve the stability problem of time-delay systems , How to achieve good control effect .
Lambert W Function is also called Omega function or multiplier logarithm , It is a multivalued function , There are infinite branches , And every branch is a single valued function , In the range of real numbers, there are W(x0) and W(x1) Two , The former is called Lambert W The main branch of the function .Lambert W The function is also f(W)=Wexp(W) The inverse function of ,exp(W) It's an exponential function ,W Is any plural . all the time , Scholars at home and abroad have also made some research on this function . In the first , Just use it to solve some basic mathematical problems , For example, the equation with exponent , Delay differential equations , Calculation of trees in Combinatorial Mathematics . and , With the in-depth study of this function , Found more uses for it , From mathematics to physics 、 chemical 、 In biology and other fields , Such as in Quantum Chemistry , Some problems in statistical mechanics use W Function to solve . Especially some complicated problems , application Lamberr W Function representation is much more convenient , Some equation solutions can be expressed by it , Coupled with the current development of related mathematical software, such as Matlab,Maple etc. , Provide corresponding function calculation Lambert W function , It is possible to calculate the solutions of these equations with high accuracy , It also provides convenience for studying the stability of time-delay systems .
3、 Simulation analysis
clc
close all
clear
%% First order
tao = 1;
Kp = -2;
k = -4:4;
alpha = 1;
for i = 1:length(k)
x = -Kp*tao*exp(tao*alpha);
y = lambertw(k(i),x);
s(i) = y/tao-alpha;
end
figure
plot(real(s),imag(s),'marker','.','markersize',18,'color','black')
xlabel Real component
ylabel Imaginary part
set(gcf,'color','w');
%% Second order
% -------------- Kp = -2 ------------------------------
n = 2;
Kp = -2;
alpha = 1;
tao = 1;
k = -4:4;
l = 0;
for i = 1:length(k)
if Kp<0
x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*2*l*pi/n);
y = lambertw(k(i),x);
s0(i) = n/tao*y-alpha;
else
x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*(2*l+1)*pi/n);
y = lambertw(k(i),x);
s0(i) = n/tao*y-alpha;
end
end
l = 1;
for i = 1:length(k)
if Kp<0
x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*2*l*pi/n);
y = lambertw(k(i),x);
s1(i) = n/tao*y-alpha;
else
x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*(2*l+1)*pi/n);
y = lambertw(k(i),x);
s1(i) = n/tao*y-alpha;
end
end
figure
plot(real(s0),imag(s0),'marker','.','markersize',18,'color','red')
hold on
plot(real(s1),imag(s1),'marker','.','markersize',18,'color','black')
hold off
xlabel Real component
ylabel Imaginary part
set(gcf,'color','w');
% -------------- Kp = 2 ------------------------------
n = 2;
Kp = 2;
alpha = 1;
tao = 1;
k = -4:4;
l = 0;
for i = 1:length(k)
if Kp<0
x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*2*l*pi/n);
y = lambertw(k(i),x);
s0(i) = n/tao*y-alpha;
else
x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*(2*l+1)*pi/n);
y = lambertw(k(i),x);
s0(i) = n/tao*y-alpha;
end
end
l = 1;
for i = 1:length(k)
if Kp<0
x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*2*l*pi/n);
y = lambertw(k(i),x);
s1(i) = n/tao*y-alpha;
else
x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*(2*l+1)*pi/n);
y = lambertw(k(i),x);
s1(i) = n/tao*y-alpha;
end
end
figure
plot(real(s0),imag(s0),'marker','.','markersize',18,'color','red')
hold on
plot(real(s1),imag(s1),'marker','.','markersize',18,'color','black')
hold off
xlabel Real component
ylabel Imaginary part
set(gcf,'color','w');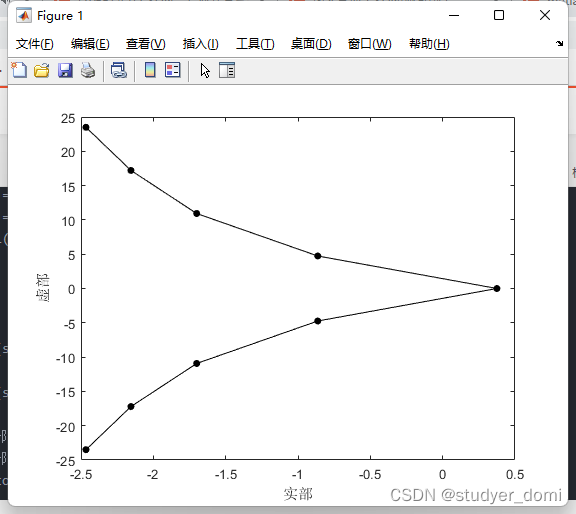

4、 Reference paper
边栏推荐
- 2022 RoboCom 世界机器人开发者大赛-本科组(省赛)-- 第三题 跑团机器人 (已完结)
- 【机器学习基础】——另一个视角解释SVM
- Kubectl_好用的命令行工具:oh-my-zsh_技巧和窍门
- JSON file editor
- Chiitoitsu
- DS binary tree - maximum distance of binary tree nodes
- Tiger mouth waterfall: Tongliang version of xiaohukou waterfall
- Use of keywords const, volatile and pointer; Assembly language and view of register status
- Conflict resolution of onblur and onchange
- 【量化测试】
猜你喜欢
Explain the edge cloud in simple terms | 2. architecture

27. Directory and file system

Huawei camera capability
DS binary tree - parent and child nodes of binary tree

【量化测试】

Existence form and legitimacy of real data in C language (floating point number)
ZABBIX administrator forgot login password

力扣 31.下一个排列--双指针法

(零九)Flask有手就行——Cookie和Session

Activity Registration: how to quickly start the open source tapdata live data platform on a zero basis?
随机推荐
【OpenCV 例程300篇】238. OpenCV 中的 Harris 角点检测
Sword finger offer II 001. integer division
哈夫曼树(最优二叉树)
C# - partial 关键字
Tiger mouth waterfall: Tongliang version of xiaohukou waterfall
24.原生磁盘的使用
Huffman tree (optimal binary tree)
力扣 31.下一个排列--双指针法
[300 opencv routines] 238. Harris corner detection in opencv
The first n rows sorted after dataframe grouping nlargest argmax idmax tail!!!!
《Route planning method for UAV in unknown environment based on improved SAS algorithm》翻译
C# SQLite Database Locked exception
华为相机能力
2022 RoboCom 世界机器人开发者大赛-本科组(省赛)-- 第五题 树与二分图 (已完结)
图的存储和遍历
Leetcode-09 (next rank + happy number + full rank)
PrestoUserError: PrestoUserError(type=USER_ERROR, name=INVALID_FUNCTION_ARGUMENT, message=“Escape st
Mysql库的操作
Chiitoitsu
[quantitative test]
