当前位置:网站首页>AtCoder Beginner Contest 262 D - I Hate Non-integer Number
AtCoder Beginner Contest 262 D - I Hate Non-integer Number
2022-08-04 21:08:00 【Vegetable newbie】
AtCoder Beginner Contest 262
D - I Hate Non-integer Number
题意
给你一个长度为 n n n的数组,问:从数组中选择任意个 元素,这些元素的平均数为整数的方案数为多少。
数据范围
1 ⩽ n ⩽ 100 1 \leqslant n \leqslant 100 1⩽n⩽100
思路
本题考察 动态规划
我们令 d p [ j ] [ k ] [ l ] dp[j][k][l] dp[j][k][l]为在长度为 i i i的情况下,数组中前 j j j个元素中选择 k k k个元素 m o d mod mod % i \%i %i 为 l l l的方案数。
那么答案就是
∑ i = 1 n d p [ n ] [ i ] [ 0 ] \sum_{i = 1}^{n} dp[n][i][0] i=1∑ndp[n][i][0]
转移:我们可以考虑第 j j j个数是否选择来进行转移
d p [ j ] [ k ] [ l ] = { d p [ j − 1 ] [ k ] [ l ] ( 不选 ) d p [ j − 1 ] [ k − 1 ] [ l − ( a [ j ] % i ) ] ( a [ j ] % i ⩾ 0 ) d p [ j − 1 ] [ k − 1 ] [ i + l − ( a [ j ] % i ) ] ( a [ j ] % i < 0 ) dp[j][k][l] = \begin{cases}dp[j - 1][k][l]\quad(不选)\\ dp[j - 1][k - 1][l - (a[j]\ \% \ i)] \quad(a[j] \ \%\ i\ \geqslant\ 0)\\ dp[j - 1][k - 1][i + l - (a[j] \ \% \ i)]\quad (a[j]\ \% \ i< 0)\end{cases} dp[j][k][l]=⎩⎨⎧dp[j−1][k][l](不选)dp[j−1][k−1][l−(a[j] % i)](a[j] % i ⩾ 0)dp[j−1][k−1][i+l−(a[j] % i)](a[j] % i<0)
初始化:
d p [ 0 ] [ 0 ] [ 0 ] = 1 dp[0][0][0] = 1 dp[0][0][0]=1
时间复杂度
O ( N 4 ) O(N^4) O(N4)
代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define LL long long
#define fi first
#define se second
#define debug(a) cout<<#a<<"="<<a<<endl;
#define all(x) (x).begin(),(x).end()
#define pb push_back
#define Yes puts("Yes");
#define No puts("No");
#define sz(x) (int)x.size()
using namespace std;
inline string rd()
{
string str="";
char ch=getchar();
while(ch==' ' || ch=='\n' || ch=='\r')
{
ch=getchar();
}
while(ch!=' ' && ch!='\n' && ch!='\r')
{
str+=ch;
ch=getchar();
}
return str;
}
inline void print(string s)
{
for(int i=0; s[i]!='\0'; i++) putchar(s[i]);
}
template <typename T> void read(T &t) {
t=0; char ch=getchar(); int f=1;
while (ch<'0'||ch>'9') {
if (ch=='-') f=-1; ch=getchar(); }
do {
(t*=10)+=ch-'0'; ch=getchar(); } while ('0'<=ch&&ch<='9'); t*=f;
}
template <typename T> void write(T t) {
if (t<0) {
putchar('-'); write(-t); return; }
if (t>9) write(t/10);
putchar('0'+t%10);
}
template <typename T> void writeln(T t) {
write(t); puts(""); }
const int N = 110, mod = 998244353;
int a[N], n;
LL dp[N][N][N];//dp[j][k][l]表示前j个数选则k个数的和modi为l的方案数
int main()
{
read(n);
LL sum = 0;
for(int i = 1; i <= n; i ++ ) read(a[i]);
for(int i = 1; i <= n; i ++ ){
//一共选i个数 O(N^4)
dp[0][0][0] = 1;
for(int j = 1; j <= n; j ++ ){
for(int k = 0; k <= j; k ++ ){
for(int l = 0; l < i; l ++ ){
// 不选的方案数
dp[j][k][l] = (dp[j][k][l] + dp[j - 1][k][l]) % mod;
// 选的方案数
int x = a[j] % i;
if(k >= 1){
if(l - x >= 0) dp[j][k][l] = (dp[j][k][l] + dp[j - 1][k - 1][l - x]) % mod;
else dp[j][k][l] = (dp[j][k][l] + dp[j - 1][k - 1][i + l - x]) % mod;
}
}
}
}
sum += dp[n][i][0];
sum %= mod;
memset(dp, 0, sizeof dp);
}
printf("%lld\n",sum);
return 0;
}
边栏推荐
- dotnet 通过 WMI 获取系统安装软件
- js的new Function()常用方法
- dotnet delete read-only files
- Common methods of js's new Function()
- 帝国CMS仿核弹头H5小游戏模板/92game帝国CMS内核仿游戏网整站源码
- 88.(cesium之家)cesium聚合图
- LayaBox---TypeScript---Problems encountered at first contact
- proe和creo的区别有哪些
- [2022 Nioke Duo School 5 A Question Don't Starve] DP
- 数字IC设计中基本运算的粗略的延时估计
猜你喜欢

数电快速入门(二)(复合逻辑运算和逻辑代数的基本定律的介绍)

如何用好建造者模式

js数据类型、节流/防抖、点击事件委派优化、过渡动画
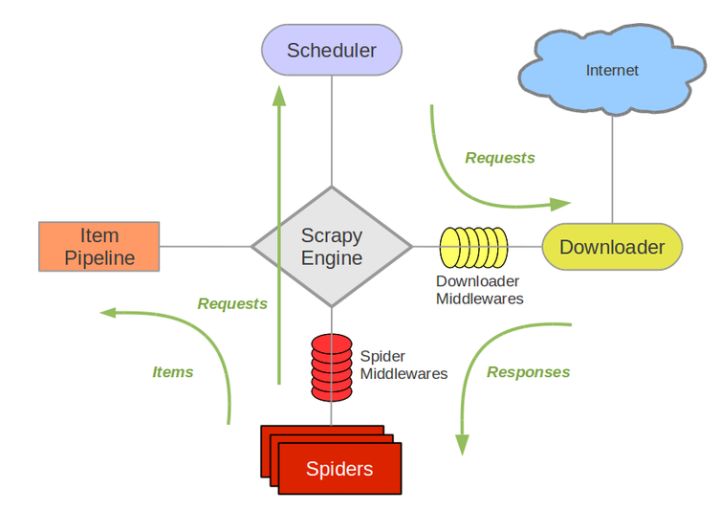
如何最简单、通俗地理解爬虫的Scrapy框架?
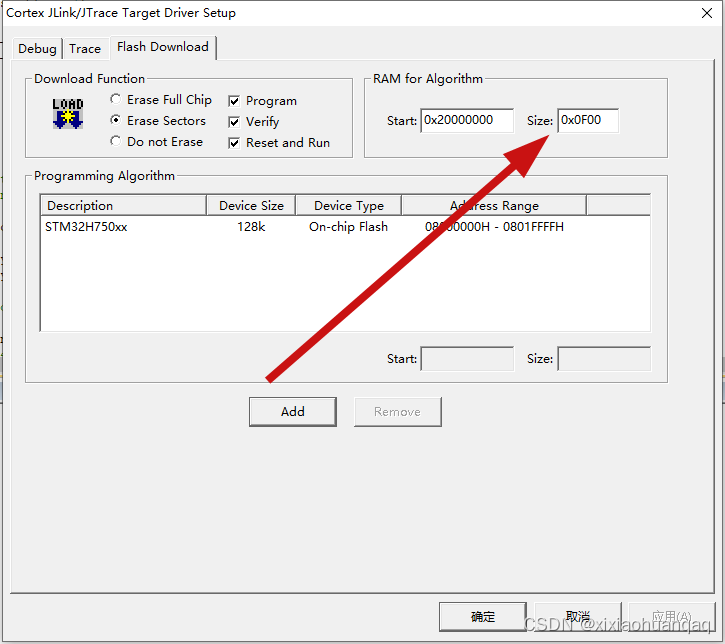
mdk5.14无法烧录

Configure laravel queue method using fort app manager

Zynq Fpga图像处理之AXI接口应用——axi_lite接口使用

Oreo domain name authorization verification system v1.0.6 public open source version website source code

Interviewer: How is the expired key in Redis deleted?

88. (the home of cesium) cesium polymerization figure
随机推荐
Data warehouse (1) What is data warehouse and what are the characteristics of data warehouse
大资本已开始逃离加密领域?
LayaBox---TypeScript---举例
OD-Model【6】:YOLOv2
链路聚合技术及VRRP
dotnet 使用 lz4net 压缩 Stream 或文件
3、IO流之字节流和字符流
ini怎么使用? C#教程
后缀式的计算
dotnet compress Stream or file using lz4net
PyTorch Geometric (PyG) 安装教程
宝塔实测-搭建中小型民宿酒店管理源码
【数据挖掘】搜狐公司数据挖掘工程师笔试题
mdk5.14无法烧录
How to train a deep learning model?
adb shell input keyevent 模拟按键事件
Retrofit的使用及原理详解
【2022杭电多校5 1012题 Buy Figurines】STL的运用
暴雨中的人
[2022 Hangzhou Electric Multi-School 5 1003 Slipper] Multiple Super Source Points + Shortest Path