Traversal of binary tree and related knowledge

---

1. Recursive traversal

1.1 The former sequence traversal

vector<int> res;
vector<int> PreTravelsal(vector<int> res, TreeNode* root)
{
    
	res.clear();
	travelsal(root);
	return res;	
}
void travelsal(TreeNode* cur)
{
    
	if(cur == NULL) return;
	res.push_back(cur->val);
	travelsal(cur->left);
	travelsal(cur->right);
}

1.2 In the sequence traversal

vector<int> res;
vector<int> PreTravelsal(vector<int> res, TreeNode* root)
{
    
	res.clear();
	travelsal(root);
	return res;	
}
void travelsal(TreeNode* cur)
{
    
	if(cur == NULL) return;
	res.push_back(cur->val);
	//travelsal(cur->left);
	res.push_back(cur->val);
	travelsal(cur->right);
}

1.3 After the sequence traversal

vector<int> res;
vector<int> PreTravelsal(vector<int> res, TreeNode* root)
{
    
	res.clear();
	travelsal(root);
	return res;	
}
void travelsal(TreeNode* cur)
{
    
	if(cur == NULL) return;
	//res.push_back(cur->val);
	travelsal(cur->left);
	travelsal(cur->right);
	res.push_back(cur->val);
}

2. Iterate through

2.1 The former sequence traversal

vector<int> travelsal(TreeNode* root)
{
    
	vector<int> res;
	stack<TreeNode*> st;
	if(root == NULL) return res;
	st.push(root);
	while(!st.empty())
	{
    
		TreeNode* cur = st.top();
		st.pop();
		res.push_back(cur->val);
		if(cur->right) st.push(cur->right);
		if(cur->left) st.push(cur->left);
	}
	return res;
}

2.2 After the sequence traversal

vector<int> travelsal(TreeNode* root)
{
    
	vector<int> res;
	stack<TreeNode*> st;
	if(root == NULL) return res;
	st.push(root);
	while(!st.empty())
	{
    
		TreeNode* cur = st.top();
		st.pop();
		res.push_back(cur->val);
		if(cur->left) st.push(cur->left);
		if(cur->right) st.push(cur->right);
	}
	reverse(res.begin(), res.end());
	return res;
}

2.3 In the sequence traversal

vector<int> travelsal(TreeNode* root)
{
    
	vector<int> res;
	stack<TreeNode*> st;
	TreeNode* cur = root;
	while(cur != NULL || !st.empty())
	{
    
		if(cur != NULL)
		{
    
			st.push(cur);
			cur = cur->left;
		}
		else
		{
    
			cur = st.top();
			st.pop();
			res.push_back(cur->val);
			cur = cur->right;
		}
	}
	return res;

3. Sequence traversal

vector<int> travelsal(TreeNode* root)
{
    
	vector<int> res;
	queue<TreeNode*> que;
	if(root == NULL) return res;
	que.push(root);
	while(!que.empty())
	{
    
		int n = que.size();
		for(int i = 0; i < n; i++)
		{
    
			TreeNode* cur = que.front();
			que.pop();
			res.push_back(cur->val);
			if(cur->left) que.push(cur->left);
			if(cur->right) que.push(cur->right);
		}
	}
	return res;
}

4. The species of binary trees

1. Perfect binary tree ： A binary tree has only a degree of 0 The node and degree of are 2 The node of , And the degree is 0 On the same layer , Its depth is k, The number of nodes is 2^k-1;
2. Perfect binary tree ： In a complete binary tree , Except that the lowest node may not be full , The number of nodes in each layer reaches the maximum , And the nodes of the lowest layer are concentrated in the leftmost positions of the layer . If the bottom layer is No h layer , Then the layer contains 1~ 2^(h-1) Nodes .
   
3. Binary search tree ： If its left subtree is not empty , Then the value of all nodes in the left subtree is less than the value of its root node ; If its right subtree is not empty , Then the value of all nodes in the right subtree is greater than the value of its root node ; Its left 、 The right subtree is also a binary sort tree .
   
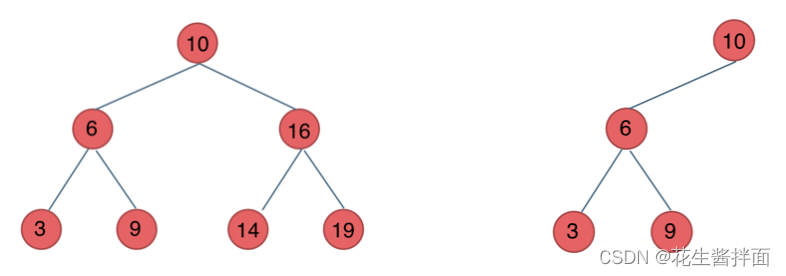
   4. Balanced binary search trees ： Also known as AVL（Adelson-Velsky and Landis） Trees , And has the following properties ： It is an empty tree or the absolute value of the height difference between its left and right subtrees does not exceed 1, And both the left and right subtrees are a balanced binary tree .