Dynamic planning 111

Basic questions

1. knapsack problem ( Restricted fetch set , Seeking value or variety )
2. raid homes and plunder houses
3. Stock issues
4. Subsequence problem

Basic solution

1. dp Array , And the meaning of subscript
2. The recursive formula
3. dp Array initialization
4. traversal order （ One dimensional array layer , Two-dimensional array two layers ）

   1. If you find the combination number, it's the outer layer for Loop through items , Inner layer for Traverse the backpack .

      If you find the permutation number, it's the outer layer for Traverse the backpack , Inner layer for Loop through items .

   2. if 01 knapsack , From the back to the front , Otherwise, from front to back

5. Print array （debug）

Ideas :

The key is to think from the bottom up

First consider step ,

For example, the backpack problem , The steps are to put items one by one , How to put items is the optimal solution . There are two steps for each item , Don't put . Observe the overall situation and decide whether to put it or not .（ Step back from your head to see if you want to put ）

Another example is going up the steps , Step is step , Taking a few steps is the optimal solution , You can take one or two steps at a time . Observe the overall situation and decide whether to take one step or two .（ Step back from your head , Is it one-step optimal or two-step optimal each time ）

Every step-by-step problem , The next state has a problem that depends on the previous state. Consider using dynamic programming . Start with the last step , Imagine what operations are required for the state from the last step to the end

The value of dynamic programming array must be the answer

knapsack problem ( Seeking value )

It is a set of values with limits and values . The capacity of the backpack and the weight of the items constitute a limitation , The value of the goods is the value .

Two dimensional writing ：

// 1 dp Array subscript and its meaning 
    // dp[i][j]
    //i: from 0 -i Item No  j： Backpack Capacity 
    //ij: from 0-i Take whatever you like , Put in j The greatest value in 
// 2  The recursive formula 
    // dp[i][j]=max(dp[i-1][j],dp[i-1][j-w]+value)
// 3 dp Array initialization 
    // Physical truth 
// 4  traversal order 
    // First pack your stuff 


    // 
function bagProblem(weight,value,volume){
    let count=weight.size+1
    // 1  Definition dp
    const dp=[]

    // 3  initialization dp Array 
    for (let j = volume; j >= weight[0]; j--) {
        dp[0][j] = dp[0][j - weight[0]] + value[0];
    }


    // 4  traversal order 
    for(let i=1;i<weight.length;i++){
        for(let j=0;j<=volume;j++){
            if(j<weight[i]){
                dp[i][j]=dp[i-1][j]
            }else{
                // 2  The recursive formula 
                dp[i][j]=max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
            }
        }
    }
}

Compress , One dimensional writing

From the picture above, we can get dp[i][j] Partly by dp[i-1][j] Copy it , Space can be omitted completely , Replace with a one-dimensional array

1、dp Definition

In one dimension dp Array ,dp[j] Express ： Capacity of j The backpack , The value of the items carried can be up to dp[j].

2、 The recursive formula

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

here dp[j] There are two choices , One is to take yourself dp[j], One is to take dp[j - weight[i]] + value[i], Specify the maximum , After all, it's for maximum value ,

3、dp Array initialization

Initialize to 0

4、 traversal order

Cycle back and forth , Each acquisition state will not coincide with the previous acquisition state , So each item can only be taken once .

For two dimensions dp,dp[i][j] All through the upper layer, that is dp[i - 1][j] Come by calculation , On this floor dp[i][j] Not covered ！

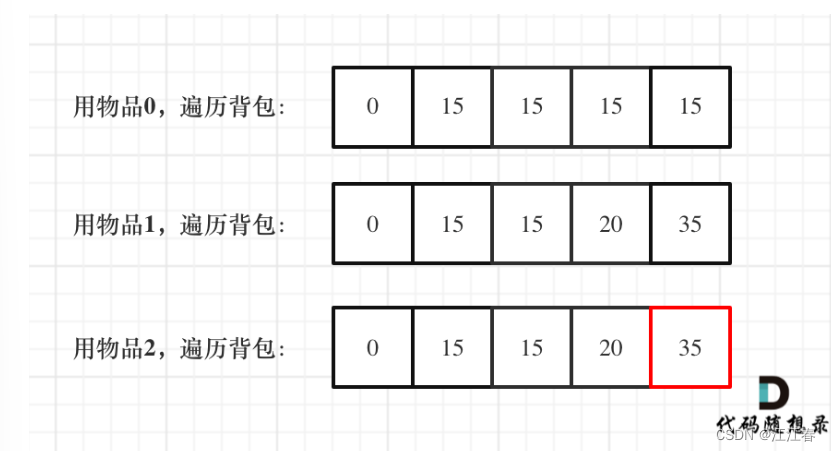
for(int i = 0; i < weight.size(); i++) { //  Traverse the items
    for(int j = bagWeight; j >= weight[i]; j--) { //  Traverse the backpack capacity
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

// 1 dp Array subscript and its meaning 
    // dp[j]: Capacity of j The greatest value of time 
    //j: Capacity 
// 2  The recursive formula 
    // dp[j]=max(dp[j],dp[j-w[i]]+value)
    //  there dp[j] In fact, it is a copy of the upper layer in a two-dimensional array , That is, the value of the previous item when it is not put 
// 3 dp Array initialization 
    // All for 0
// 4  traversal order 
    // First pack your stuff 
    //  Traverse the knapsack in reverse order , Prevent the upper state from being overwritten 


function bagProblem(weight,value,volume){
    let count=weight.size
    // 1  Definition dp
    const dp=[]

    // 3  initialization dp Array 
    // 
    for(let i=0;i<volume;i++){
        dp[i]=0
    }

    // 4  traversal order 
    for(let i=0;i<weight.length;i++){
        // ps： Greater than weight, Less than weight You can't directly put it in and inherit the state of the previous level （ Not put directly ）
        for(let j=volume;j>=weight[i];j--){
            // 2  Recursive formula 
            dp[j]=max(dp[j],dp[j-weight[i]]+value[i])
        }
    }
}

  Full backpack problem

Combination question

Topic link ：https://leetcode-cn.com/problems/target-sum/

difficulty ： secondary

Given an array of nonnegative integers ,a1, a2, ..., an, And a target number ,S. Now you have two symbols  +  and  -. For any integer in the array , You can go from  +  or  - Select a symbol to add to the front .

Return can make the final array and the target number S Of all methods to add symbols .

Limit ：

  left = (target + sum)/2 .

step

1. determine dp The meaning of arrays and subscripts

dp[j] Express ： fill j（ Include j） Such a large volume bag , Yes dp[i] Methods

In fact, you can also use two-dimensional dp Array to solve the problem ,dp[i][j]： Use Subscript to be [0, i] Of nums[i] Can fill up j（ Include j） Such a large bag , Yes dp[i][j] Methods .

     2、 The recursive formula

Don't consider nums[i] Under the circumstances , The filling capacity is j - nums[i] The backpack , Yes dp[j - nums[i]] Medium method .

So just get nums[i] Words , manage to put together dp[j] There is dp[j - nums[i]] Methods .

For example ,nums[i] = 2：dp[3], The capacity of the filled backpack is 3 Words , Yes dp[3] Methods .

Then you just need to get one 2（nums[i]）, Yes dp[3] Method can aggregate a capacity of 3 The backpack , Correspondingly, there are many ways to gather the capacity of 5 The backpack .

So you need to take These methods add up ,dp[i] += dp[j - nums[j]

        3、dp How to initialize an array

As can be seen from the recursive formula , At initialization time dp[0] Be sure to initialize to 1, because dp[0] Is the origin of all recursive results in the formula , If dp[0] yes 0 Words , The recursive result will be 0.

dp[0] = 1, It's also easy to explain in theory , The full capacity is 0 The backpack , Yes 1 Methods , It's just pretend 0 Item .

dp[j] The values corresponding to other subscripts should be initialized to 0, It can also be seen from the recursive formula ,dp[j] Make sure it's 0 The initial value of the , In order to correctly by dp[j - nums[i]] derived .

        4、 traversal order

01 Knapsack problem dp The traversal ,nums Put it in the outer loop ,target Cycle, , And the internal circulation is reversed .

Recurrence formulas of several knapsacks

Ask if you can fill your backpack （ Or how much at most ）：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); , The corresponding topics are as follows ：

• Dynamic programming ：416. To divide into equal and subsets

• Dynamic programming ：1049. The weight of the last stone II

There are several ways to fill a backpack ：dp[j] += dp[j - nums[i]] , The corresponding topics are as follows ：

• Dynamic programming ：494. Objectives and

• Dynamic programming ：518. Change for II

• Dynamic programming ：377. Combinatorial summation Ⅳ

• Dynamic programming ：70. Stair climbing advanced version （ Completely backpack ）

Ask if the back package is full of maximum value ：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); , The corresponding topics are as follows ：

• Dynamic programming ：474. One and zero

Ask the minimum number of all items in a full backpack ：dp[j] =  min(dp[j - coins[i]] + 1, dp[j]); , The corresponding topics are as follows ：

• Dynamic programming ：322. Change for

• Dynamic programming ：279. Complete square

---

raid homes and plunder houses