当前位置:网站首页>Count the logarithm of points that cannot reach each other in an undirected graph [classic adjacency table building +dfs Statistics - > query set optimization] [query set manual / write details]
Count the logarithm of points that cannot reach each other in an undirected graph [classic adjacency table building +dfs Statistics - > query set optimization] [query set manual / write details]
2022-06-27 00:56:00 【REN_ Linsen】
Classic adjacency table +DFS Statistics -> And look up set optimization
Preface
Given nodes and edges ( Node pair ), Find the connected components and their variants . The first idea is based on nodes and node pairs ( edge ) To establish adjacency matrix , stay DFS To do things .
But there is also an idea closely related to connected components , Union checking set , It does not create a complete graph , But can do the corresponding thing , So the running time is short .
It takes the original graph , Select a node as the root node , All direct / Indirectly connected nodes act as child nodes , Can solve many connected components / Connected component variation problem .
In addition to the above advantages , I feel its array hash Than hashMap fast , After all, the array is JVM level , And continuous inner layer distribution , Than API fast .
One 、 Count the logarithm of points that cannot reach each other in an undirected graph


Two 、 Classic adjacency table +DFS Statistics -> And look up set optimization
1、 Classic adjacency table +DFS Statistics
public class CountPairs {
public long countPairs(int n, int[][] edges) {
// Join all nodes .
for (int i = 0; i < n; i++) addNode(i);
for (int[] edge : edges) addEdge(edge[0], edge[1]);
List<Long> arr = new ArrayList<>();
for (int i = 0; i < n; i++) if (graph.containsKey(i)) arr.add(dfs(i));
//
long[] prefix = new long[arr.size()];
long sum = 0, ans = 0;
int idx = 0;
for (long i : arr) prefix[idx++] = (sum += i);
for (int i = 0; i < arr.size() - 1; i++) ans += arr.get(i) * (prefix[arr.size() - 1] - prefix[i]);
return ans;
}
private long dfs(int n) {
long rs = 1;
Set<Integer> next = graph.get(n);
if (next == null) return rs;
graph.remove(n);
for (Integer i : next) {
if (graph.containsKey(i)) rs += dfs(i);
}
return rs;
}
private void addEdge(int a, int b) {
addNode(a);
addNode(b);
graph.get(a).add(b);
graph.get(b).add(a);
}
private void addNode(int b) {
if (!graph.containsKey(b)) graph.put(b, new HashSet<>());
}
Map<Integer, Set<Integer>> graph = new HashMap<>();
}
2、 And look up set optimization
// Practice hashing , It is a sharp weapon about connected components .
class CountPairs2 {
public long countPairs(int n, int[][] edges) {
// And the first step of the search set standard : initialization .
int[] father = new int[n];
Arrays.fill(father, -1);
// And the second step of the search set standard :union
cnt = n;// Here, I want to count the number of connected components , The number of nodes of each connected component will be counted , You can use arrays , Not expandable list.| Or directly list
for (int[] edge : edges) union(father, edge[0], edge[1]);
// Nonspecific logic , The specific requirements shall be specified .
// Count the number of nodes of each connected component .
int[] arr = new int[cnt];
cnt = 0;
for (int f : father) if (f < 0) arr[cnt++] = -f;
// Nonspecific logic , The specific requirements shall be specified .
// Get the number of nodes with different connected components , Use prefixes and , Space for time .
long[] prefix = new long[arr.length];
long sum = 0;
cnt = 0;
for (int a : arr) prefix[cnt++] = (sum += a);
// Get the results
long ans = 0;
for (int i = 0; i < arr.length - 1; i++) ans += arr[i] * (prefix[prefix.length - 1] - prefix[i]);
return ans;
}
int cnt = 0;// The number of connected components .
private void union(int[] father, int m, int n) {
// And the third step of the search set standard :findFather
int r1 = findFather(father, m);
int r2 = findFather(father, n);
// Not the same logic , Write according to the actual situation .
if (r1 != r2) {
// Combine the two , Just take one as the root , Get the number of nodes of the whole tree , A negative number here means .
father[r1] += father[r2];
// And take the other as a subtree , And modify its root node .
father[r2] = r1;
// Optional operation , When used list when , Are not .
--cnt;
}
}
private int findFather(int[] father, int r) {
// All the way back to the root , And take the root as the root of each node on the path .
// Embodied in if (father[r] != r) father[r] = findFather(father, father[r]); return father[r]; This will tile the deep trees .
// But not here , Because the value of the root node is not equal to its subscript , It's a negative number , Count the number of nodes .
// There is a need to change the traditional practice , Be flexible .
// If the node is the root
if (father[r] < 0) return r;
return father[r] = findFather(father, father[r]);
}
}
summary
1) Classic adjacency table establishment + stay dfs Traverse ( Figure basis of operation ) Do your own thing .
2) And look up the set to change the shape of the graph , But it does not affect problem solving , Then its reduced running time becomes an advantage .
3) In addition to the above advantages , I feel its array hash Than hashMap fast , After all, the array is JVM level , And continuous inner layer distribution , Than API fast .
4) And the classic three steps of searching sets , Each step can be based on specific needs , And flexible writing . The specific three steps are : Initialize array father[size]{}( Array hash very nice)、union(int[],int,int) Connect two nodes 、findFather(int[],int) Find the root node .
reference
[1] LeetCode Count the logarithm of points that cannot reach each other in an undirected graph
边栏推荐
- Great health industry annual must attend event, 2022 Shandong International Great Health Industry Expo
- Lorsque le transformateur rencontre l'équation différentielle partielle
- One click acceleration of Sony camera SD card file copy operation, file operation batch processing tutorial
- 论文解读(LG2AR)《Learning Graph Augmentations to Learn Graph Representations》
- Concepts de base de données Oracle
- The [MySQL] time field is set to the current time by default
- CPU exception handling
- Play OLED, u8g2 animation, increasing numbers, random triangles, etc
- 當Transformer遇見偏微分方程求解
- Other service registration and discovery
猜你喜欢

Other service registration and discovery
![[UVM actual battle== > episode_3] ~ assertion, sequence, property](/img/78/7ce3a9a4e933a58f90478be53e6e61.png)
[UVM actual battle== > episode_3] ~ assertion, sequence, property

Statistical Hypothesis Testing

當Transformer遇見偏微分方程求解

com. fasterxml. jackson. databind. exc.MismatchedInputException: Expected array or string. at [Source:x

Simple and fast digital network (network dolls in the network)

史上最难618,TCL夺得电视行业京东和天猫份额双第一
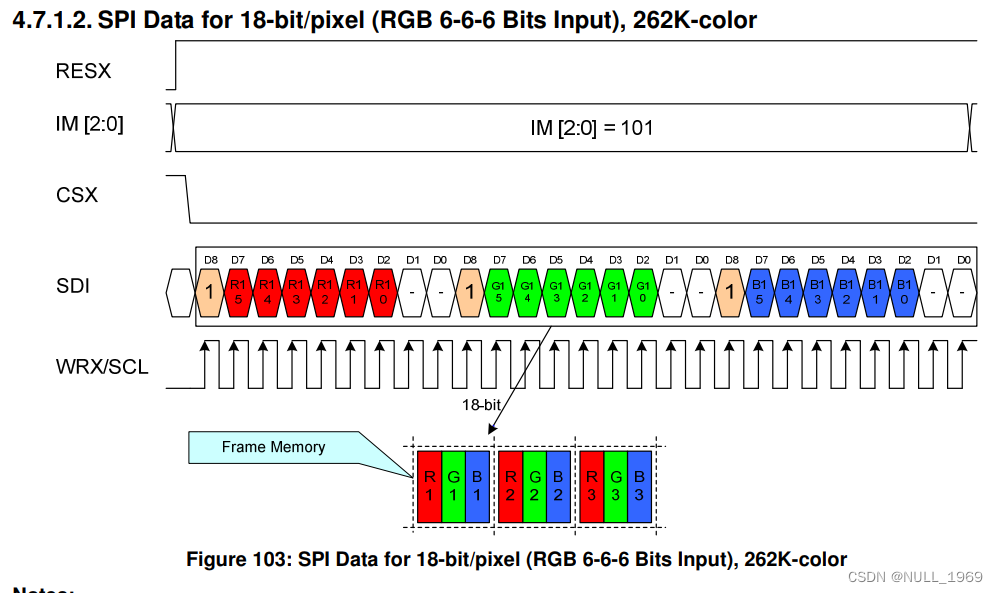
3线spi屏幕驱动方式

Sword finger offer 10- ii Frog jumping on steps

3-wire SPI screen driving mode
随机推荐
memcached基础1
Oracle database basics concepts
数据库面试题+sql语句解析
如何把老式键盘转换成USB键盘并且自己编程?
3 - wire SPI Screen Drive
Mindspire, a domestic framework, cooperates with Shanshui nature conservation center to find and protect the treasure life in the "China water tower"
MATLAB data type - character type
[UVM actual battle== > episode_3] ~ assertion, sequence, property
How to control the quality of HD slip ring in the production process
TopoLVM: 基于LVM的Kubernetes本地持久化方案,容量感知,动态创建PV,轻松使用本地磁盘
Solution of idea hot start failure
2022年地理信息系统与遥感专业就业前景与升学高校排名选择
At present, which securities company is the best and safest to open an account for stock speculation?
Statistical Hypothesis Testing
Pet hospital management system based on SSMP
Timing mechanism of LwIP
超越锂电池——未来电池的概念
About Random Numbers
根据文件名批量生成文件夹
Play OLED, u8g2 animation, increasing numbers, random triangles, etc