当前位置:网站首页>A Dynamic Near-Optimal Algorithm for Online Linear Programming
A Dynamic Near-Optimal Algorithm for Online Linear Programming
2022-06-22 20:37:00 【ZZZZZ Zhongjie】
The natural optimization model for many online resource allocation problems is online linear programming (LP) problem , The constraint matrix is displayed column by column together with the corresponding target coefficients .
In such a model , A decision variable must be set each time a column is displayed , Without looking at future input , The goal is to maximize the overall objective function . In this paper , We are in random order of arrival and LP The right input size is assumed under some mild conditions , An approximate optimal algorithm is proposed for this kind of general online problems . say concretely , Our learning based algorithm works by dynamically updating the threshold price vector at geometric intervals , The double price learned from the column displayed in the previous period is used to determine the sequence decision of the current period . Through dynamic learning , The competitiveness of our algorithm is higher than that of previous studies on the same problem . We also provide a worst-case example , It shows that the performance of our algorithm is close to the best .
Subject classification : Online algorithms ; Linear programming ; Primal duality ; Dynamic price update .
1 Introduce
Online optimization in computer science 、 Operations research and management science have attracted more and more attention . In many practical problems , The data is not exposed at the beginning , But in an online way . for example , In online revenue management , Consumers arrive in order , Everyone asks for a subset of products ( for example , Multiple flights or staying in a hotel for a while ) And provide the bid price . On request , The Seller shall make an irrevocable decision on whether to accept or reject the bid , The overall goal is to maximize revenue while meeting resource constraints .
Similarly , In the online routing problem , The network capacity manager receives a series of requests from users , These requests have the intended use of the network , Each request has a specific utility .
His goal is to allocate network capacity to maximize social welfare . A similar format also appears in online auctions 、 Online keyword matching problem 、 Online packaging and various other online revenue management and resource allocation problems . Overview of online optimization literature and its recent development , We ask readers to refer to Borodin and El-Yaniv (1998)、Buchbinder and Naor (2009a) as well as Devanur (2011).
In the example above , The problem can be expressed as online linear programming (LP) problem .
( Sometimes , People will consider the corresponding integer programming . Although our discussion focuses on the LP Relax , But our results naturally extend to integer programming . A discussion about this , Please refer to No 5.2 section .) On-line LP The problem takes linear programming as its Basic form , The constraint matrix and the corresponding coefficients in the objective function are displayed column by column . Observe the input , A decision must be made immediately , Without looking at future data . To be exact , Let's consider the following ( offline ) Linear program :
(1)
On-line LP The goal of the problem is to choose xt Make the objective function Pn t=1 txt Maximize .
In this paper , We propose to solve the online problem LP A good algorithm for the problem . To define the performance of the algorithm , We first need to make some assumptions about the input parameters . We use the following random permutation model in this paper : hypothesis 1. Column aj( With target coefficient j) Arrive in random order . Line up 4a1 1 a2 10 0 01 and 5 Can be disadvantageously chosen at the beginning . however ,4a1 1 a2 10 0 01 and 5 The arrival order of is evenly distributed over all permutations .
hypothesis 2. We know the total number of columns a priori n.
The random permutation model is used in many existing literatures of online problems ( A comprehensive review of relevant literature , Please refer to No 1.3 section ). It is an intermediate path between using the worst-case analysis and assuming that the input distribution is known . A completely robust worst-case analysis with input uncertainty evaluates the algorithm based on its performance on the worst-case input ( for example , See Mehta wait forsomeone 2005,Buchbinder and Naor 2009b). However , This leads to very pessimistic performance bounds for this problem : No online algorithm can achieve better than the optimal offline solution O41/n5 Approximation is better (Babaioff et al. 2008). by comparison , Although the prior input distribution can greatly simplify the problem , But the choice of distribution is crucial , If the actual input distribution is not consistent with the assumption , Performance will be affected . say concretely , hypothesis 1 The ratio assumes that the column is independent of some ( May be unknown ) The distribution plot should be weak . in fact , People can see n.i.d. Columns are first extracted from the underlying distribution n Samples , Then arrange them randomly . therefore , If the input data is i.i.d Draw the , Our proposed algorithm and its performance will also be applicable . From some distribution .
hypothesis 2 It's necessary , Because we need to use quantity n To determine the historical length of the learning threshold price in our algorithm . in fact , Such as Devanur and Hayes (2009) Shown , Any algorithm must achieve near optimal performance .2 However , This assumption can be relaxed to n Approximate knowledge of ( most 1 ± … Multiplication error ) , Without affecting our results .
We define the competitiveness of online algorithms as follows : Definition 1. Make OPT Indicates an offline problem (1) The optimal target value of . If you use A The expected value of the obtained online solution is at least that of the optimal offline solution c factor , Online algorithm A It is competitive in the random replacement model . That is ,
()
among , Expectation comes from 110 0 01 n Uniform random arrangement of ,xt It's an algorithm A The second... When the input arrives in sequence t A decision .
In this paper , In the above two assumptions and b Under the lower bound condition of size , Online linear programming is proposed (2) The approximate optimal algorithm . We also extend our results to the following more general online linear optimization problems , Have multidimensional decisions in each time period :
• Consider a range of n A nonnegative vector f1 1f2 1 0 0 0 1fn ∈ k ,mn A nonnegative vector
gi1 1 gi2 1 0 0 0 1 gin ∈ 601 17 k 1 i = 11 0 0 0 1 m
and K = 8x ∈ k 2 x T e ¶ 11 x ¾ 09( We use e Express all 1 Vector ). Offline linear programming is an option x1 10 0 01 xn To solve
()
In the corresponding online question , Given the previous t −1 A decision x1 10 0 01 xt−1 , Every time we choose one k Dimensional decision xt ∈ k , Satisfy
(3)
Use time t Knowledge . The goal is to maximize... Over the entire time frame Pn j=1 f T j xj. Please note that , problem (2) Is the problem (3) The special case of , among k = 1.
1.1. Specific application
below , We will show online LP Some specific applications of the model . These examples are only a small part of the wide application of the model .
1.1.1 Online backpack / Secretary question . This paper studies the online LP A one-dimensional version of the problem is often referred to as an online backpack or secretary problem . In this kind of problem , Decision makers face a range of options , Each option has a certain cost and value , He must select a subset of them online , To maximize total value without violating cost constraints . The application of this problem occurs in many cases , For example, hiring workers 、 Arrange work and bid in Sponsored Search Auctions .
Random permutation model has been widely used in the study of this problem ( See Kleinberg 2005、Babaioff wait forsomeone 2007 And subsequent references ). In these papers , Or get a constant competition ratio for a finite size problem , Or propose a near optimal algorithm for large problems . In this paper , We studied extending this problem to a higher dimension , A near optimal algorithm is proposed .
1.1.2 Online Routing Problem . Consider a reason for m A computer network connected by strips ; Every side i Have a bounded capacity ( bandwidth ) bi . There are a lot of requests arriving online , Every request requires that the network ∈ m Some capacity at , And the utility or price of the request .
The decision maker's offline problem is given by the following integer program :
()
Can be in Buchbinder and Naor (2009b)、Awerbuch A discussion of this problem can be found in . (1993), And the references . Please note that , This problem is also studied in the name of online packaging .
1.1.3
On-line Adwords problem . Selling online advertising has always been Google 、 The main source of revenue for many Internet companies, such as Yahoo . therefore , Improving the performance of ad distribution systems has become extremely important for these companies , Therefore, it has been paid great attention by the research community in the past Decade .
In the literature , Most studies use online matching models , for example , See Mehta wait forsomeone . (2005)、Goel and Mehta (2008)、Devanur and Hayes (2009)、Karande wait forsomeone . (2011)、Bahmani and Kapralov (2010)、Mahdian and Yan (2011)、Feldman wait forsomeone . (2010, 2009b) and Feldman wait forsomeone . (2009a). In such a model , Yes n Online search queries and m Bidders ( advertiser ), Each bidder ( advertiser ) Have a daily budget bi. According to the relevance of each search keyword , The first i Bidders will query j Offer a certain price ij, To display their ads with search results .3 For the first j A query , Decision makers ( Search engine ) must Select a m Dimension vector xj = 8xij9 m i=1 , among xij ∈ 801 19 It means the first one j Whether the query is assigned to the i Bidders . The corresponding offline problem can be expressed as :
(4)
(4) Of LP Relaxation is generally online LP problem (3) A special case of , among fj = Ïj , gij = ijei among ei It's in addition to the third i One item 1 Of all zeros except i A unit vector .
In the literature , The random permutation hypothesis has recently aroused great interest because of its ease of handling and versatility . Constant competition algorithm and near optimal algorithm have been proposed . We will be in §1.3 For a more comprehensive review .
1.2 Key ideas and main results
The main contribution of this paper is to propose a method to solve the online problem with near optimal competition ratio under the random permutation model LP The algorithm of the problem . Our algorithm is based on the following observations : The optimal solution of offline linear program x ∗ To a large extent, the optimal dual solution p ∗ ∈ m determine , Corresponding to m Two inequality constraints . The optimal dual solution is used as the threshold price , bring x ∗ j > 0 Only when the j ¾ p ∗T aj when . Our online algorithm works by learning the threshold price vector from some initial inputs . Then use the price vector to determine the later decision . However , Our algorithm does not just calculate the price vector once , But wait until …n Step or arrive , Then calculate a new price vector each time the history doubles , That is, in time …n1 2…n1 4…n10 0 0 wait . We show that , Under the size condition entered on the right , Our algorithm has 1 - O4…5 Competitiveness . Our main results are accurately expressed as follows : Theorem 1. For any … > 0, Our online algorithm and online linear programming in random permutation model (2) Compared with having 1−O4…5 Competitiveness , For all inputs , bring
(5)
State the theorem 1 Another way of doing this is , Our algorithm has 1 − O4√ mlog n/B5 Competition ratio . We are §3 The theorem is proved in 1. Notice the theorem 1 The conditions in depend on logn, When n When a large , This is far from meeting everyone's needs . Kleinberg (2005) Proved B ¾ 1/…2 Is in B From the Secretary's question 1 − O4…5 Competition is necessary , This is online LP One dimensional counterpart of the problem , all t Of at = 1.
therefore , Theorem 1 Chinese vs …… The dependence of is close to optimal .
In the next Theorem , We prove that any online algorithm depends on m To get a near optimal solution . Its proof will appear in §4.
Theorem 2. For on-line in random permutation model LP problem (2) Any algorithm of , There is an instance where the competition ratio is less than 1 − ì4…5 When
()
Or equivalently , No algorithm can achieve better than 1 − ì4√ logm/B5 Better competition than .
We also extend our results to (3) The more general model introduced in : Theorem 3. For any … > 0, Our algorithm is applicable to the general on-line LP problem (3) have 1 - O4…5 Competitiveness , For all Input , for example :
(6)
Now let's talk about the theorem 1 And Theorem 3 The conditions in . First , The condition depends only on the right input bi And with OPT Is independent of the size or target coefficient . And through the random arrangement model , They are also independent of the distribution of input data . In this sense , Our results are very robust in terms of the uncertainty of the input data . especially , One advantage of our results is that the conditions are checkable before the algorithm is implemented , This is related to OPT Or different conditions in terms of target coefficient . Even if it's just bi for , Such as the theorem 2 Shown , Yes … The dependency is already optimal , And right m It is necessary to rely on .
about n Dependence , We just need B The order of is log n, Far less than the total number of bids n.
actually , For some small problems , The conditions can be very strict .
however , If the budget is too small , It's not hard to imagine that no online algorithm can do well . contrary , In applications with a large amount of input ( For example, in the online advertising word problem , It is estimated that a large search engine can receive billions of searches every day , Even if we focus on specific categories , This number is OK Still millions ) And a fairly large right-hand input ( for example , Advertisers' budgets ), It is not difficult to meet the conditions . Besides , Theorem 1 And Theorem 3 The conditions in are only theoretical results ; Even if the conditions are not met , The performance of our algorithm may still be very good ( Such as Wang 2012 Some numerical tests in ). therefore , Our results have theoretical and practical significance .
Last , We conclude this section with the following inferences : inference 1. Online LP problem (2) and (3) in , If the maximum entrance of the constraint coefficient is not equal to 1, So our theorem 1 and 3 Still established , Yes Conditions (5) and (6) Replace with
()
among , For each line i,a¯i = maxj 8aij9 in (2), or a¯i = maxj 8gij^9 in (3).
1.3 Related work
The design and analysis of on-line algorithms has always been the focus of computer science 、 It is a topic of wide concern in the field of operations research and management science . lately , Random permutation models are becoming more and more popular , Because it avoids the pessimistic lower bound of antagonistic input model , While still capturing the input uncertainty . Various online algorithms are studied under this model , Including secretarial questions (Kleinberg 2005, Babaioff et al. 2008)、 Online matching and adwords problem (Devanur and Hayes 2009, Feldman et al. 2009a, Goel and Mehta 2008, Mahdian and yan 2011,Karande wait forsomeone .
2011, Bahmani and Kapralov 2010) And online packaging (Feldman et al. 2010, Molinaro and Ravi 2014).
In this work , Two types of results were obtained : A constant competition ratio independent of input parameters is realized ; The other focuses on the performance of the algorithm when the input is large . Our papers fall into the second category . In the following literature review , We will focus on this kind of work .
The first result to achieve near optimal performance in a random permutation model is by Kleinberg (2005) Proposed , For the problem of one-dimensional multi choice of secretaries 1 − O41/ √ B5 Competitive algorithm .
The author also proves that his algorithm achieves 1 − O41/ √ B5 The competition ratio is the best for this problem .
Our results extend his work to competitive 1−O4√ mlog n/B5 Multidimensional cases of . Although the problems look similar , But because it is multidimensional , Our analysis requires different algorithms and different techniques . say concretely ,Kleinberg (2005) The random version of classical secretarial algorithm is recursively applied , At the same time, according to LP Duality theory maintains the price , And has a fixed price update schedule . We also prove that , For multidimensional problems , No online algorithm can achieve better results than 1 − ì4√ logm/B5 Better competition than . As far as we know , This is the first indication that the dependent dimension m The result of the necessity of , In order to achieve the best competitive rate of the problem .
It clearly points out , The high dimension does increase the difficulty of this problem .
Devanur and Hayes (2009) A method based on LP To solve the problem of online advertising words . In their approach , They solved a linear program once , And use its dual solution as the threshold price to make future decisions . The authors prove that the competition ratio of their algorithm is 1 - O4 3 p maxm2 log n/OPT5. In our work , We consider a more general model , An algorithm is developed , Update the dual price at a carefully selected rate . By using dynamic updates , Our implementation depends only on B: 1 − O4√ mlog n/B5 The competition ratio . This is very attractive in practice , Because it can be checked before the problem is solved B, and OPT You can't . Besides , We show that our results are correct B The dependency is optimal . Although our algorithm is similar to their idea , But the dynamic characteristics of our algorithm need more detailed design and analysis . We also answered the important question of how often we should update the double price , It is shown that the dynamic learning algorithm can be used for significant improvement .
lately , Feldman et al . (2010) A more general online packaging problem is studied , This problem allows the dimension of the selection set to change in each time period ( Yes (3) Further expansion of ). They proposed a one-time learning algorithm , The implementation of the algorithm depends on the right B and OPT The competition ratio . And right B The dependency of is 1 - O4√3 mlog n/B5. therefore , Compared with their competitive ratio , Our results not only eliminate the right OPT Dependence , And improve the understanding of B Dependence .
table 1
We show that , This improvement is the result of using dynamic learning .
lately ,Molinaro and Ravi (2014) The same problem is studied and 1 − O4p m2 logm/B5 Competition ratio . The main structure of their algorithm ( Especially the way they get the square root instead of the cubic root ) Is modified from this article . They further use a novel coverage technique to eliminate the effect of n Dependence , The price is to increase m The order of magnitude . by comparison , We propose the improvement from cube root to square root and how to eliminate the OPT Dependence .
Kleinberg (2005)、Devanur and Hayes (2009)、Feldman The results of et al . (2010)、Molinaro and Ravi (2014), This work is shown in the table 1 Shown .
Except for the random permutation model ,Devanur wait forsomeone .
(2011) The online resource allocation problem under their so-called antagonistic random input model is studied . The model generalizes from i.i.d Draw Columns . Distribute ; however , It is more rigorous than the random permutation model . especially , Their model does not allow many... To exist in the input sequence “ impact ” The situation of . For this input model , They developed an algorithm , Can achieve 1 − O4max8 √ logm/B1 p max logm/OPT95 The competition ratio . Their results are important , Because it realizes the right m Near optimal dependency of . However , Yes OPT The dependence on and stronger assumptions make it impossible to compare directly with our results , And their algorithm uses a completely different technology from ours .
In operations research and Management Science , Dynamic optimal pricing strategy for various online revenue management and resource allocation problems has always been an important research topic ; Research includes Elmaghraby and Keskinocak (2003)、Gallego and van Ryzin (1997, 1994)、Talluri and van Ryzin (1998)、Cooper (2002) as well as Bitran and Caldentey (2003). stay Gallego and van Ryzin (1997, 1994) as well as Bitran and Caldentey (2003) in , The arrival process is considered price sensitive . However , just as Cooper (2002) Comment on , This model can be simplified as a price independent arrival process , Availability control under Poisson arrival . Our model can be further considered as a discrete version of the availability control model , The model is also used as Talluri and van Ryzin (1998) The basic model of , And in Cooper (2002) It is discussed in . Use the idea threshold or “ offer ” The price is not new . It consists of Williamson (1992) and Simpson (1989) Put forward , And in Talluri and van Ryzin (1998) To further study . stay Talluri and van Ryzin (1998) in , The author shows that the bidding price control policy is asymptotically optimal . However , They assumed knowledge of the arrival process , So prices are calculated by using distribution information “ forecast ” The future, not from the observation of the past as we have done in the paper “ Study ” To get . Cooper (2002) The use of LP The idea of finding a double optimal bid price , Asymptotic optimization is also achieved . But the same , Suppose the arrival process is known , This makes the analysis completely different .
This paper has made contributions in several aspects . First , We studied a general online LP frame , It extends the scope of many previous work . And because of its dynamic learning ability , Our algorithm is non distributed —— In addition to the random arrival order and the total number of entries , Assume no knowledge of the input distribution . Besides , We don't just learn about price once , Instead, a dynamic learning algorithm is proposed , Prices can be updated as more information is disclosed . The design of this algorithm answers Cooper (2002) Questions raised , That is, how long and when prices should be updated ? We prove that at geometric intervals ( Not too often, not too often ) The updated price is the best , This clearly answers the question . therefore , We propose an accurate quantitative dynamic price update strategy . Besides , We provide an important lower bound for this problem , This is the first of its kind , It shows that the dimension of the problem increases its difficulty
In our analysis , We apply many standard techniques that may approximate correct learning , In particular, focus on scope and coverage arguments . Our dynamic learning and learning problems are used in “ Double skill ” Have similar ideas . However , Different from the doubling technique usually applied to unknown time ranges (Cesa-Bianchi and Lugosi 2006), We show that , Updating prices at geometric speeds over a well-designed fixed time frame can also improve performance Algorithm .
1.4 The structure of the paper
The rest of this paper is arranged as follows . stay §§2 and 3 in , We show our online algorithm , And it is proved that it can achieve 1−O4…5 Competition ratio .
To make the discussion clear , We started from 2 Section starts with a simpler one-time learning algorithm . Although the analysis of this simpler algorithm will help to demonstrate our proof technique , However, the results obtained in this setting are weaker than those obtained by our dynamic learning algorithm , This is in the 3 Discussed in Section . In the 4 In the festival , We give a theorem 2 Detailed proof of , On the necessity of using lower bound conditions in our main theorems . In the 5 In the festival , We introduced several extensions of our research . We are the first 6 It is concluded in this section that
2 One time learning algorithm
In this section , We propose a method for online LP A one-time learning algorithm for the problem (OLA). We consider the following partial linear programming , Define only on input until time s = …n( For the convenience of expressing , Without losing generality , We assume that …n It is an integer in the whole analysis process ):
(7)
(8)
Make 4p^1 y^5 by (8) The best solution . Please note that ,p^ It has the natural meaning of the price of each resource . For any given price vector p, We define allocation rules xt 4p5 as follows :
(9)
We now state our OLA:
Algorithm OLA( One time learning algorithm )
1 initialization xt = 0, For all t ¶ s. p^ As defined above .
2 about t = s +11 s +210 0 01 n, If aitxt 4p^5 ¶ bi − Pt−1 j=1 aijxj For all i, set up xt = xt 4p^5; otherwise , Set up xt = 0. Output xt .
stay OLA in , Before we use …n Arrival to learn the dual price vector . then , In every time t > …n when , As long as it does not violate any constraints , We use this dual price to determine the current allocation and implement this decision . An attractive feature of this algorithm is that it requires us to solve only one problem defined in …n Small linear programs on variables . Please note that ,(7) The right side of is factored 1 - … modify .
This modification ensures that the distribution xt 4p5 Probably won't break the constraint . This technique is also used in 3 In the festival , We study dynamic learning algorithms . In the next section , We certify that the following is about OLA The proposition of competitive ratio of , It depends on the ratio theorem 1 Stronger conditions : proposition 1. For any … > 0,OLA yes 1−6… For online linear programming (2 ) In the random displacement model , For all inputs , bring
()
2.1 Competitive ratio analysis
Observe OLA Wait until the time s = …n, Then time t The solution of is set to xt 4p^5, Unless it violates the constraint . To prove its competitiveness , We follow the following steps . First , We prove that if p ∗ yes (1) The optimal dual solution of , be 8xt 4p ∗ 59 Close to the original optimal solution x ∗ ; namely , Learning the dual price is sufficient to determine a close primal solution . However , Because these columns are displayed online , We cannot obtain... During the decision-making period p*. contrary , In our algorithm , We use p^ As a substitute . Then we prove p^ yes p ∗ A good substitute for : (1) Is likely to ,xt 4p^5 Satisfy all constraints of linear programming ; (2) P t txt 4p^5 The expected value of is close to the optimal off-line value . Before starting the analysis , We made the following simplified technical assumptions in the discussion : hypothesis 3. The problem input is in the general position —— namely , For any price vector p—— Up to m Columns make p T at = Tons of .
hypothesis 3 Not necessarily for all inputs . However , just as Devanur and Hayes (2009) Pointed out , People can always add a random variable Žt In the interval 601 ‡7 Random disturbance by uniform distribution t Any small amount ‡. such , When the probability is 1 Under the circumstances , stay p T at = t in , No, p Can satisfy at the same time m + 1 An equation , And the influence of this disturbance on the target can be arbitrarily small . Under this assumption , We can use linear programming (1) To obtain the following lemma .
lemma 1. xt 4p * 5 ¶ x * t For all t, And assuming 3 Next ,x * t and xt 4p * 5 The difference is no more than m individual t value .
prove . Consider offline linear programming (1) And its duality ( Make p Represents the dual variables associated with the first set of constraints ,yt Representations and constraints xt ¶ 1 Related dual variables ):
(10)
According to the complementary relaxation condition , For the original question (1) Any optimal solution of x ∗ And the optimal solution of duality 4p ∗ 1 y ∗ 5, We must have :
()
If xt 4p * 5 = 1, adopt (9),t > 4p * 5 T at . therefore , adopt (10) Constraints in ,y * t > 0, Last , Through the final complementary condition ,x * t = 1. therefore , For all t, We have xt 4p * 5 ¶ x * t.
however , If t < 4p ∗ 5 T at , Then we must have at the same time xt 4p ∗ 5 and x ∗ t = 0. therefore , If 4p ∗ 5 T at 6= t , be xt 4p ∗ 5 = x ∗ t . Assuming 3 Next , At most m individual t value , bring 4p ∗ 5 T at = t . therefore ,x * t and xt 4p * 5 The difference is no more than m individual t value . ƒ lemma 1 indicate , If the optimal dual solution is known p * To (1), Through our decision-making strategy xt 4p * 5 Near optimal off-line solution . However , In our online algorithm , We use the sample dual price learned from the previous inputs p^, This may be related to the optimal dual price p∗ Different .
The remaining discussion attempts to show that the sample dual price p It is accurate enough for our purpose .
In the following , We often use the fact that , That is to say, the random order hypothesis can be interpreted as the former s The first input is a uniform random sample , And not from n Replace size in input s. We use it S The size is s Sample set , use N The size is n Complete input set for . We start with lemma 2 Start , This shows that the primal solution constructed by using the sample dual price xt 4p^5 It is likely to be feasible : lemma 2. The original solution constructed by using sample dual price is linear programming (1) Feasible solution of The probability is high . More precisely , The probability of 1 - …,
()
Given B ¾ 6mlog4n/…5/…3.
prove . Consider any fixed price p and i. If and only if p It's a sample set S Of (8) Optimal dual price of , but Pn t=1 aitxt 4p5 > bi when , We say sample S Yes p and i yes “ Bad ”.
First , We show that for each fixed p and i, The probability of a bad sample is very small . Then we make a joint constraint on all the different prices , To prove the learned price p^ It is likely to make Pn t=1 aitxt 4p^5 ¶ bi For all i.
First , We fix p and i. Definition Yt = aitxt 4p5. If p yes S The optimal dual solution of a linear program with upper samples , General lemma 1 Applied to sample problems , We have
()
among x yes S The original optimal solution of the sample linear program on . Now let's consider this p and i The probability of a bad sample :
()
Besides , We have
()
among „ = …/4m · n m5. The penultimate step follows Hoeffding-Bernstein The sampling inequality without putting back ( appendix A The lemma in 10), take Zt , t ∈ S Deemed to come from Zt , t ∈ N No return sample of .
We also used 0 ¶ Zt ¶ 1 For all t Fact ; therefore ,P t∈N 4Zt − Z¯5 2 ¶ P t∈N Z 2 t ¶ bi ( So lemma 10 Medium ‘ 2 R Can be bi Definition ). Last , The last inequality is due to B Assumptions made .
Next , We are interested in all the different p Make joint constraints . We call two price vectors p and q Different if and only if they produce different solutions ; namely ,8xt 4p59 6= 8xt 4q59. Please note that , We just need to consider different prices , Otherwise all Yt It's all the same . Please note that , Each is different p Is characterized by m+1 In dimensional space n A little bit ( stay 9 n t=1 Place for 8 t 1 ) The only separation . According to the results of computational geometry , The maximum total number of such different prices is n m(Orlik and Terao 1992). Yes n m A combination of different prices , also i = 110 0 01 m, We got the result we wanted . ƒ We show that ,xt 4p^5 It is likely to be a viable solution . In the following , We will prove that it is also a near optimal solution .
lemma 3. The original solution constructed by using sample dual price is linear programming (1) High probability approximate optimal solution . More precisely , The probability of 1 - …,
()
Given B ¾ 6mlog4n/…5/…3.
prove . The proof is based on two observations . First ,8xt 4p^59n t=1 and p^ All complementary conditions are met , Therefore, it is the optimal primal and dual solution of the following linear programming :
(11)
among b^ i = P t∈N aitxt 4p^5 stay p^i > 0 Under the circumstances ,b^ i = max8 P t∈N aitxt 4p^51 bi 9, If p^i = 0.
secondly , We prove that if p^i > 0, Then the probability is 1−…, b^ i ¾ 41−3…5bi . To prove it , set up p^ Is a collection S Optimal dual solution of sample linear program on ,x^ Is the optimal primitive solution . By the complementary condition of linear programming , If p^i > 0, Is the first i Constraints must be equal . in other words ,P t∈S aitx^t = 41−…5…bi . then , Through lemma 1 and B = mini bi ¾ m/… 2 Conditions , We have
()
then , Use Hoeffding-Bernstein Inequality for sampling without putting back , In a way similar to lemma 2 The way of proof , We can prove that ( The details are shown in Appendix A.2 Give in ), Given B Lower bound of , There is a probability At least 1 - …, For all i bring p^i > 0:
(12)
combination p^i = 0 The situation of , We know all i The probability of is 1−…, b^ i ¾ 41−3…5bi. Last , It is observed that as long as (12) establish , Given (1) The best solution x ∗,41 - 3…5x ∗ It will be (11) Feasible solution of . therefore ,(11) The optimal value of is at least 41 − 3…5OPT, It's equivalent to saying
()
therefore , The target value of the online solution adopted in the whole cycle is close to the optimal value . However , stay OLA in , In the learning cycle S No decision was made during the period , Only from the cycle 8s + 110 0 01 n9 The decision of contributes to the target value . The following lemma will sample the linear program (7) The optimal value of and offline linear program (1) The optimal value of , Will limit the contribution of the study period : lemma 4. Make OPT4S5 Express sample S Linear program on (7) and OPT4N 5 Express N Offline linear program on (1) The optimal value .
then ,
()
prove . Make 4x ∗ 1p ∗ 1 y ∗ 5 and 4x1p1 y^5 respectively N Linear program on (1) and S Sample linear program on (7) The optimal primal solution and dual solution of .
()
Be careful S ⊆ N, therefore 4p ∗ 1 y ∗ 5 yes S The dual feasible solution of linear programming on . therefore , By the weak duality theorem :
()
Now? , We are going to prove the proposition 1: proposition 1 The proof of . Using lemmas 2 and 3, The probability is at least 1 − 2…, The following events occurred :
()
in other words , Decision making xt 4p^5 It is feasible. , And throughout the cycle 8110 0 01 n9 The target value adopted on is close to the optimal value .
use E This is an event , among P 4E5 ¾ 1 − 2…. We have lemmas 2-4: ()
among I4·5 Is an indicator function , The first inequality is because in E Next ,xt = xt 4p^5, The penultimate inequality uses xt 4p^5 ¶ x^t Fact , This is lemma 1 Result
3 Dynamic learning algorithm
§2 Before using the algorithm discussed in …n Input to learn the threshold price , Then apply it to the remaining time range . Although the algorithm has its own advantages —— especially , It only needs to solve a definition in …n Small linear programs on variables ——B The required lower bound ratio theorem 1 The lower limit declared in is strong … factor .
In this section , We propose an improved dynamic learning algorithm (DLA), It will implement the theorem 1 Results in .
DLA Not just once , Instead, prices are updated every time history doubles , in other words , It will be in time t = …n1 2…n1 4…n10 0 0 Learn a new price . To be exact , Give Way p^ Represents the optimal dual solution of the following partial linear programs defined on the input , Until time
()
Where the number set h The definition is as follows :
()
Besides , For any given dual price vector p, We define and (9) The same allocation rules in xt 4p5. Our dynamic learning algorithm is as follows :
Algorithm DLA( Dynamic learning algorithm )
1 initialization t0 = …n. For all t ¶ t0 Set up xt = 0.
2 repeat t = t0 + 11 t0 + 21 0 0 0 (a) Set up x^t = xt 4p^ 5. here = 2 r …n among r Is the largest integer such that < t
3 (b) If aitx^t ¶ bi − Pt−1 j=1 aijxj For all i, Then set xt = x^t ; otherwise , Set up xt = 0. Output xt .
Please note that , We have updated the dual price vector over the entire time horizon “log2 41/…5” Time . therefore ,DLA More calculations are needed . However , As we will show next , It needs to B To prove the same competitive ratio . The intuition behind this improvement is as follows .
first , stay = …n,h = √ … > …. therefore , We have a lot of slack at the beginning , And the constraint satisfies the large deviation parameter ( Such as lemma 2) need B The weaker condition on . With t increase , Increase and h Reduce .
however , For the larger value , The sample size is large , bring B The weak condition on is sufficient to prove the same error bounds . Besides ,h Fall fast enough , Therefore, the overall loss of the target value is not significant .
As people will see , Choose the numbers carefully h It plays an important role in proving our results .
3.1 Competitive ratio analysis
DLA The analysis of OLA In a similar way . However , It is necessary to prove the stronger results of the learned prices in each period . In the following , We assume that … = 2 -E And let L = 8…n1 2…n1 0 0 0 1 2 E-1 …n9.
lemma 5 and 6 And §2 The lemma in 2 and 3 parallel , But you need B The weaker condition on : lemma 5. For any … > 0, The probability of 1 - …:
()
Given B = mini bi ¾ 410mlog 4n/…55/…2.
prove . Proof is similar to lemma 2 The proof of , But more careful analysis is needed . We provide a brief outline here , And in the appendix B.1 Provide detailed proof in . First , We fix p、i and . This time, , If and only if p = p^ ( namely p Is the learning price under the current arrival order ) but P2 t=+1 aitxt 4p^ 5 > 4/n5bi . By using Hoeffding-Bernstein Inequality for sampling without putting back , We proved that in B Under the condition of , For any fixed p、i and ,“ bad ” The probability of permutation is less than „ = …/4m·n·m·E5. And then by taking The union binds all different prices , All items i And period , Lemma is proved . ƒ In the following , We use LPs 4d5 Indicates that it is set to in the inequality constraint d Until time s The variables defined on the partial linear programming . That is ,
()
And let OPTs 4d5 Express LPs 4d5 The best target value for .
lemma 6. For all ∈ L, The probability is at least 1 - …:
()
Given B = mini bi ¾ 410mlog 4n/…55/…2.
prove . Make b^ i = P2j=1 aijxj 4p^ 5 about i bring p^ i > 0, also b^ i = max8 P2 j=1 aijxj 4p^ 51 4425/n5bi 9, otherwise . So the solution is right 48xt 4p^ 592 t=1 1 p^ 5 All complementary conditions are met ; therefore , They are linear programming LP2 4b^5 The best solution ( They are the original solution and the dual solution ):
()
This means
()
Now let's analyze the ratio b^i/42bi/n5. according to b^ i The definition of , about i bring p^ i = 0,b^ i ¾ 2bi/n. otherwise , Use something similar to lemma 5 Proven technology , We can use probability 1 - … prove , For all i,
(14)
(14) See the appendix for the detailed certificate of B.2. Lemma comes from (14). ƒ Next , And lemma 4 similar , We prove that the following lemma relates the optimal value of the sample linear program to the optimal value of the offline linear program : lemma 7. For any
()
lemma 7 Proof and lemma of 4 The proof of is exactly the same ; therefore , We omit its proof .
Now we are ready to prove the theorem 1.
Theorem proving 1. Observe the online solution in time t ∈ 8 + 110 0 01 29 The output of is xt 4p^ ` 5, As long as the constraints are not violated . According to lemma 5 and 6, The probability is at least 1 − 2…:
()
use E This is an event , among P 4E5 ¾ 1 − 2…. The expected target value achieved by the online algorithm can be limited as follows :
()
The third inequality comes from lemma 6; Penultimate inequality comes from lemma 7; The last inequality stems from the fact that :
()
4 Worst case limits for all algorithms
In this section , We prove the theorem 2; namely , Conditions B ¾ ì4logm/…2 5 Is any online algorithm implementation 1 − O4…5 Required for the competitive ratio of . We're building (1) To prove this point , It includes m Projects and... For each project B A unit , So that there is no Online algorithms can be implemented 1 − O4…5 Competition ratio , Unless B ¾ ì4logm/…2 5.
In this construction , We will 0-1 vector at This is called the demand vector , take t It is called profit coefficient . Suppose an integer z Of m = 2 z. We will construct z For demand vectors , Make the requirement vectors in each pair complement each other and do not share any projects .
However , Each group consists of one vector in each pair z Vectors will share at least one common item .
So , Please consider it 2z Possible lengths are z Boolean string of . The first j A Boolean string represents j = 110 0 01 m = 2 z Of the j A project ( For illustrative purposes , We will start from the following discussion 0 Start indexing items ). Give Way sij It means the first one j The first... Of a string i The value of a . Then we construct a pair of demand vectors vi 1wi ∈ 801 19 m, By setting vij = sij, wij = 1 - sij.
surface 2 Illustrates the m = 8 (z = 3) This kind of structure : Notice the vector vi 1wi 1 i = 110 0 01 z It's complementary . Consider for each i = 110 0 01 z Select two vectors vi and wi Any of the z Set of demand vectors . And then by setting sij = 1 If this set has vectors vi and 0 If it has a vector wi To form a bit string . Then all vectors in this collection share the items corresponding to the Boolean string . for example , In the table 2 in , Demand vector v3、w2 and w1 Sharing Project 44=“100”5, Demand vector w3、v2 and v1 Sharing Project 34=“011”5, And so on .
Now? , We built an example , The example consists of a profit coefficient of 4 Of B/z Input and demand vectors vi form , Every i = 11 0 0 0 1 z.
• qi Input , Profit is 3 And demand vector wi , For each i, among qi It's binomial (2B/z1 1/2) Then the random variable .
• √ B/4z Input , Profit is 2, The demand vector is wi, For each i.
• 2B/z - qi Input , Profit is 1, The demand vector is wi, For each i.
Use the attributes of the requirement vector ensured in the construct , We prove the following claim :
table 2
Claims 1. Make ri Represents any of the construction examples 1-… The type of competitive solution accepted is wi The number of vectors of . that , It must hold
()
prove . Make OPT Represents the optimal value of the offline problem . And let OPTi Says from the first i The profit from the demand accepted by the class . Make topwi 4k5 Before presentation k Input and demand vectors wi The sum of the profits . then
()
Make OPT d The acceptance type is wi Of ri The target value of the solution of the vector . First , Please note that P i ri ¶ B. This is because of all wi Share a public project , And the project has at most B Units available . Make Y by 8i2 ri > B/z9 Set , X For the rest of i; namely ,X = 8i 2 ri ¶ B/z9. then , We certify acceptance of vi s The total cannot exceed B - P i∈Y ri + Y B/z. obviously , aggregate Y Your contribution cannot exceed Y B/z vi s. Give Way S ⊆ X Contribute the rest vi. Now consider the set Y All in wi And collection S All in wi Shared projects ( By constructing at least one such project ). Because the project only has B Units available , therefore S Contributing vi The total cannot exceed B − P i∈Y ri . therefore , Accepted vi s The quantity of is less than or equal to B - P i∈Y ri + Y B/z.
Express P = P i∈Y ri -Y B/z,M = XB/z− P i∈X ri . then P 1M ¾ 0 And target value
()
because OPT ¶ 7B, It means P +M Must be less than 7…B In order to obtain 1 - … Or a better approximation than . ƒ Here is a brief description of the remainder proof . By construction , For each i, There happens to be 2B/z Demand vectors wi, Its profit coefficient is 1 and 3; among , Each value 1 or 3 The probability is equal . Judging from the previous propositions , To get a near optimal solution , Must choose wi The proximity of the type B/z Demand vector . therefore , If 431wi 5 The total number of entries is greater than B/z, Then choose any 421wi 5 Will result in a loss of profit compared to the optimal profit 1; If 431wi 5 The total number entered is less than B/z - √ B/4z, Reject any 421wi 5 Will result in loss of profits 1. Using the central limit theorem , At any step , Both events can occur with a constant probability . therefore , about 421wi 5 Every decision of may lead to a loss with a constant probability , This leads to every i The total expected loss of is ì4√ B/z5, The total loss is ì4√ zB5.
If you want to accept wi The number of is not exactly B/z, Then these √ B/z Some of the decisions may not be wrong , But as the above claims , This cannot exceed 7…B.
therefore , The expectation for online solutions is ONLINE ¶ OPT - ì4√ zB - 7…B50 because OPT ¶ 7B, To get 41 - …5 Approximation factor , We need to ì4p z/B - 7…5 ¶ 7… ⇒ B ¾ ì4z/…2 5 = ì4log4m5/…2 50 This completes the theorem 2 The proof of . A detailed description of the steps used in this certification is given in Appendix C.
5 Expand
5.1 Online multidimensional linear programming
We consider the following more general online linear programs , There are multidimensional decisions in each step xt ∈ k, Such as §1 Medium (3) As defined in :
(15)
Our online algorithm remains basically unchanged ( Such as §3 Described in ), Now it is defined as follows xt 4p5:
()
here er It's the unit vector , In the r Entries are 1, Otherwise 0. We arbitrarily break the relationship in the algorithm . Use (15) Conditions and theorems of complementarity 3 Assumed in B The lower bound condition of , We can prove the following lemma . 4 The proof is very similar to the one-dimensional case , And in the appendix D Provided in the .
lemma 8. Make x ∗ and p ∗ Namely (15) The optimal primal solution and dual solution of . that x ∗ t and xt 4p ∗ 5 At most m individual t Values are different .
lemma 9. If and only if xt 4p5 6= xt 4q5 For a t when , Definition p and q Is different . So at most n mk 2m Different price vectors .
With the above lemma , Theorem 3 The proof of will be related to the theorem 1 The proof of is exactly the same .
5.2 Online integer programming
according to (9) in xt 4p5 The definition of , Our algorithm always outputs integer solutions . Since the competitive ratio analysis will be solved online with the corresponding LP The optimal solution of relaxation is compared , So theorem 1 The competitive ratio in is also applicable to online integer programming . §5.1 The general online linear program described in has the same observations , Because it also outputs integer solutions
5.3 Fast solution of large linear programs by column sampling
In addition to online questions , Our algorithm can also be applied to solve ( offline ) Linear programs are too large to explicitly consider all variables . Similar to a one-time online learning solution , Can be randomly selected …n A variable , And use the dual solution of this smaller program p^ Put the variable xj Is set to xj 4p^5. This method is very similar to the column generation method used to solve large linear programs (Dantzig 1963). Our results are the first to rigorously analyze the approximation achieved by randomly selecting subsets of columns to reduce the size of linear programs .
6 Conclusion
In this paper , We assume some mild conditions of random arrival order and right-hand input , For general categories of online LP The question provides a kind of 1−O4…5 Competitive algorithm . We use conditions with optimal target values 、 The target coefficient is independent of the distribution of the input data .
our DLA It works by dynamically updating the threshold price vector at geometric intervals , The double price learned from the column displayed in the previous period is used to determine the sequence decision of the current period . Our dynamic learning method may help to design online algorithms for other problems .
There are still many problems in future research . An important issue is the current right-hand input B Whether the size limit is strict . As we have shown , There is a gap between our algorithm and the lower bound . Through some numerical experiments , We find that the actual performance of our algorithm is close to the lower bound ( see Wang 2012). however , We cannot prove this . Filling this gap will be a very interesting direction for future research .
边栏推荐
- 【深入理解TcaplusDB技术】单据受理之建表审批
- Dynamicdatabasesource, which supports the master-slave database on the application side
- [proteus simulation] H-bridge drive DC motor composed of triode + key forward and reverse control
- Redis持久化的几种方式——深入解析RDB
- MYSQL 几个常用命令使用
- Redis中的Multi事务
- Async-profiler介绍
- 一个支持IPFS的电子邮件——SKIFF
- 【深入理解TcaplusDB技术】TcaplusDB运维
- Stochastic Adaptive Dynamics of a Simple Market as a Non-Stationary Multi-Armed Bandit Problem
猜你喜欢

MySQL foundation - constraints

Please describe the whole process from entering a URL in the browser to rendering the page.

How to realize @ person function in IM instant messaging

运用span-method巧妙实现多层table数据的行合并

He was in '98. I can't play with him

Introduction to async profiler
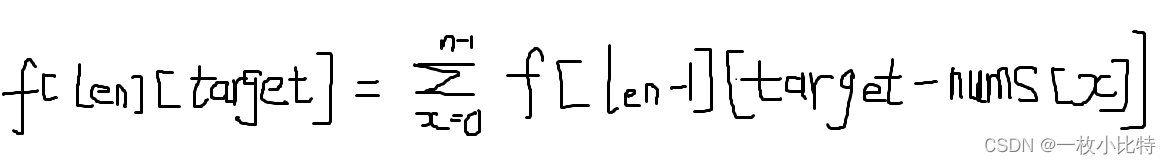
完全背包如何考慮排列問題

Teach you how to create SSM project structure in idea
mysql8.0忘记密码的详细解决方法

从感知机到Transformer,一文概述深度学习简史
随机推荐
JWT简介
web技术分享| 【高德地图】实现自定义的轨迹回放
How should programmers look up dates
【Proteus仿真】8x8Led点阵数字循环显示
Teach you how to create SSM project structure in idea
[deeply understand tcapulusdb technology] tcapulusdb table management - delete table
Lora technology -- Lora signal changes from data to Lora spread spectrum signal, and then from RF signal to data through demodulation
CVPR 2022 Oral | 视频文本预训练新SOTA,港大、腾讯ARC Lab推出基于多项选择题的借口任务
IDEA写jsp代码报错,但是正常运行解决
Shell编程基础(第七篇:分支语句-if)
天,靠八股文逆袭了啊
元宇宙中的云计算,提升你的数字体验
leetcode.11 --- 盛最多水的容器
What can the accelerated implementation of digital economy bring to SMEs?
R语言data.table导入数据实战:data.table数据列名称的重命名(rename)
[resolved] -go_ out: protoc-gen-go: Plugin failed with status code 1.
MySQL基础——函数
[deeply understand tcapulusdb technology] create a game area for document acceptance
软件压力测试有哪些方法,如何选择软件压力测试机构?
[proteus simulation] NE555 delay circuit
